[CodeForce431C]k-tree

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a \(k\) -tree.

最近有一个富有创造力的学生Lesha听了一个关于树的讲座。在听完讲座之后，Lesha受到了启发，并且他有一个关于k-tree（k叉树）的想法。

A k -tree is an infinite rooted tree where:

each vertex has exactly k k children;

each edge has some weight;

if we look at the edges that goes from some vertex to its children (exactly k k edges), then their weights will equal\(1,2,3,...,k\).

k-tree都是无根树，并且满足：

每一个非叶子节点都有k个孩子节点；

每一条边都有一个边权；

每一个非叶子节点指向其k个孩子节点的k条边的权值分别为1,2,3,...,k。

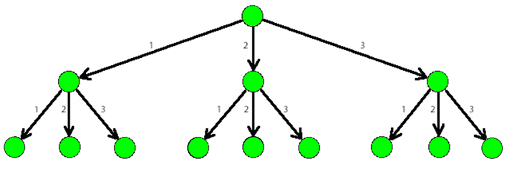
The picture below shows a part of a 3-tree.

如图所示：

As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight n n (the sum of all weights of the edges in the path) are there, starting from the root of a k k -tree and also containing at least one edge of weight at least d d ?".Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 1000000007 (\(10^{9}+7\)).

当Lesha的好朋友Dima看到这种树时，Dima马上想到了一个问题：“有多少条从k-tree的根节点出发的路上的边权之和等于n，并且经过的这些边中至少有一条边的边权大于等于d呢?” 现在你需要帮助Dima解决这个问题。考虑到路径总数可能会非常大，所以只需输出路径总数 mod 1000000007 即可。（1000000007=10^9+7）

输入格式

A single line contains three space-separated integers: n, k and d(\(1<=n,k<=100;1<=d<=k\)).

只有一行数，n，k，d. (1 <= n, k <= 100; 1 <= d <= k; n, d, k 三者用空格隔开)。

输出格式

Print a single integer — the answer to the problem modulo1000000007 (\(10^{9}+7\)).

只有一行，一个整数，即输出路径总数 mod 1000000007。

样例输入

3 3 2

样例输出

3

题解

#include<bits/stdc++.h>
#define maxk 105
#define maxn 105
using namespace std;
const long long mod = 1e9+7;
inline char get(){
	static char buf[3000],*p1=buf,*p2=buf;
	return p1==p2 && (p2=(p1=buf)+fread(buf,1,3000,stdin),p1==p2)?EOF:*p1++;
}
inline long long read(){
	register char c=get();register long long f=1,_=0;
	while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
	while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
	return _*f;
}
long long n,k,d;
long long dp[maxn][3];//第一维记录不考虑d的情况，第二维记录考虑d的情况
long long cas;
int main(){
	//freopen("1.txt","r",stdin);
	n=read();k=read();d=read();//总和等于n，k叉树，至少一条边大于等于d
	for(register long long i=1;i<=n;i++){//i表示当前n=i
		for(register long long j=1;j<=k && j<=i;j++){
			cas=i-j;
			bool used_d=0;
			if(j>=d)used_d=1;
			dp[i][1]+=dp[cas][1];//因为第一维不考虑d的大小，直接相加即可
			if(cas==0){
				dp[i][1]++;//无论如何第一维都要加
				if(used_d)dp[i][2]++;//如果当前考虑了d，则让考虑了d的维度更新
			}
			else{
				if(used_d)dp[i][2]+=dp[cas][1];//如果目前考虑的d,则之前就不用考虑d了
				else dp[i][2]+=dp[cas][2];//如果目前没考虑d，则之前要考虑d
			}
		}
		dp[i][1]%=mod;
		dp[i][2]%=mod;
	}
	cout<<dp[n][2]%mod;
	return 0;
}