洛谷P1955 [NOI2015] 程序自动分析 [并查集，离散化]

　　题目传送门

---

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若e=0，则该约束条件为xi≠xj；

输出格式：

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入样例#1：

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例#1：

NO
YES

输入样例#2：

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出样例#2：

YES
NO

说明

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

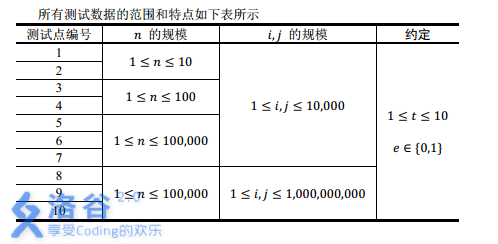
【时限2s，内存512M】

---

　　

　　分析：一眼可知是并查集，问题就在离散化，数据范围肯定不能直接上。但是蒟蒻并不擅长离散化，一开始还好感人地打了个hash，搞了半天结果屏幕上wa声一片……然后翻了翻大佬们的博客，发现。。。模个数就行了（O.o）。。好吧，是我太蒻了。

　　Code：

　　

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<iomanip>
#include<algorithm>
using namespace std;
const int mod=;
const int N=1e5+;
int n,T,cnt,fa[mod+],rank[mod+];
struct Ques{int x,y;}a[N];
inline int read()
{
  char ch=getchar();int num=;bool flag=false;
  while(ch<''||ch>''){if(ch=='-')flag=true;ch=getchar();}
  while(ch>=''&&ch<=''){num=num*+ch-'';ch=getchar();}
  return flag?-num:num;
}
inline void ready()
{
  cnt=;
  for(int i=;i<=mod;i++)fa[i]=i;
  for(int i=;i<=mod;i++)rank[i]=;
}
inline int find(int x)
{return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void merge(int x,int y)
{
  if(rank[x]<rank[y]){
    fa[x]=y;}
  else{
    fa[y]=x;
    if(rank[x]==rank[y])rank[x]++;}
}
inline int work()
{
  for(int i=;i<=n;i++){
    int x=read();int y=read();int e=read();
    x%=mod;y%=mod;
    if(e)merge(find(x),find(y));
    else{a[++cnt].x=x;a[cnt].y=y;}
  }
  bool flag=true;
  for(int i=;i<=cnt;i++)
    if(find(a[i].x)==find(a[i].y))
      {flag=false;break;}
  if(flag)puts("YES");
  else puts("NO");
}
int main()
{
  T=read();
  while(T--){
    n=read();
    ready();work();}
  return ;
}