单源点最短路径的Dijkstra算法
- #include<stdio.h>
- #define MAXSIZE 6
- #define INF 32767
- void Ppath(int path[],int i,int v0)//先序递归查找最短路径(源点为v0)上的顶点
- {
- int k;
- k=path[i];
- if(k!=v0)//顶点Vk不是源点V0时
- {
- Ppath(path,k,v0);//递归查找顶点Vk的前一个顶点
- printf("%d,",k);//输出顶点Vk
- }
- }
- void Dispath(int dist[],int path[],int s[],int v0,int n)//输出最短路径
- {
- int i;
- for(i=;i<n;i++)
- if(s[i]==)//顶点Vi在集合S中
- {
- printf("从%d到%d的最短路径长度为:%d,路径为:",v0,i,dist[i]);
- printf("%d,",v0);//输出路径上的源点v0;
- Ppath(path,i,v0);//输出路径上的中间顶点vi
- printf("%d\n",i);//输出路径上的终点
- }
- else
- printf("从%d到%d不存在路径\n",v0,i);
- }
- void Dijkstra(int gm[][MAXSIZE],int v0,int n)//Dijkstra算法
- {
- int dist[MAXSIZE],path[MAXSIZE],s[MAXSIZE];
- int i,j,k,mindis;
- for(i=;i<n;i++)
- {
- dist[i]=gm[v0][i];//v0到vi的最短路径初值赋给dist[i]
- s[i]=;//s[i]=0表示顶点vi属于T集
- if(gm[v0][i]<INF)//路径初始化,INF为可取的最大常数
- path[i]=v0;
- else
- path[i]=-;//v0到vi没有边
- }
- s[v0]=;path[v0]=;//V0并入集合S且V0当前最短路径中无前一个顶点
- for(i=;i<n;i++)//对除V0外的n-1个顶点寻找最短路径,即循环n-1次
- {
- mindis=INF;
- for(j=;j<n;j++)//从当前集合T中选择一个路径长度最短的顶点Vk
- if(s[j]==&&dist[j]<mindis)
- {
- k=j;
- mindis=dist[j];
- }
- s[k]=;//顶点Vk加入集合S中
- for(j=;j<n;j++)//调整源点v0到集合T中任一顶点Vj的路径长度
- if(s[j]==)//顶点vj在集合T中
- if(gm[k][j]<INF&&dist[k]+gm[k][j]<dist[j])//当V0到Vj的路径长度小于V0到Vk和Vk到Vj的路径长度时
- {
- dist[j]=dist[k]+gm[k][j];
- path[j]=k;//Vk是当前最短路径中Vj的前一个顶点
- }
- }
- Dispath(dist,path,s,v0,n);//输出最短路径
- }
- void main()
- {
- int g[MAXSIZE][MAXSIZE]={{INF,,,INF,INF,INF},{,INF,INF,INF,,},{INF,,INF,INF,INF,},
- {INF,INF,INF,INF,INF,INF},{INF,INF,INF,,INF,INF},{INF,INF,INF,,,INF}};//定义邻接矩阵g
- Dijkstra(g,,);//求顶点0的最短路径
- }
输出: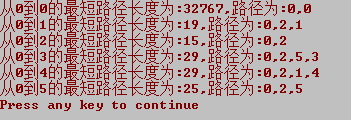
带权有向图及邻接矩阵示意: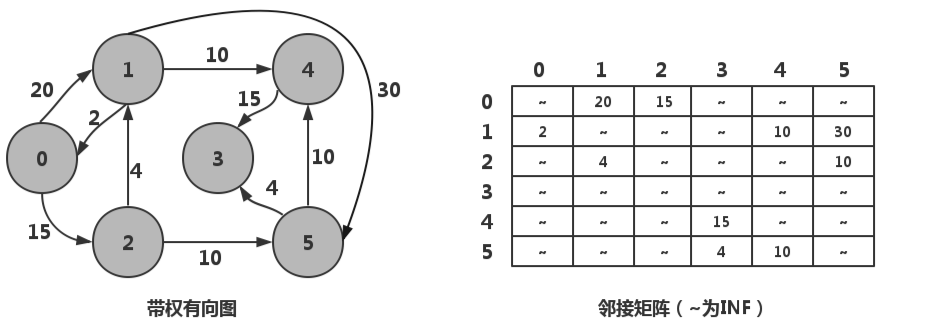
单源点最短路径的Dijkstra算法的更多相关文章
- 单源最短路径(dijkstra算法)php实现
做一个医学项目,当中在病例评分时会用到单源最短路径的算法.单源最短路径的dijkstra算法的思路例如以下: 如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点.那么( ...
- 【算法设计与分析基础】25、单起点最短路径的dijkstra算法
首先看看这换个数据图 邻接矩阵 dijkstra算法的寻找最短路径的核心就是对于这个节点的数据结构的设计 1.节点中保存有已经加入最短路径的集合中到当前节点的最短路径的节点 2.从起点经过或者不经过 ...
- 【算法导论】单源最短路径之Dijkstra算法
Dijkstra算法解决了有向图上带正权值的单源最短路径问题,其运行时间要比Bellman-Ford算法低,但适用范围比Bellman-Ford算法窄. 迪杰斯特拉提出的按路径长度递增次序来产生源点到 ...
- 单源最短路径:Dijkstra算法(堆优化)
前言:趁着对Dijkstra还有点印象,赶快写一篇笔记. 注意:本文章面向已有Dijkstra算法基础的童鞋. 简介 单源最短路径,在我的理解里就是求从一个源点(起点)到其它点的最短路径的长度. 当然 ...
- 单源最短路径问题-Dijkstra算法
同样是层序遍历,在每次迭代中挑出最小的设置为已知 ===================================== 2017年9月18日10:00:03 dijkstra并不是完全的层序遍历 ...
- 0016:单源最短路径(dijkstra算法)
题目链接:https://www.luogu.com.cn/problem/P4779 题目描述:给定一个 n 个点,m 条有向边的带非负权图,计算从 s 出发,到每个点的距离. 这道题就是一个单源最 ...
- 单源最短路径问题(dijkstra算法 及其 优化算法(优先队列实现))
#define _CRT_SECURE_NO_WARNINGS /* 7 10 0 1 5 0 2 2 1 2 4 1 3 2 2 3 6 2 4 10 3 5 1 4 5 3 4 6 5 5 6 9 ...
- Dijkstra单源点最短路径算法
学习参考: Dijkstra算法(单源最短路径) 最短路径—Dijkstra算法和Floyd算法 使用的图结构: 邻接矩阵: -1 20 -1 25 80-1 -1 40 -1 -1-1 -1 -1 ...
- Bellman-Ford & SPFA 算法——求解单源点最短路径问题
Bellman-Ford算法与另一个非常著名的Dijkstra算法一样,用于求解单源点最短路径问题.Bellman-ford算法除了可求解边权均非负的问题外,还可以解决存在负权边的问题(意义是什么,好 ...
随机推荐
- Python学习笔记(Django篇)——3、创建第一个数据库模型
Django里面集成了SQLite的数据库,对于初期研究来说,可以用这个学习. 第一步,创建数据库就涉及到建表等一系列的工作,在此之前,要先在cmd执行一个命令: python manage.py ...
- sql service (case when then else end ..... group by)
1. 原表: courseid coursename score ------------------------------------- 1 java 70 2 oracle 90 3 xml 4 ...
- PowerDesigner逆向生成
人越长大话越少,我们不再说今天受了委屈,不再说谁谁谁不理我了我好难过,不再分享生活中的琐事. 我知道人和人之间没法互相理解,大家都很忙,针也没扎在别人身上. 所以把那些还没说出口的话消化在每一步走过的 ...
- 关于微信内置浏览器安卓端session丢失问题
项目上线测试,发现微信安卓端存在用户登录无法验证session情况, 导致每次接口请求都无法识别,而苹果客户端不会出现此问题,非微信环境打开不会出现此问题,找到一些解决方案做下记录: 方案1: 由于微 ...
- JSP动态合并单元格
<%@ taglib prefix="c" uri="http://java.sun.com/jsp/jstl/core"%> <table ...
- mysql 事务,锁,与四大隔离级别
概念 事务 原子性:事务必须是一个自动工作的单元,要么全部执行,要么全部不执行. 一致性:事务结束的时候,所有的内部数据都是正确的. 隔离性:并发多个事务时,各个事务不干涉内部数据,处理的都是另外一个 ...
- [洛谷P1527] [国家集训队]矩阵乘法
洛谷题目链接:[国家集训队]矩阵乘法 题目背景 原 <补丁VS错误>请前往P2761 题目描述 给你一个N*N的矩阵,不用算矩阵乘法,但是每次询问一个子矩形的第K小数. 输入输出格式 输入 ...
- python字符串内置函数
1.字符串 定义:它是一个有序的字符的集合,用于存储和表示基本的文本信息,‘’或“”或‘’‘ ’‘’中间包含的内容称之为字符串特性:1.只能存放一个值2.不可变3.按照从左到右的顺序定义字符集合,下标 ...
- Data Mining的十种分析方法——摘自《市场研究网络版》谢邦昌教授
Data Mining的十种分析方法: 记忆基础推理法(Memory-Based Reasoning:MBR) 记忆基础推理法最主要的概念是用已知的案例(case)来预测未来案例的一些属 ...
- 头像截取 图片上传 js插件
先看一下整体效果 页面html <div class="row"> <div class="tabs-container"> <u ...
