【BZOJ2693】jzptab [莫比乌斯反演]

jzptab

Time Limit: 10 Sec  Memory Limit: 512 MB
[Submit][Status][Discuss]

Description

 　　求

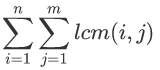
Input

　　第一行一个 T 表示数据组数

　　接下来T行 每行两个正整数 表示N、M

Output

　　T行 每行一个整数 表示第i组数据的结果

Sample Input

　　1
　　4 5

Sample Output

　　122

HINT

　　T <= 10000
　　N, M<=10000000

Solution

　　我们先根据BZOJ2154运用莫比乌斯反演推到一个式子，然后优化求解：

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const int MOD = ;

 int T;
 int n,m;
 bool isp[ONE];
 int prime[],p_num;
 int f[ONE];
 s64 Ans,sum[ONE];

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Getf(int MaxN)
 {
         f[] = ;
         for(int i=; i<=MaxN; i++)
         {
             if(!isp[i])
                 prime[++p_num] = i, f[i] = (-(s64)i*i%MOD+i+MOD)%MOD;
             for(int j=; j<=p_num, i*prime[j]<=MaxN; j++)
             {
                 isp[i * prime[j]] = ;
                 if(i % prime[j] == )
                 {
                     f[i * prime[j]] = (s64)f[i] * prime[j] % MOD;
                     break;
                 }
                 f[i * prime[j]] = (s64)f[i] * f[prime[j]] % MOD;
             }
         }
         for(int i=; i<=MaxN; i++)
             sum[i] = (sum[i-] + f[i]) % MOD;
 }

 s64 Sum(int n,int m)
 {
         return ((s64)n*(n+)/%MOD) * ((s64)m*(m+)/%MOD) % MOD;
 }

 void Solve()
 {
         n=get();    m=get();
         if(n > m) swap(n,m);
         Ans = ;
         for(int i=, j=; i<=n; i=j+)
         {
             j = min(n/(n/i), m/(m/i));
             Ans += Sum(n/i,m/i) * ((s64)sum[j] - sum[i-] + MOD) % MOD;
             Ans %= MOD;
         }
         printf("%lld\n",Ans);
 }

 int main()
 {
         Getf(ONE-);
         T=get();
         while(T--)
             Solve();
 }