CAS 逻辑流程图
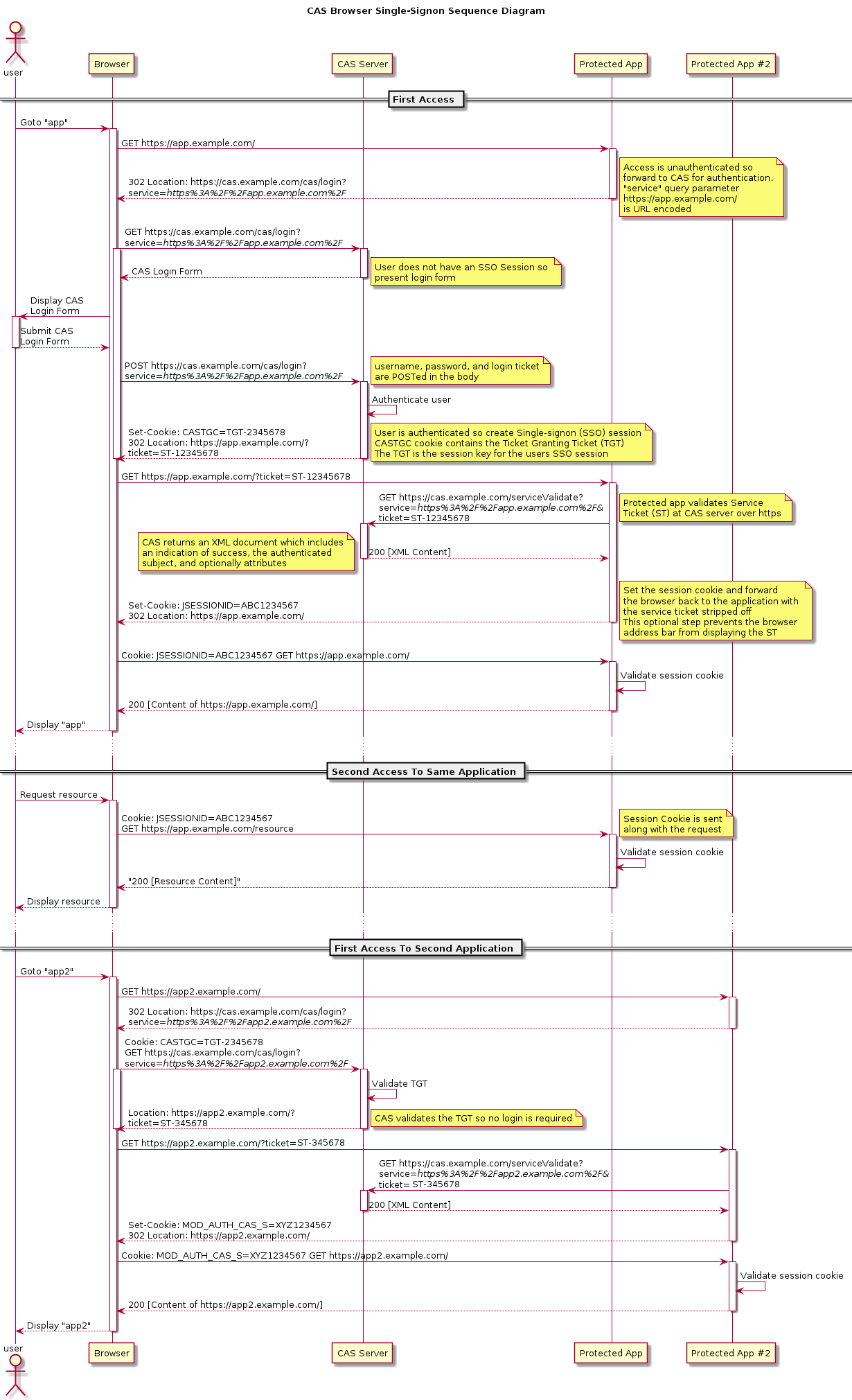
CAS 逻辑流程图的更多相关文章
- [转]单点登录SSO学习——CAS协议内容
作者:anmaler 本文转自:http://blog.zhaojunling.me/p/24 CAS中文文档甚少,这篇文章对CAS接口参数有比较清楚的说明,排版也不错查阅舒适 在当前互联网产品中使用 ...
- .NET应用和AEAI CAS集成详解
1 概述 数通畅联某综合SOA集成项目的统一身份认证工作,需要第三方系统配合进行单点登录的配置改造,在项目中有需要进行单点登录配置的.NET应用系统,本文专门记录.NET应用和AEAI CAS的集成过 ...
- SuperMap-iServer-单点登录功能验证(CAS)
SuperMap-iServer-单点登录功能验证(CAS) 1.测试目的: 验证SuperMap-iServer使用CAS单点登录的功能是否正常. 2.测试环境: SuperMap-iServer8 ...
- 集成基于CAS协议的单点登陆
相信大家对单点登陆(SSO,Single Sign On)这个名词并不感到陌生吧?简单地说,单点登陆允许多个应用使用同一个登陆服务.一旦一个用户登陆了一个支持单点登陆的应用,那么在进入其它使用同一单点 ...
- 【Java并发编程实战】-----“J.U.C”:CAS操作
CAS,即Compare and Swap,中文翻译为"比较并交换". 对于JUC包中,CAS理论是实现整个java并发包的基石.从整体来看,concurrent包的实现示意图如下 ...
- 多线程同步工具——CAS原子变量
这是我参考的一篇文章<基于CAS的乐观锁实现>,讲述的是一种需要CPU支持的执行技术CAS(Compare and Swap). 首先理解什么是原子性操作,意思是不能再拆分的操作,例如改写 ...
- CAS FOR WINDOW ACTIVE DIRECTORY SSO单点登录
一.CAS是什么? CAS(Central Authentication Service)是 Yale 大学发起的一个企业级的.开源的项目,旨在为 Web 应用系统提供一种可靠的单点登录解决方法(支持 ...
- CAS Client集群环境的Session问题及解决方案
[原创申明:文章为原创,欢迎非盈利性转载,但转载必须注明来源] 之前写过一篇文章,介绍单点登录的基本原理.这篇文章重点介绍开源单点登录系统CAS的登录和注销的实现方法.并结合实际工作中碰到的问题,探讨 ...
- cas单点登录搭建
Cas Server下载:http://developer.jasig.org/cas/ Cas Client下载:http://developer.jasig.org/cas-clients/ 测试 ...
随机推荐
- 定点数(fixed-point number)
定义 定点数(fixed-point number)就是小数点位置固定的数,也就是说,小数点后面的位数是固定的,比如要记录一笔账目,这些账目的数字都不会超过100,就可以使用2位小数位定点数来记录,比 ...
- StrBlob类——智能指针作为成员
/* 管理string的类 使用vector来管理元素 由于类对象被销毁时相应的元素成员也将销毁 所以需要将vector保存在动态内存中 */ //该程序鲁棒性不强,没有考虑到vector为空的情况 ...
- 你代码写得这么丑,一定是因为你长得不好看----panboo第一篇博客
一.个人介绍 我叫潘博,软嵌162,学号1613072055. 以“panboo”名称混迹于各大开源IT论坛与博客. 除了编程,我的最大爱好是篮球与健身,热衷于各种IT技术与运动. 我做过的软件项目有 ...
- 2019寒假训练营寒假作业(二) MOOC的网络空间安全概论笔记部分
视频课程--MOOC的网络空间安全概论笔记 第一章 网络空间安全概述 2001年,网络空间概念被首次提出: 网络空间安全框架: 1.设备层安全: 可通过截获电磁辐射获取计算机信息.通过硬件木马(恶意电 ...
- 3dContactPointAnnotationTool开发日志(十四)
貌似每次让用户手动输入文件路径太不人道了,于是参考Unity 实用教程 之 调用系统窗口选择文件或路径增加了让用户浏览文件的功能,点击输入框旁边的+就可以找到文件并加载进来: 貌似调整位置再计 ...
- node中的__dirname
先说结论:__dirname指的是当前文件所在文件夹的绝对路径. 测试路径如下: 即 根目录/dir0.js 根目录/path1/dir1.js 根目录/paht1/path2/dir2.js 每个d ...
- server2003 必要的系统优化和安全设置
修改远程桌面端口: Windows 2003系统中的远程终端服务是一项功能非常强大的服务,同时也成了入侵者长驻主机的通道,入侵者可以利用一些手段得到管理员账号和密码并入侵主机.下面,我们来看看如何通过 ...
- cacti 添加mysql 监控 (远程服务器)
监控主机 192.168.24.69 ,以下用A表示 被监控主机 192.168.24.79,以下用B标识 记得在A服务器的cacti中导入监控mysql的templates文件 1.在B上安 ...
- JQuery 学习笔记--02
JS 中的 window.onload() 方法与 Jquery 中的 $(document).read(function( ){ }) 的区别 : 加载时机不一样, window.onload() ...
- ADO.NET中DataSet、DataTable、DataRow的数据复制方法
DataSet 对象是支持 ADO.NET的断开式.分布式数据方案的核心对象 ,用途非常广泛.我们很多时候需要使用其中的数据,比如取得一个DataTable的数据或者复制另一个DataTabe中的数据 ...
