BZOJ4827：[AH2017/HNOI2017]礼物——题解

https://www.lydsy.com/JudgeOnline/problem.php?id=4827

https://www.luogu.org/problemnew/show/P3723

题面见原题。

参考了洛谷一些题解。

先推式子，x数组为a，y数组为b，将b数组倍长后有：

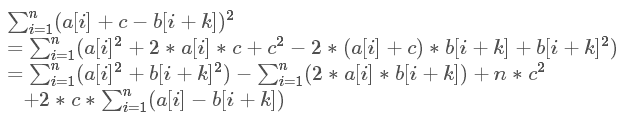
因为c的范围在[-m,m]之间，而m=100，且稍加思考后发现k在1,3,4项中是无用的，所以通过枚举c取得1,3,4项和的最小值。

考虑计算第二项，其实是卷积型，实际上将a数组前移并倒转即可得到：

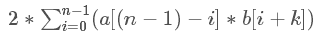
变成了卷积，FFT即可O(nlogn)，本题结束。

（PS：防止我以后看不懂写点东西）

（从n-1枚举到FFT的长度，在之间取得最大值即可）

（至于为什么k可以被忽略，是因为当长度大于n-1时b[k]之前的项相当于乘了个0所以没事。）

（当然我写的时候发现答案对了就交了结果就阴差阳错的AC了:) ）

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cctype>
#include<cstdio>
#include<queue>
#include<cmath>
using namespace std;
typedef long double dl;
typedef long long ll;
const dl pi=acos(-1.0);
const int N=2e6+;
inline int read(){
    int X=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<)+(X<<)+(ch^),ch=getchar();
    return w?-X:X;
}
struct complex{//定义复数
    dl x,y;
    complex(dl xx=0.0,dl yy=0.0){
        x=xx;y=yy;
    }
    complex operator +(const complex &b)const{
        return complex(x+b.x,y+b.y);
    }
    complex operator -(const complex &b)const{
        return complex(x-b.x,y-b.y);
    }
    complex operator *(const complex &b)const{
        return complex(x*b.x-y*b.y,x*b.y+y*b.x);
    }
};
void FFT(complex a[],int n,int on){
    for(int i=,j=n>>;i<n-;i++){
        if(i<j)swap(a[i],a[j]);
        int k=n>>;
        while(j>=k){j-=k;k>>=;}
        if(j<k)j+=k;
    }
    for(int i=;i<=n;i<<=){
        complex res(cos(-on**pi/i),sin(-on**pi/i));
        for(int j=;j<n;j+=i){
            complex w(,);
            for(int k=j;k<j+i/;k++){
                complex u=a[k],t=w*a[k+i/];
                a[k]=u+t;
                a[k+i/]=u-t;
                w=w*res;
            }
        }
    }
    if(on==-)
        for(int i=;i<n;i++)a[i].x/=n;
}
complex a[N],b[N];
int n,m;
ll t1=,t2=,t3=,t4=;
inline ll suan(int c){
    return (ll)n*c*c+*(t3-t4)*c;
}
int main(){
    n=read(),m=read();
    for(int i=n-;i>=;i--)a[i].x=read();
    for(int i=;i<n;i++)b[i].x=read();
    for(int i=;i<n;i++){
        t1+=a[i].x*a[i].x;t2+=b[i].x*b[i].x;
        t3+=a[i].x;t4+=b[i].x;
    }

    for(int i=n;i<*n;i++)b[i]=b[i-n];
    int k=;while(k<n*)k<<=;
    FFT(a,k,);FFT(b,k,);
    for(int i=;i<k;i++)a[i]=a[i]*b[i];
    FFT(a,k,-);

    ll maxn=,minn=1e18;
    for(int i=n-;i<k;i++)maxn=max(maxn,(ll)(a[i].x+0.5));
    for(int i=-m;i<=m;i++)
        if(suan(i)<minn)minn=suan(i);
    printf("%lld\n",t1+t2-*maxn+minn);
    return ;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/ +

+++++++++++++++++++++++++++++++++++++++++++