牛客网多校训练第一场 F - Sum of Maximum（容斥原理 + 拉格朗日插值法）

链接：

https://www.nowcoder.com/acm/contest/139/F

题意：

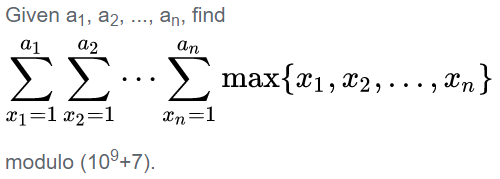
分析：

转载自：http://tokitsukaze.live/2018/07/19/2018niuke1.F/

代码：

 #include <cstdio>
 #include <cassert>
 #include <algorithm>
 using namespace std;
 
 /// 注意mod，使用前须调用一次 polysum::init(int M);
 namespace polysum {
     #define rep(i,a,n) for (int i=a;i<n;i++)
     #define per(i,a,n) for (int i=n-1;i>=a;i--)
     typedef long long ll;
     const ll mod=1e9+; /// 取模值
     ll powmod(ll a,ll b) {ll res=;a%=mod; assert(b>=); for(;b;b>>=){if(b&)res=res*a%mod;a=a*a%mod;}return res;}
 
     const int D=; /// 最高次限制
     ll a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][],C[D];
     ll calcn(int d,ll *a,ll n) {
         if (n<=d) return a[n];
         p1[]=p2[]=;
         rep(i,,d+) {
             ll t=(n-i+mod)%mod;
             p1[i+]=p1[i]*t%mod;
         }
         rep(i,,d+) {
             ll t=(n-d+i+mod)%mod;
             p2[i+]=p2[i]*t%mod;
         }
         ll ans=;
         rep(i,,d+) {
             ll t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
             if ((d-i)&) ans=(ans-t+mod)%mod;
             else ans=(ans+t)%mod;
         }
         return ans;
     }
     void init(int M) { /// M：最高次
         f[]=f[]=g[]=g[]=;
         rep(i,,M+) f[i]=f[i-]*i%mod;
         g[M+]=powmod(f[M+],mod-);
         per(i,,M+) g[i]=g[i+]*(i+)%mod;
     }
     ll polysum(ll n,ll *arr,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
         for(int i = ; i <= m; i++) a[i] = arr[i];
         a[m+]=calcn(m,a,m+);
         rep(i,,m+) a[i]=(a[i-]+a[i])%mod;
         return calcn(m+,a,n-);
     }
     ll qpolysum(ll R,ll n,ll *a,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
         if (R==) return polysum(n,a,m);
         a[m+]=calcn(m,a,m+);
         ll r=powmod(R,mod-),p3=,p4=,c,ans;
         h[][]=;h[][]=;
         rep(i,,m+) {
             h[i][]=(h[i-][]+a[i-])*r%mod;
             h[i][]=h[i-][]*r%mod;
         }
         rep(i,,m+) {
             ll t=g[i]*g[m+-i]%mod;
             if (i&) p3=((p3-h[i][]*t)%mod+mod)%mod,p4=((p4-h[i][]*t)%mod+mod)%mod;
             else p3=(p3+h[i][]*t)%mod,p4=(p4+h[i][]*t)%mod;
         }
         c=powmod(p4,mod-)*(mod-p3)%mod;
         rep(i,,m+) h[i][]=(h[i][]+h[i][]*c)%mod;
         rep(i,,m+) C[i]=h[i][];
         ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
         if (ans<) ans+=mod;
         return ans;
     }
 }
 
 typedef long long int LLI;
 const LLI MOD = polysum::mod;
 const int UP = 1e3 + ;
 LLI a[UP], b[UP];
 
 int main() {
     polysum::init(UP);
     int n;
     while(~scanf("%d", &n)) {
         for(int i = ; i <= n; i++) scanf("%lld", &a[i]);
         sort(a+, a+n+);
         LLI ans = , prod = ;
         for(int i = ; i <= n; i++) {
             if(a[i] == a[i-]) {
                 prod = prod * a[i] % MOD;
                 continue;
             }
             for(int x = ; x <= n-i+; x++) {
                 b[x] = (polysum::powmod(x, n-i+) - polysum::powmod(x-, n-i+) + MOD) % MOD * x % MOD;
             }
             LLI temp = (polysum::polysum(a[i]+, b, n-i+) - polysum::polysum(a[i-]+, b, n-i+) + MOD) % MOD;
             ans = (ans + prod * temp % MOD) % MOD;
             prod = prod * a[i] % MOD;
         }
         printf("%lld\n", ans);
     }
     return ;
 }

拉格朗日插值法模板（杜教版）：

 /// 注意mod，使用前须调用一次 polysum::init(int M);
 namespace polysum {
     #define rep(i,a,n) for (int i=a;i<n;i++)
     #define per(i,a,n) for (int i=n-1;i>=a;i--)
     typedef long long ll;
     const ll mod=1e9+; /// 取模值
     ll powmod(ll a,ll b) {ll res=;a%=mod; assert(b>=); for(;b;b>>=){if(b&)res=res*a%mod;a=a*a%mod;}return res;}
 
     const int D=; /// 最高次限制
     ll a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][],C[D];
     ll calcn(int d,ll *a,ll n) {
         if (n<=d) return a[n];
         p1[]=p2[]=;
         rep(i,,d+) {
             ll t=(n-i+mod)%mod;
             p1[i+]=p1[i]*t%mod;
         }
         rep(i,,d+) {
             ll t=(n-d+i+mod)%mod;
             p2[i+]=p2[i]*t%mod;
         }
         ll ans=;
         rep(i,,d+) {
             ll t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
             if ((d-i)&) ans=(ans-t+mod)%mod;
             else ans=(ans+t)%mod;
         }
         return ans;
     }
     void init(int M) { /// M：最高次
         f[]=f[]=g[]=g[]=;
         rep(i,,M+) f[i]=f[i-]*i%mod;
         g[M+]=powmod(f[M+],mod-);
         per(i,,M+) g[i]=g[i+]*(i+)%mod;
     }
     ll polysum(ll n,ll *arr,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
         for(int i = ; i <= m; i++) a[i] = arr[i];
         a[m+]=calcn(m,a,m+);
         rep(i,,m+) a[i]=(a[i-]+a[i])%mod;
         return calcn(m+,a,n-);
     }
     ll qpolysum(ll R,ll n,ll *a,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
         if (R==) return polysum(n,a,m);
         a[m+]=calcn(m,a,m+);
         ll r=powmod(R,mod-),p3=,p4=,c,ans;
         h[][]=;h[][]=;
         rep(i,,m+) {
             h[i][]=(h[i-][]+a[i-])*r%mod;
             h[i][]=h[i-][]*r%mod;
         }
         rep(i,,m+) {
             ll t=g[i]*g[m+-i]%mod;
             if (i&) p3=((p3-h[i][]*t)%mod+mod)%mod,p4=((p4-h[i][]*t)%mod+mod)%mod;
             else p3=(p3+h[i][]*t)%mod,p4=(p4+h[i][]*t)%mod;
         }
         c=powmod(p4,mod-)*(mod-p3)%mod;
         rep(i,,m+) h[i][]=(h[i][]+h[i][]*c)%mod;
         rep(i,,m+) C[i]=h[i][];
         ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
         if (ans<) ans+=mod;
         return ans;
     }
 }