hdu3483之二项式展开+矩阵快速幂

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 589    Accepted Submission(s): 305

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*10
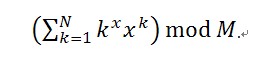
⁹, and 1 ≤ x ≤ 50.

The input ends up with three negative numbers, which should not be processed as a case.

 

Output

For each test case, print a line with an integer indicating the result.

 

Sample Input

100 1 10000
3 4 1000
-1 -1 -1

 

Sample Output

5050
444

/*分析:
Sn=1^x * x^1 + 2^x * x^2 +...+ n^x * x^n;
Sn+1=1^x * x^1 + 2^x * x^2 +...+ n^x * x^n+(n+1)^x * x^(n+1)=Sn+(n+1)^x * x^(n+1),将(n+1)^x二项式展开然后用矩阵快速幂
构造矩阵:
|1 xC(x,0) xC(x,1) xC(x,2) ... xC(x,x)|  |Sn	   | |S(n+1)		   |
|0 xC(0,0) 0       0       ... 0	  |  |x^n * n^0| |x^(n+1) * (n+1)^0|
|0 xC(1,0) xC(1,1) 0       ... 0	  | *|x^n * n^1|=|x^(n+1) * (n+1)^1|
|0 xC(2,0) xC(2,1) xC(2,2) ... 0	  |  |x^n * n^2| |x^(n+1) * (n+1)^2|
|...								  |  |...	   | |...			   |
|0 xC(x,0) xC(x,1) xC(x,2) ... xC(x,x)|  |x^n * n^x| |x^(n+1) * (n+1)^x|
*/
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;

const int MAX=50+10;
__int64 array[MAX][MAX],sum[MAX][MAX],mod;

__int64 C(int n,int m){
	if(m<0 || m>n)return 0;
	__int64 ans=1;
	for(int i=1;i<=m;++i){
		ans=ans*(n-m+i)/i;
	}
	return ans%mod;
}

void MatrixInit(__int64 a[MAX][MAX],int &x,bool flag){
	a[0][0]=1;
	for(int j=1;j<=x+1;++j){
		if(flag)a[0][j]=x*C(x,j-1)%mod;
		else a[0][j]=0;
	}
	for(int i=1;i<=x+1;++i){
		for(int j=0;j<=x+1;++j){
			if(flag)a[i][j]=x*C(i-1,j-1)%mod;
			else a[i][j]=(i == j);
		}
	}
}

void MatrixMult(__int64 a[MAX][MAX],__int64 b[MAX][MAX],int &x){
	__int64 c[MAX][MAX]={0};
	for(int i=0;i<=x+1;++i){
		for(int j=0;j<=x+1;++j){
			for(int k=0;k<=x+1;++k){
				c[i][j]=(c[i][j]+a[i][k]*b[k][j])%mod;
			}
		}
	}
	for(int i=0;i<=x+1;++i){
		for(int j=0;j<=x+1;++j)a[i][j]=c[i][j];
	}
}

__int64 MatrixPow(int &x,int &k){
	MatrixInit(sum,x,0);
	while(k){
		if(k&1)MatrixMult(sum,array,x);
		MatrixMult(array,array,x);
		k>>=1;
	}
	return sum[0][1];
}

int main(){
	int n,x;
	while(scanf("%d%d%I64d",&n,&x,&mod),n>0){
		MatrixInit(array,x,1);
		printf("%I64d\n",MatrixPow(x,n));
	}
	return 0;
}