2017 ACM ICPC Asia Regional - Daejeon

2017 ACM ICPC Asia Regional - Daejeon

Problem A Broadcast Stations

题目描述：给出一棵树，每一个点有一个辐射距离\(p_i\)（待确定），但\(p_i==0\)的点不能辐射自己，只能由别的点辐射覆盖。求\(p_i\)的和的最小值。

Problem B Connect3

题目描述：有一个\(4 \times 4\)的网格，两个人玩游戏，第一个人用黑棋，第二人用白棋。每次选择一列，将棋子扔下去，直到最下一个空的格子。现在给出第一个人下的位置，以及最后第二个人下的棋子最终的位置。已知最后一步是赢棋的一步，问最终有多少种棋盘状态。

solution
因为状态数很少，所以可以直接暴力搜索最终的状态。

时间复杂度：\(O(2^{16}*16)\)

Problem C Game Map

题目描述：给出一个\(n\)个点的图，设每个点的度为\(d_i\)，选出一个最长的序列\(c_i\)，满足\(d_{c_i}<d_{c_{i+1}}\)，且\(c_i\)与\(c_{i+1}\)相邻，输出最长的长度。

solution
将点按度排序，每个点\(i\)向度比\(d_i\)大的邻居连一条有向边，然后DAG \(dp\)。

时间复杂度：\(O(n)\)

Problem D Happy Number

题目描述：设函数\(f(n)\)，\(f(n)\)等于\(n\)的每一位的数的平方的和，将得出的结果继续带进\(f\)继续算，直到等于\(1\)，如果能等于\(1\)，则称\(n\)是开心的数，否则是不开心的数。给出一个数\(n\)，判断是否是开心的数。

solution
暴力模拟，记忆化\(n \leq 1000\)的数是否开心。

时间复杂度：\(O(1000*10)\)

Problem E How Many to Be Happy?

题目描述：给出一个有\(n\)个点\(m\)条边的图，每条边有一个边权，问要使第\(i\)条边成为图的最小生成树的一条边最少要删掉多少条边，求出每条边的对应答案的和。

solution
枚举边\(i\)，找出那些边权小于\(i\)的边权的边，这些边都是网络流里的边，然后以\(i\)的两个点为源点和汇点跑网络流求最小割。

时间复杂度：\(O(mn^2m)\)(远小于这个值)

Problem F Philosopher’s Walk

题目描述：按以下规则构建路线：其中\(W_i\)的左上角和右上角都是\(W_{i-1}\)，左下角为\(W_{i-1}\)顺时针转\(90^{\circ}\)，右下角为\(W_{i-1}\)逆时针转\(90^{\circ}\)。从\((1, 1)\)出发沿线编号。给出\(x, y\)，求出\(W_x\)中编号为\(y\)的格子坐标。

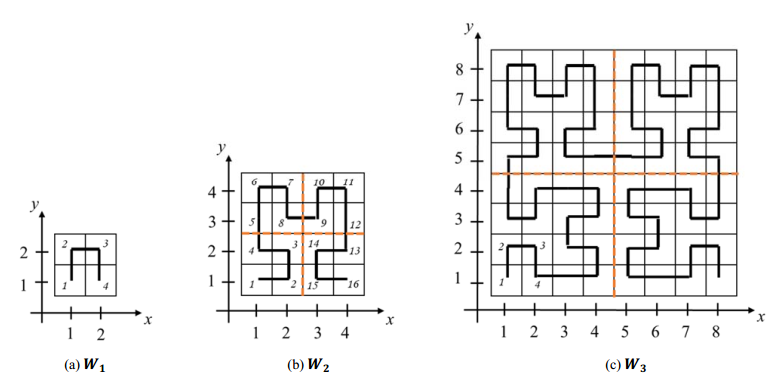
solution
分治求解，缩减图的规模，递归回来之后进行坐标变换即可。

时间复杂度：\(O(k)\)

Problem G Rectilinear Regions

题目描述：给出两条阶梯型的线\(L, U\)，求出那些\(U\)在上，\(L\)在下围成的多边形的面积的和。

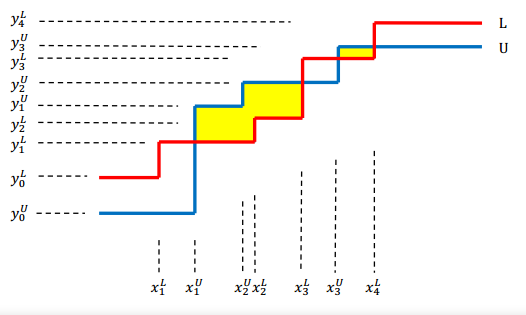
solution
观察可得，多边形的左边为\(U\)的竖线与\(L\)的横线相交，右边为\(U\)的横线与\(L\)的竖线相交。枚举\(U\)的每一级，二分出\(L\)对应的位置，判断是否相交。将相交的地方映射到\(x\)轴，若相邻的相交类型是上述的类型，就用部分和算出围成的多边形的面积。

时间复杂度：\(O(nlogn)\)

Problem H Rock Paper Scissors

题目描述：给出两个剪刀(S)石头(R)布(P)的序列，确定第一个序列的一个位置作为第二个序列的开始位置，算出第二个序列能多少局。求出第二个序列最多能赢多少局。

solution
先将第一个序列的每一位变成能赢这一位的字符。问题变成一个匹配问题。
将这个序列分成三个序列，每个序列分别只有剪刀、石头、布。同样将第二个序列分成三个序列，每个序列分别只有剪刀、石头、布。

例如：
RSPPSSSRRPPR 先变成 PRSSRRRPPSSP
RRRR
将石头序列拿出来，假设第一个序列为\(a_i\)，第二个序列为\(b_i\)。按照上述的例子：
\(a=010011100000\)
\(b=1111\)
设\(f_i\)表示以\(i\)开头的区间的匹配数目，则\(f_i=\sum_{j=0}^{j<|b|} a_{i+j}*b_j\)，若将\(a_i\)翻转，则\(f_{n-i}=\sum_{j=0}^{j<|b|} a_{n-(i+j)}*b_j\)，就是卷积。
同理算出剪刀序列和布序列，求和，求最大值。

时间复杂度：\(O(9nlogn)\)

Problem I Slot Machines

题目描述：给出一个长度为\(n\)的序列\(a_i\)，这个序列第\(k+1\)起到最后是若干个循环，周期为\(p\)，最后一个循环可以不完整。求\(k+p\)最小值对应的\(k, p\)。

solution
将序列\(a_i\)翻转，做一次\(KMP\)(\(fail[i]\))，枚举\(k+1\)的位置\(i\)，则周期\(p=i-fail[i], k=n-i\)。更新答案。

时间复杂度：\(O(n)\)

Problem K Untangling Chain

题目描述：在二维平面上，从\((0, 0)\)出发（开始时向右走），向前走一段距离（整数），然后向左转或向右转，重复若干次。给出路径，改变每一次走的距离（不能改变转向），使得路径不相交。输出一种方案。

solution
记录\(x, y\)的最大最小值，每次走的时候走到对应的边界加一即可。

时间复杂度：\(O(n)\)

Problem L Vacation Plans

题目描述：给出\(s(s \leq 3)\)个图，每个图是一个有向图(\(n\)点，\(m\)条边)，有点权，有边权。每个图有一个目的地，出发点都是\(1\)，每一时刻经过一条边，花费为边权，或者停止不动，花费为点权。现要求同时出发，同时到达目的地，问总花费的最小值。

solution
枚举时间，三个图同时\(dp\)，更新答案，卡一下时就可以了，兜圈不会兜很多遍。

时间复杂度：\(O(n^sms)\)