java动态规划问题

这里是简单的动态规划问题。其实，如果我们学过数据结构，应该就接触过动态规划问题，当时一直没有反应过来。我们求最小生成树用的是贪婪算法。而求最短路径就是动态规划。从一个点出发，到另外每个点的最短距离。在求最短路径问题中，取一点，然后与选取与这个点连接的，最小的一条边，把这个点标上，然后求与标上点的连接的点的最短路径。我们先来看这道题目吧

1.题目描述

将一个由N行数字组成的三角形，如图所以，设计一个算法，计算出三角形的由顶至底的一条路径，使该路径经过的数字总和最小。

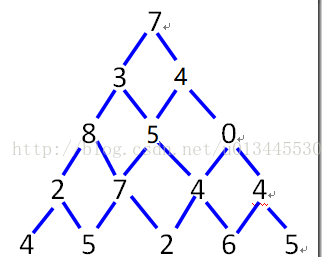
我们可以把这个横过来看变成

7

3　　4

8　　5　　0

2　　7　　4　　4

4　　5　　2　　6　　5

从顶部到底部，只能从7走到3，或者8，然后从3走到8和1，8走到1和0   。。。。

我们自己计算最小路径怎么算呢。假如从7出发，我们选择与他们两个的最长的一个，这是贪婪法，但是贪婪法有些时候不适用，比如这个图，7的话，贪婪选最小的选3，但是最短路径不是这条。

这道题目就要用到动态规划，我从底到顶部，依次求出从底部到上一层的最短路求出来。每次求最短路径，再记录下来就行。这道题目简单的地方就是上层的点到下层的路只有两条。

也就是说共有5层，用一个tem[][]来存放从底层到这个点的最短路径，那么第5层从底到自己最短路径还是本身，4,5,2,6,5。第四层的就是temp[4][j]  =  temp[4][j]  +  Min{temp[5][j],temp[5][j+1]},只有这两条路与上一层直接相连，就能直接标上。同理递归调用。。。

2.输入描述

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

3.输出描述:

输出每个点的从底部到这一点的最短路径，都记录下来。

17   
10   14   
14    7    6    
6      9    6    9    
4      5    2    6    5

4.代码示例:

package a;

import java.util.Scanner;

public class DP {
	static int qipan[][] = new int[5][5];
	static int temp[][] = new int[5][5]; //用来存放的最短路径的
	public static void main(String[] args) {
		Scanner scn = new Scanner(System.in);
		for(int i=0;i<5;i++) {
			for(int j=0;j<=i;j++) {
				qipan[i][j] = scn.nextInt();
				temp[i][j] = qipan[i][j];
			}
		}
		dp(qipan,4);//把棋盘的第5层开始求。第5层最短路是本身,数组下标是4

		//输出棋盘
		for(int i=0;i<5;i++) {
			for(int j=0;j<=i;j++) {
				System.out.printf("%-4d",temp[i][j]);
			}
			System.out.println();
		}

		//输出路径,这部分代码只是用来输出路径的，调用print路径
		temp[0][0] = -1;
		print(temp,0);
		for(int i=0;i<5;i++) {
			for(int j=0;j<=i;j++) {
				if(temp[i][j] ==-1) {
					System.out.printf("%-4d",qipan[i][j]);
				}else {
					System.out.printf("%-4d",0);
				}

			}
			System.out.println();
		}
	}
	private static void print(int[][] temp, int k) {

		if( k==4 ) {
			return;
		}
		for(int i=0;i<=k;i++) {
			if(temp[k][i]==-1) {
				if(temp[k+1][i]<temp[k+1][i+1]) {
					temp[k+1][i] = -1;
				}else {
					temp[k+1][i+1] = -1;
				}
			}
		}
		print(temp, k+1);
	}
	private static void dp(int[][] qipan, int k) {
		if(k ==0) {
			return;
		}
		for(int j=0;j<k;j++) {
			temp[k-1][j] = temp[k-1][j] + Math.min(temp[k][j], temp[k][j+1]);
		}
		dp(qipan, k-1);
	}
}