PBR Step by Step（三）BRDFs

BRDF

BRDF（Bidirectional Reflectance Distribution Function）双向反射分布函数，用来描述给定入射方向上的入射辐射度以及反射方向上的出辐射度分布，BRDF提供了一种相对准确的计算方法。

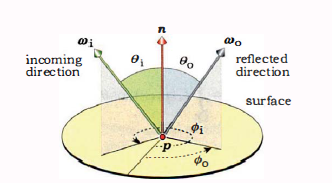
如图所示，点\({P}\)处\({d \omega}\)内的入射辐射度为\({dE_i(p, \omega_i)}\)，反射方向\({\omega_o}\)上的出射辐射度为\({dL_o(p, \omega_o)}\)。

BRDF遵循能量守恒原则，入射辐射度与出射辐射度应呈正比例关系，\({dL_o(p, \omega_o)}\)随\({dE_i(p, \omega_i)}\)的增加而增大。可表示为：

\({dL_o(p, \omega_o)} \propto {dE_i(p, \omega_i)}\)

如果用\({f_r(p, \omega_i, \omega_o)}\)表示BRDF比例系数，则：

\({dL_o(p, \omega_o)} = {f_r(p, \omega_i, \omega_o)}{dE_i(p, \omega_i)}\)

在上一篇中，我们知道入射辐射度\({dE_i(p, \omega_i)}={L_i(p, \omega_i) \, \cos \theta_i \, d \omega_i}\)，代入上式得：

\({dL_o(p, \omega_o)} = {f_r(p, \omega_i, \omega_o)}{L_i(p, \omega_i) \, \cos \theta_i \, d \omega_i}\)

那么BRDF的比例系数\({f_r(p, \omega_i, \omega_o)}=\frac{dLo(p,\omega_o)}{L_i(p,\omega_i)\, \cos \theta_i \, d\omega_i)}\)

反射辐射度方程

由上面的公式，可知在立体角\({\Omega_i}\)上的反射辐射度的方程为：

\({L_o(p,\omega_o)}=\int_{\Omega_i}{f_r(p, \omega_i, \omega_o)}\, {L_i(p, \omega_i)}\, {\cos \theta_i}\, {d\omega_i}\)

BRDFs的特征

• 满足交换率：若交换\(\omega_i\)和\(\omega_o\)，最终的BRDF值保持不变。就是说若改变光的传播方向，辐射度保持不变。
• 满足线性特征：物体表面上一点的全部反射辐射度等于各BRDF反射辐射度之和。
• 遵循能量守恒：现实中不存在可以完全反射物体表面的入射光的材质，部分能量会被物体表面吸收并以其他形式再次反射。所以物体表面面片\({dA}\)上的各向反射辐射度小于总的吸收能量。

反射率Reflatance

反射率是反射通量和入射通量的比例系数。在上一篇讲的关于辐射度的内容中，我们知道\({\Omega_i}\)上的入射辐射度：

\({E_i(p, \, \omega_i)} = \frac{d\Phi_i}{dA} = \int_{\Omega_i} {L_i(p, \, \omega_i) \, \cos \theta_i \, d \omega_i}\)

可推出\({\Omega_i}\)上的入射辐射通量\({d\Phi_i} = {dA} \int_{\Omega_i} {L_i(p, \, \omega_i) \, \cos \theta_i \, d \omega_i}\)

对于\({\Omega_o}\)上的同一面片中的反射通量为：

\({d\Phi_o} = {dA} \int_{\Omega_o}{L_o(p, \, \omega_o) \, \cos \theta_o \, d \omega_o}\)

将上面的反射辐射度方程代入，得：

\({d\Phi_o} = {dA} \int_{\Omega_o}\int_{\Omega_i} {f_r(p, \omega_i, \omega_o)}\, {L_i(p, \omega_i)}\, {\cos \theta_i}\, {d\omega_i} \, {\cos \theta_o \, d \omega_o}\)

反射率\({\rho(p, \Omega_i, \Omega_o)}=\frac{d\Phi_o}{d\Phi_i}\)，这样，我们就可以得到反射率的方程：

\({\rho(p, \Omega_i, \Omega_o)}=\frac{d\Phi_o}{d\Phi_i}=\frac{\int_{\Omega_o}\int_{\Omega_i} {f_r(p, \omega_i, \omega_o)}\, {L_i(p, \omega_i)}\, {\cos \theta_i}\, {d\omega_i} \, {\cos \theta_o \, d \omega_o}} {\int_{\Omega_i} L_i(p, \omega_i) \, \cos \theta_i \, \omega_i}\)

最后再附带上一张图作梳理总结