「LibreOJ β Round #4」求和

https://loj.ac/problem/528

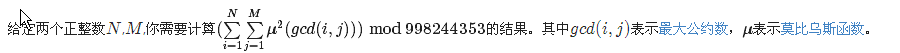
1            ，  d =1

μ（d）=   （-1）^k   ，  d=p1*p2*p3*^pk  pi为素数

0            ，  d=除以上的其他数

所以题意转化：有多少对数的gcd相同质因子只有1个

考虑容斥原理

令f（x）表示 有多少对数的gcd含有x^2这个因子

可能有一对数的gcd含有多个x^2

那么答案最终呈现 tot-f（x1）+f（x2）- f（x3）+ f（x4）……的形式

容斥系数为miu（x）

所以ans=miu（1）*f（1）+miu（2）*f（2）+miu（3）*f（3）……

f怎么算？

每隔x^2个数中一定有一个能整除x^2

所以f（x）= n/x^2  *  m/x^2

#include<cmath>
#include<cstdio>
#include<iostream>
#define N 3200001
#define mod 998244353
using namespace std;
typedef long long LL;
bool vis[N];
int p[N],miu[N],cnt;
void pre()
{
    miu[]=;
    for(int i=;i<N;i++)
    {
        if(!vis[i])
        {
            p[++cnt]=i;
            miu[i]=-;
        }
        for(int j=;j<=cnt;j++)
        {
            if(i*p[j]>=N) break;
            vis[i*p[j]]=true;
            if(i%p[j]==) break;
            miu[i*p[j]]=-miu[i];
        }
    }
}
void read(LL &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}
int main()
{
    pre();
    LL n,m;
    read(n); read(m);
    int maxn=min(sqrt(n),sqrt(m));
    int ans=;
    for(int i=;i<=maxn;i++) ans=(ans+miu[i]*(n/(1ll*i*i)%mod)*(m/(1ll*i*i)%mod)%mod+mod)%mod;
    printf("%d",ans);
}