大角度非迭代的空间坐标旋转C#实现

1. 绪论

在前面文章中提到空间直角坐标系相互转换，测绘坐标转换时，一般涉及到的情况是：两个直角坐标系的小角度转换。这个就是我们经常在测绘数据处理中，WGS-84坐标系、54北京坐标系、80西安坐标系、国家2000坐标系之间的转换。

所谓小角度转换，指直角坐标系\(XOY\)和直角坐标系\(X'O'Y'\)之间，对应轴的旋转角度很小，满足泰勒级数展开后的线性模型。

常见的三维坐标转换模型有^[1]：

• 布尔沙模型
• 莫洛琴斯基模型
• 范式模型

但，当两个坐标系对应轴的旋转角度大道一定程度时，则无法使用低阶的泰勒级数展开，且迭代的计算量、精度、速度无法取得平衡^[2]。存在以下缺点：

1. 仅适用于满足近似处理的小角度转换
2. 设计复杂的三角函数运算
3. 需要迭代计算

罗德里格矩阵是摄影测量中的常见方法，在该方法中，不需要进行三角函数的计算和迭代运算。计算过程简单明了，易于编程实现。不仅适用于小角度的坐标转换，也适用于大角度的空间坐标转换。

本文将介绍罗德里格矩阵的基本原理和C#实现，并用实例证明解算的有效性。

2. 罗德里格矩阵坐标转换原理

2.1 坐标转换基本矩阵

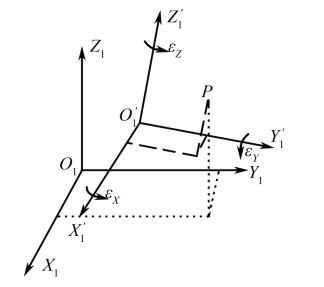
两个空间直角坐标系分别为\(XOY\)和\(X'O'Y'\)，坐标系原点不一致，存在三个平移参数\(\Delta X\)、\(\Delta Y\)、\(\Delta Z\)。它们间的坐标轴也相互不平行，存在三个旋转参数\(\epsilon x\)、\(\epsilon y\)、\(\epsilon z\)。同一点A在两个坐标系中的坐标分别为\((X,Y,Z)\)和\((X',Y',Z')\)。

显然，这两个坐标系通过坐标轴的平移和旋转变换可取得，坐标间的转换关系如下:

\[\left[\begin{array}{l}
X \\
Y \\
Z
\end{array}\right]=\lambda R\left[\begin{array}{l}
X^{\prime} \\
Y^{\prime} \\
Z^{\prime}
\end{array}\right]+\left[\begin{array}{l}
\Delta X \\
\Delta Y \\
\Delta Z
\end{array}\right] \tag{1}
\]

其中，\(\lambda\)是比例因子，\(R\left(\varepsilon_Y\right) R\left(\varepsilon_X\right) R\left(\varepsilon_Z\right)\)分别是绕Y轴，X轴，Z轴的旋转矩阵。注意，旋转的顺序不同，\(R\) 的表达形式不同。

\[\begin{aligned}
R & =R\left(\varepsilon_Y\right) R\left(\varepsilon_X\right) R\left(\varepsilon_Z\right) \\
& =\left[\begin{array}{ccc}
\cos \varepsilon_Y \cos \varepsilon_Z-\sin \varepsilon_Y \sin \varepsilon_X \sin \varepsilon_Z & -\cos \varepsilon_Y \sin \varepsilon_Z-\sin \varepsilon_Y \sin \varepsilon_X \cos \varepsilon_Z & -\sin \varepsilon_Y \cos \varepsilon_X \\
\cos \varepsilon_X \sin \varepsilon_Z & \cos \varepsilon_X \cos \varepsilon_Z & -\sin \varepsilon_X \\
\sin \varepsilon_Y \cos \varepsilon_Z+\cos \varepsilon_Y \sin \varepsilon_X \sin \varepsilon_Z & -\sin \varepsilon_Y \sin \varepsilon_Z+\cos \varepsilon_Y \sin \varepsilon_X \cos \varepsilon_Z & \cos \varepsilon_Y \cos \varepsilon_X
\end{array}\right]
\end{aligned}
\]

习惯上称\(R\)为旋转矩阵，\([\Delta X,\Delta Y,\Delta Z]^T\)为平移矩阵。只要求出\(\Delta X\)、\(\Delta Y\) 、\(\Delta Z\)，\(\varepsilon_X\)、\(\varepsilon_Y\)、\(\varepsilon_Z\)，这7个转换参数,或者直接求出旋转矩阵和平移矩阵,就可以实现两个坐标系间的转换。

2.2 计算技巧-重心矩阵

为计算方便，对所用到的坐标进行重心化处理。将两个坐标系的公共点的坐标均化算为以重心为原点的重心化坐标。分别记为\((\bar{X}, \bar{Y}, \bar{Z})\)和\(\left(\bar{X}^{\prime}, \bar{Y}^{\prime}, \bar{Z}^{\prime}\right)\)两个坐标系的重心的坐标分别为\((X_g, Y_g, Z_g)\)和\((X'_g, Y'_g, Z'_g)\)。

\[\left\{\begin{array}{l}
X_k=\frac{\sum_{i=1}^n X_i}{n}, Y_k=\frac{\sum_{i=1}^n Y_i}{n}, Z_k=\frac{\sum_{i=1}^n Z_i}{n} \\
X_k^{\prime}=\frac{\sum_{i=1}^n X_i^{\prime}}{n}, Y_k^{\prime}=\frac{\sum_{i=1}^n Y_i^{\prime}}{n}, Z_k^{\prime}=\frac{\sum_{i=1}^n Z_i^{\prime}}{n} \\
\bar{X}_i=X_i-X_k, \bar{Y}_i=Y_i-Y_k, \bar{Z}_i=Z_i-Z_k \\
\bar{X}_i^{\prime}=X_i^{\prime}-X_k^{\prime}, \bar{Y}_i^{\prime}=Y_i^{\prime}-Y_k^{\prime}, \bar{Z}_i^{\prime}=Z_i^{\prime}-Z_k^{\prime}
\end{array}\right.
\]

因此，可以将式(1)变为：

\[\left[\begin{array}{l}
\bar{X} \\
\bar{Y} \\
\bar{Z}
\end{array}\right]=\lambda R\left[\begin{array}{l}
\bar{X}^{\prime} \\
\bar{Y}^{\prime} \\
\bar{Z}^{\prime}
\end{array}\right] \tag{2}
\]

\[\left[\begin{array}{l}
\Delta X \\
\Delta Y \\
\Delta Z
\end{array}\right]=\left[\begin{array}{l}
X_g \\
Y_g \\
Z_g
\end{array}\right]-\lambda R\left[\begin{array}{l}
X_g^{\prime} \\
Y_g^{\prime} \\
Z_g^{\prime}
\end{array}\right] \tag{3}
\]

因而，转换参数可分两步来求解。先用式(2)求出旋转参数和比例因子，再用式(,3)求出平移参数。

2.3 基于罗德里格斯矩阵的转换方法

对式(2)两边取2-范数，由于\(\lambda > 0\)，旋转矩阵为正交阵的特性，可得:

\[\Vert [\bar{X}, \bar{Y}, \bar{Z}]^T \Vert = \lambda \Vert [\bar{X'}, \bar{Y'}, \bar{Z'}]^T \Vert \tag{4}
\]

对于n个公共点，可得\(\lambda\)的最小均方估计:

\[\lambda=\frac{\sum_{i=1}^n\left(\left\|\left[\bar{X}_i \bar{Y}_i \bar{Z}_i\right]^{\mathrm{T}}\right\| \cdot\left\|\left[\bar{X}_i^{\prime} \bar{Y}_i^{\prime} \bar{Z}_i^{\prime}\right]^{\mathrm{T}}\right\|\right)}{\sum_i^n\left(\left\|\left[\bar{X}_{\prime}^{\prime} \bar{Y}_i^{\prime} \bar{Z}_i^{\prime}\right]^{\mathrm{T}}\right\|\right)^2}
\]

得到比例因子的最小均方估计后，可将旋转矩阵 \(R\) 表示为:

\[R=(I-S)^{-1} (I+S) \tag{5}
\]

其中，\(I\)为单位矩阵，\(S\)为反对称矩阵。将式(5)带入式(3)，可得：

\[\left[\begin{array}{c}
\bar{X}-\lambda \bar{X}^{\prime} \\
\bar{Y}-\lambda \bar{Y}^{\prime} \\
\bar{Z}-\lambda \bar{Z}^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
0 & -\left(\bar{Z}+\lambda \bar{Z}^{\prime}\right) & -\left(\bar{Y}+\lambda \bar{Y}^{\prime}\right) \\
-\left(\bar{Z}+\lambda \bar{Z}^{\prime}\right) & 0 & \bar{X}+\lambda \bar{X}^{\prime} \\
\bar{Y}+\lambda \bar{Y}^{\prime} & \bar{X}+\lambda \bar{X}^{\prime} & 0
\end{array}\right]\left[\begin{array}{l}
a \\
b \\
c
\end{array}\right] \tag{6}
\]

3. C#代码实现

矩阵运算使用MathNet.Numerics库，初始化字段MatrixBuilder<double> mb = Matrix<double>.Build和VectorBuilder<double> vb = Vector<double>.Build

3.1 计算矩阵重心坐标

Vector<double> BarycentricCoord(Matrix<double> coordinate)
{
    Vector<double> barycentric = vb.Dense(3, 1);

    int lenCoord = coordinate.ColumnCount;

    if (lenCoord > 2)
        barycentric = coordinate.RowSums();

    barycentric /= lenCoord;

    return barycentric;
}

3.2 计算比例因子

取2-范数使用点乘函数PointwisePower(2.0)：

double ScaleFactor(Matrix<double> sourceCoord, Matrix<double> targetCoord)
{
    double k = 0;

    double s1 = 0;
    double s2 = 0;

    Vector<double> sourceColL2Norm = sourceCoord.PointwisePower(2.0).ColumnSums();

    Vector<double> targetColL2Norm = targetCoord.PointwisePower(2.0).ColumnSums();

    int lenSourceCoord = sourceCoord.ColumnCount;

    int lenTargetCoord = targetCoord.ColumnCount;

    //只有在目标矩阵和源矩阵大小一致时，才能计算
    if (lenSourceCoord == lenTargetCoord)
    {
        s1 = sourceColL2Norm.PointwiseSqrt().PointwiseMultiply(targetColL2Norm.PointwiseSqrt()).Sum();

        s2 = sourceColL2Norm.Sum();
    }

    k = s1 / s2;
    return k;
}

3.3 计算罗德里格参数

这里的罗德里格参数就是式(6)中的\([a, b, c]^T\)。

Vector<double> RoderickParas(double scalceFactor, Matrix<double> sourceCoord, Matrix<double> targetCoord)
{
    Vector<double> roderick = vb.Dense(new double[] { 0, 0, 0 });

    int lenData = sourceCoord.ColumnCount;

    //常系数矩阵
    var lConstant = vb.Dense(new double[3 * lenData]);

    //系数矩阵
    var coefficient = mb.DenseOfArray(new double[3 * lenData, 3]);

    //构造相应矩阵
    for (int i = 0; i < lenData; i++)
    {
        lConstant[3 * i] = targetCoord[0, i] - scalceFactor * sourceCoord[0, i];
        lConstant[3 * i + 1] = targetCoord[1, i] - scalceFactor * sourceCoord[1, i];
        lConstant[3 * i + 2] = targetCoord[2, i] - scalceFactor * sourceCoord[2, i];

        coefficient[3 * i, 0] = 0;
        coefficient[3 * i, 1] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]);
        coefficient[3 * i, 2] = -(targetCoord[1, i] + scalceFactor * sourceCoord[1, i]);
        coefficient[3 * i + 1, 0] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]);
        coefficient[3 * i + 1, 1] = 0;
        coefficient[3 * i + 1, 2] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i];
        coefficient[3 * i + 2, 0] = targetCoord[1, i] + scalceFactor * sourceCoord[1, i];
        coefficient[3 * i + 2, 1] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i];
        coefficient[3 * i + 2, 2] = 0;

    }

    roderick = coefficient.TransposeThisAndMultiply(coefficient).Inverse() * coefficient.Transpose() * lConstant;

    return roderick;
}

3.4 解析罗德里格矩阵

此处，就是式(5)的实现。

/// <summary>
/// 解析罗德里格矩阵为旋转矩阵和平移矩阵
/// </summary>
/// <param name="scaleFactor">比例因子</param>
/// <param name="roderick">罗德里格矩阵</param>
/// <param name="coreSourceCoord">原坐标系坐标</param>
/// <param name="coreTargetCoord">目标坐标系坐标</param>
/// <returns></returns>
(Matrix<double>, Vector<double>) RotationMatrix(double scaleFactor, Vector<double> roderick, Vector<double> coreSourceCoord, Vector<double> coreTargetCoord)
{
    Matrix<double> rotation = mb.DenseOfArray(new double[,]
    {
        {0,0,0 },
        {0,0,0 },
        {0,0,0 }
    });

    //反对称矩阵
    Matrix<double> antisymmetric = mb.DenseOfArray(new double[,]
    {
        {          0, -roderick[2], -roderick[1] },
        {roderick[2],            0, -roderick[0] },
        {roderick[1],  roderick[0],            0 }
    });

    // 创建单位矩阵
    // 然后与式(5)的 S 执行 + 和 - 操作
    rotation = (DenseMatrix.CreateIdentity(3) - antisymmetric).Inverse() * (DenseMatrix.CreateIdentity(3) + antisymmetric);

    translation = coreTargetCoord - scaleFactor * rotation * coreSourceCoord;

    return (rotation, translation);
}

3.5 调用逻辑

// 1. 字段值准备
MatrixBuilder<double> mb = Matrix<double>.Build;
VectorBuilder<double> vb = Vector<double>.Build;

// 2. 写入源坐标系的坐标。注意这里的x,y,z输入顺序
Matrix<double> source = mb.DenseOfArray(new double[,]
{
    {-17.968, -12.829, 11.058 },
    {-0.019 , 7.117,   11.001 },
    {0.019  , -7.117,  10.981 }
}).Transpose();

// 3. 写入目标坐标系的坐标
Matrix<double> target = mb.DenseOfArray(new double[,]
{
    { 3392088.646,504140.985,17.958 },
    { 3392089.517,504167.820,17.775 },
    { 3392098.729,504156.945,17.751 }
}).Transpose();

// 4. 重心化
var coreSource = BarycentricCoord(source);
var coreTarget = BarycentricCoord(target);

var sourceCoords = source - mb.DenseOfColumnVectors(coreSource, coreSource, coreSource);
var targetCoords = target - mb.DenseOfColumnVectors(coreTarget, coreTarget, coreTarget);

// 5. 求比例因子
double k = ScaleFactor(sourceCoords, targetCoords);

// 6. 解算咯德里格参数
var roderick = RoderickParas(k, sourceCoords, targetCoords);

// 7. 旋转
(Matrix<double> ro, Vector<double> tran) = RotationMatrix(k, roderick, coreSource, coreTarget);

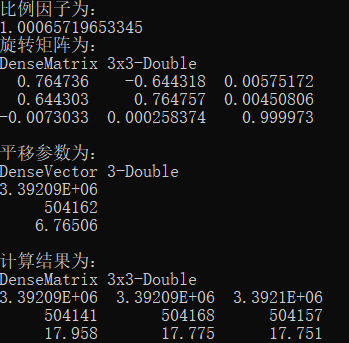
Console.WriteLine("比例因子为：");
Console.WriteLine(k);

Console.WriteLine("旋转矩阵为：");
Console.WriteLine(ro.ToString());

Console.WriteLine("平移参数为：");
Console.WriteLine(tran.ToString());

Console.WriteLine("计算结果为：");
Console.WriteLine(source2.ToString());

4. 总结

基于罗德里格矩阵的转换方法，在求解两个坐标系间的转换参数，特别是旋转角较大时，实现简单、快速。

---

1. 朱华统,杨元喜,吕志平.GPS坐标系统的变换[M].北京:测绘出版社,1994. ︎

2. 詹银虎,郑勇,骆亚波,等.无需初值及迭代的天文导航新算法0﹒测绘科学技术学报，2015,32(5):445-449. ︎