SDM

SDM:sigma delta Modulator

SC:switch capacitor(开关电容)

sigma delta调制器的分类

•单环路和级联(cascade)SDM：在于使用的量化器的数量。

仅使用一个量化器的SDM被称为单环路拓扑，而那些使用多个量化器的通常被称为级联或MASH-SDM。

•单比特与多比特量化器：区别在于嵌入的量化器的比特数。

•低通与带通：区别在于被转换信号的性质。

•离散时间DT与连续时间DT：区别在于（环路滤波器的性质）

1.1量化

量化过程还引入了对理想ADC性能的限制，因为在输入信号振幅上的连续到离散变换（通常称为量化误差）时会产生误差。量化器的操作如图1.1所示。例如，图1.1c描绘了N＝2的量化器的I/O特性，它也适用于一般的N位量化器。满标度输入范围内的输入振幅[-/2，+/2]四舍五入为1到个不同输出电平中，这些输出电平通常被编码为二进制数字表示。如果这些电平的间隔相等，则称量化器是均匀的，并且相邻输出电平之间的间隔被定义为量化步长:

(1.1)

其中表示满标度输出范围。由于和不一定相等，量化器可能表现出不同于unity(单位1)的增益，如图1.1c所示的斜率。如图1.1e所示，量化器操作因此固有地产生舍入误差，该舍入误差是输入的非线性函数。注意，如果q(n)是保持在范围[-/2，+/2]内，量化误差e(n)限定在[-/2，+/2]内。前一个输入范围被称为量化器的非过载区域，而不是e(n)的幅度单调增长的|q(n)|>/2的范围。N-bit

图1.1量化过程说明

(a)多比特量化器块，(b)单比特量化器块，y

(c)多比特量化器的I/O特性，(d)单比特量化器的I/O特性，

(e)多比特量化误差，(f)单比特量化误差

具有Q级输出电平的ADC或量化器被称为具有N位分辨率，N=。如上图所示，对于具有Q量化电平的ADC，只有被至少隔开的输入值才能被区分为不同的输出电平。需要N个数字位来编码与每个输出电平对应的Q码字。两个相邻输出电平的二进制数字码之间的差异是整个N位码字的一个最低有效位（LSB）。对于上图a，b，四电平（2bit）“midriser”和五电平（大约2bit）“midtread”ADC。与midtread ADC不同，midriser ADC不包含零输入值的零输出电平，产生了在某些应用中可能不需要的直流偏移。上图中所示的所有传输特性都是对称的。midriser需要偶数个输出电平才能生成完全对称的传输曲线，而midtread需要奇数个输出电平。对于特殊情况下的2级量化器，midtread将不能同时表示正和负输出电平，因此将严重扭曲包含两个极性的样本的信号。对于这种2级情况，几乎总是使用图2c所示的midriser特性。

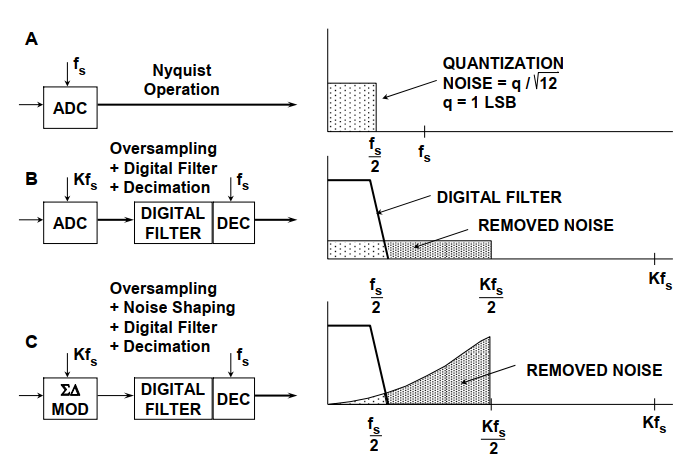
对于一个理想N位奈奎斯特率转换器，

满标度(FS)输入正弦波=v(t)=

满标度(FS)输入的rms值(功率开根号)=

所以N位奈奎斯特率转换器的RMS信噪比为SNR=20

=20=20+20 (1)

SNR=6.02N+1.76dB，dc到fs/2带宽之间

当采样频率远大于 2倍的信号频率，即采用过采样的过采样信号转换器时，由于量化噪声独立于采样频率, 所以采用过采样的量化噪声与采用奈奎斯特频率采样的量化噪声功率相同仍为 ，但他却被分布到了一个更宽的带宽内。用于转换的输入信号通带为 0~fa，数据转换器的过采样率为 OSR=，通带内的噪声能量 为：

==

=

所以对于动态精度要求为 N 位的转换器，即满幅输入为

FS= q,其理论上所能实现的信噪比为:

=

(2)

过采样来提高分辨率，由式知我们必须过采样倍才能获得N位的分辨率提高。而sigma-delta转换器不仅限制了信号的通带，而且还形成了量化噪声整形，因此不需要如此高的过采样率，如下图所示。

1.2sigma-deltaADC的噪声整形

噪声整形的概念最好在频域中通过考虑图1.2中的简单sigmadelta调制器模型来解释。

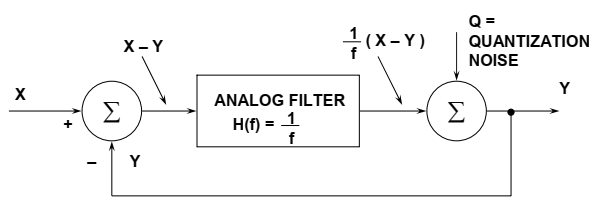
图1.2:Sigma-Delta调制器的简化频域线性化模型

Y= (3)

Y= (23)

信号项 ：噪声项

调制器中的积分器表示为具有等于H(f)=1/f的传递函数的模拟低通滤波器。该传递函数具有与输入频率成反比的振幅响应。1位量化器产生量化噪声Q，该量化噪声Q被注入到输出求和块中。如果我们让输入信号为X，输出信号为Y，则从输入求和出来的信号必须为X–Y。这将乘以滤波器传递函数1/f，结果将转到输出求和的一个输入。通过检查，我们可以将输出电压Y的表达式写成：Y=，

注意，当频率f接近零时，输出电压Y接近X，而无噪声分量。在较高的频率下，信号分量的幅度接近于零，噪声分量接近于Q。在较高的频率下，输出主要由量化噪声组成。实质上，模拟滤波器对信号具有低通效应，而对量化噪声具有高通效应。因此，模拟滤波器在∑-Δ调制器模型中执行噪声整形功能。

1.2一阶sigma-delta调制器A/D系统

一阶sigma-delta模型的框图系统如上图所示。该系统由模拟sigma-delta调制器和数字抽取器组成。调制器由一个积分器、一个内部A/D转换器或量化器和一个用于反馈路径的D/A转换器（DAC）组成。

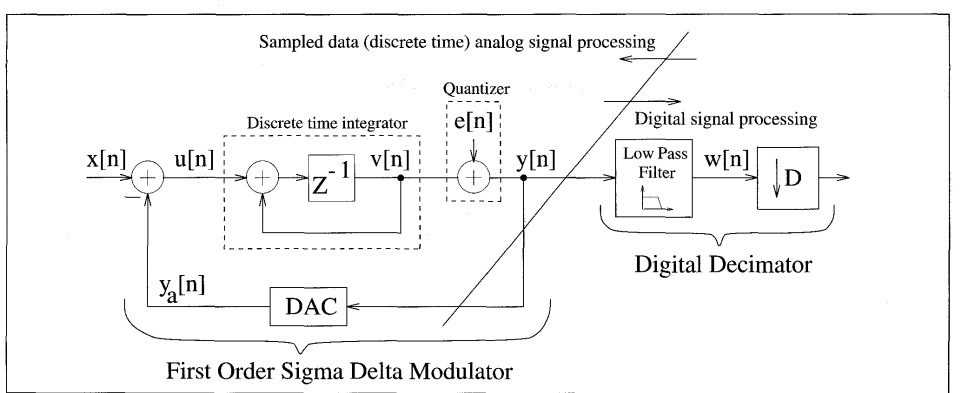
图1.3一阶sigma-delta调制器A/D系统

被量化的信号不是输入x[n]，而是输入和量化输出y[n]的模拟表示之间的差的滤波。

滤波器，通常称为前馈环路滤波器，是一个离散时间积分器，其传递函数为。

积分器和其他sigma-delta模拟电路通常采用采样数据开关电容技术实现。线性化模型用噪声源e[n]代替量化器，如上图1.3所示。

如果DAC是理想的，它将被单位增益传输函数所代替。调制器输出由     (1.2)表示。

Y(z)=

STF(z)为，NTF(z)为，

|NTF(z)|=||=||=||=|2sin()|，

在(0,fs/2)之间均匀分布的白噪声功率为，噪声的功率谱密度为，整形后信号带宽内的噪声功率为df，此时根据式（20）得到：

=

=++=3.41+6.02N+

可知当 OSR 提高一倍，信噪比提高 9dB，即增加 1.5bit 的 ADC有效分辨率。 -

考虑使用1位A/D转换器或比较器的情况，输出电平为V和-V的1bit ADC的传输特性即(1bit 量化器)。

假设V=1，1bit DAC参考电压V和-V为1和-1.比较器的数字输出y(n)为1或者-1，这样y[n]和[n]可以互换使用。在时间域中，

v(n)=u(n-1)+v(n-1), (1.3)

y(n)= (1.4)

u(n)=x(n)-y(n). (1.5)

调制器输出和输入之间的“误差”是u[n]。注意，这不是量化误差，量化误差由e[n]=y[n]-v[n]给出。因为y[n]只能为1或者-1的值，所以它永远不能等于输入，除非输入恰好是这两个值之一。因此，除了上述情况外，总是会有一个误差u[n]。考虑x[n]的直流输入，

当y[n]=1时，y[n]大于输入x[n]，且误差u[n]为负，因此积分器累加负值以产生v[n]。在多个时钟周期之后，将累积足够的负值以使量化器产生y[n]=-1，从而改变误差u[n]的符号为正。在某种意义上，输出和输入之间的误差已经减小了，因为正误差现在将在一段时间内平均，抵消先前的负误差。

现在y[n]=-1时，误差将为正值，并且误差的正值将再次累积，直到量化器输出改变，这次返回到y[n]=1。在一段时间内，1和-1的比例（或密度）将与直流输入值相关，输入越大，输出中出现的1越多，反之亦然，输入越小。因此，使用1位量化器的sigma-delta调制器的输出通常被称为脉冲密度调制（PDM）格式。

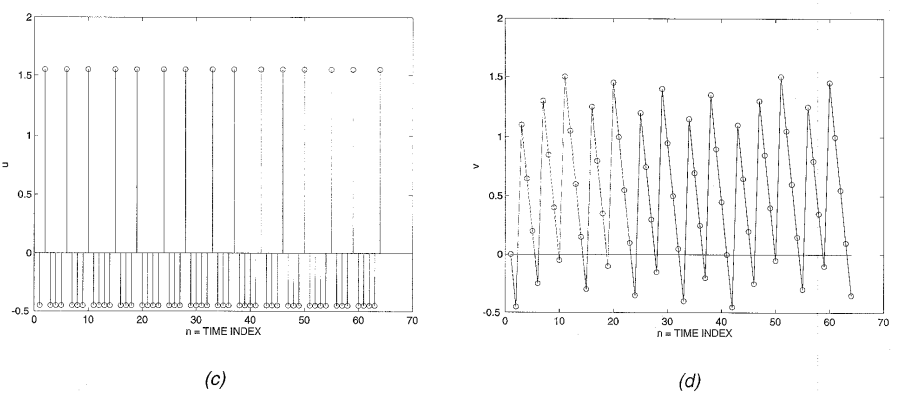
图1.4 一阶sigma delta对直流输入的响应

(a)直流输入x[n]=0.55=11/20 (b)调制器输出y[n]；

(c)”误差”信号u[n]; (d)积分器输出v[n]

下面的例子说明了时域的行为。图1.4a示出了直流输入x[n]=0.55=11/20，而图1.4b示出了相应的调制器输出y[n]，大约四分之三的输出值是1，其余的是-1。图1.4c示出了误差信号u[n]，图1.4d示出了累积误差信号或积分器输出v[n]，其符号变化迫使量化器输出为改变。对于x[n]=1的直流输入，所有调制器输出值为1。对于零直流输入，一半调制器输出值为1，一半为-1。对于-1的直流输入，所有值为-1。

通过在一段时间内平均调制器输出，我们可以逼近输入。该平均操作表示图1.3中的低通滤波块，因为平均是粗糙的低通滤波操作。对于给定的过采样率，使用更好的低通滤波器将使调制器输出更好地逼近输入。

最后，看一些正弦输入调制器输出的时域示例。图1.5a-d显示了各种正弦输入的调制器输出。对于直流输入情况，正弦幅度信息以1对-1的相对数目编码，调制器输出脉冲波形具有周期性成分，基波周期编码正弦频率。这在图1.5中尤为明显。

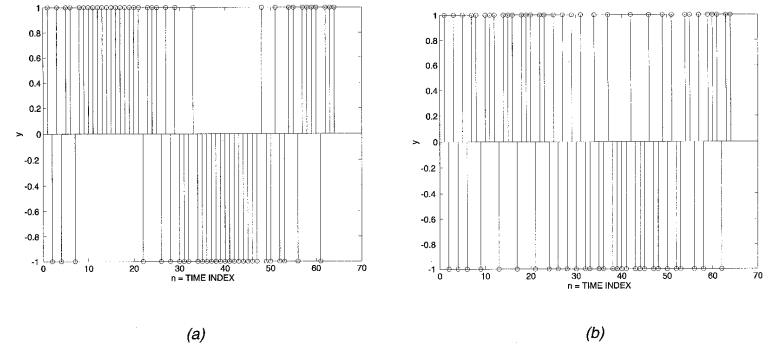
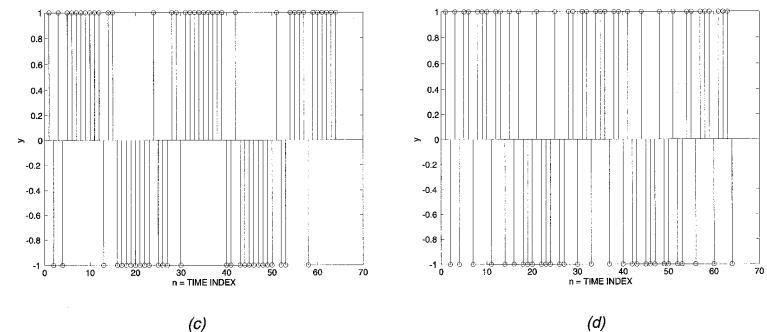
图1.5对fs约为1 MHz的各种正弦输入作出响应的一阶sigma-delta

(a)振幅=0.95，频率=20 kHz；(b)振幅=0.5，频率=20kHz；

(c)振幅=0.95，频率=40 kHz；(d)振幅=0.5，频率=40 kHz

实现缺陷

到目前为止，所给出的结果还没有考虑到模拟硬件的缺陷。现在让我们来讨论一些主电路参数存在缺陷的后果。

调制器中的积分器可以具有增益g而不是单位增益，并且可以是泄漏的。对于输入u[n]，具有增益g和泄漏因子的积分器具有输出v[n]=gu[n-1]+v[n-1]而不是v[n]=u[n-1]+v[n-1]，并且积分传递函数是而不是.

D/A增益也可能不是完全一致的，假设存在一个增益d，我们发现STF和NTF是H，STF=，NTF=。(1.6)

原来的NTF为，在z=1时有一个Z域零点（在单位圆和DC上），现在有一个零点仍然在DC，但在单位圆内移动。这会降低信号频带内的NTF噪声衰减，从而显著影响噪声性能。术语“漏”来自于在积分器电路的开关电容实现中存在电荷漏，并且只有一部分来自输入电容的电荷被转移到积分电容。

泄漏因子与用于实现开关电容积分器的运算放大器（opamp）的开环增益A相关，使得1-。

忽略存在泄露(退化)的NTF的分母（会给分子增加一点波纹），即通过将退化的NTF考虑为，我们发现具有积分器泄漏的带内量化噪声功率不再是,而退化为：

, (1.7)

现在噪声功率包含一个与过采样率成反比的项，以及与过采样率立方成反比的项。然而，第一项除以，发现如果opamp开环增益A超过过采样率，A很大，则泄漏不会导致信噪比的显著下降，因此，实现好的积分器所需的电路约束并不难满足，除非过采样率极高。

现在考虑一个不完美的DAC增益d，与单位增益不同。这可以建模为调制器输入处的1/d增益。为此，考虑在积分器的输入端插入一个1/d增益。该增益可以在图1.2中的调制器输入处移过求和节点。结果是，DAC增益d被增益1/d抵消，但现在输入在调制器之前经历了l/d的增益。因此，STF经历了轻微的增益变化，但对调制器信噪比没有太大的影响。

量化器中的缺陷

量化器中的任何非线性都可以被建模为另一个噪声源，该噪声源增加了量化误差e[n]。然而，来自该额外源的噪声受到调制器的噪声整形，因此其对信噪比衰减的影响不显著。

如果1位量化器或比较器具有非零阈值vth，则其输出由以下给出：

(1.8)

这相当于比较器输入端的偏移量，即积分器输出端的偏移量。然而，积分器的输出v[n]处的偏移对应于其输入u[n]=x[n]-y[n]处的脉冲，其等于给定x[n]的一个错误输出y[n]。一个这样的错误值将对调制器的整体性能产生可忽略的影响。偏移量也可以被建模为误差源，均值和零方差加在e[n]上。

非线性行为

sigma-delta调制器是一个包含反馈的非线性系统。调制器可能显示极限环振荡，导致在输出中存在周期（音调）分量。这种现象类似于使用有限精度算法的数字IIR滤波器中出现的极限环，因为与sigma-delta调制器一样，这种滤波器是采用反馈的非线性系统。量化器误差谱不是白噪声，因为白噪声假设的条件不完全满足，量化器只有两个输出电平，并且由于过采样，连续的量化器输入样本可能是相关的。

现在考虑调制器中极限环的存在，正如对直流输入的简单情况所做的分析，x[n]=x。对于周期T的有限环，v[n]应该也是周期性的，周期为T，即v[n]=v[n+T]。这显然意味着y[n]=y[n+T]。

对于直流输入，积分器的输入u[n]=x-y[nl，也将是周期T的周期性输入。因此，调制器的行为可以用T方程表示。

我们得到：v[n ]-v[n-1]=x[n-1]-y[n-1]，对于DC输入，它变成v[n ]-v[n-1]=x-y[n-1]。为T个不同的时间实例写下这个方程，从n=1开始（任意），把我们得到的所有方程相加，v[T ]-v[0]= -

假设v[T ]=v[0],, 其中P是T输出样本上正量化器输出的数目，M是T输出样本上负量化器输出的数目。假设T和(P-M)是整数，我们有x=，有a和b两个整数。因此，如果x是V的有理倍数，则输出y由具有周期T的有限环组成。

周期为T的有限环在输出频谱中表现为频率fs/T及其谐波的音调。如果a或b为偶数，则周期为T=2a。如果a和b都是奇数T=a。对于图1.3中x=11/20、a=20和b=11的示例可以 从图中看出，u[n]、v[n]和y[n]的预期周期确实为40。

对于x=0的特殊情况，输出在V和-V之间振荡，并且输出频谱由fs/2处的纯音组成。实际上，即使DC输入是V的无理倍数，量化噪声也不会是白色的，并且调制器输出处的频谱将是由音调组成的离散频谱。

即使对于正弦输入，量化误差也不是白色的，并且在输出中观察到强音调分量，并且音调失真分量的强度以复杂的方式取决于输入振幅。调制器输出的极低直流或正弦输入振幅的音调结构通常称为空闲信道噪声。

还有一点值得注意。可以证明，对于±V的比较器输出电平，如果调制器的输入被±V限定，则积分器的输出可以具有至多2V的幅度。从式(1.3)中很容易看出。我们还得到v[n]=x[n-1]-(y[n-1]-v[n-1])，这是因为v[n]=x[n-1]-e[n-1]。如果我们假设|v[n-1]|<2V，那么根据1位量化器的传输特性，即量化器没有过载。然后我们得到，

|v[n]|=|x[n-1]-e[n-1]|。因此，如果|x||v[n-1]|2V，那么|v[n]|2V。这可以通过确保|v[0]|2V，所以|v[1]|2V，等等来保证。

在实践中，由于一阶sigma-delta ADC的输出存在显著的音调结构，因此在诸如语音或音频等应用中很少使用，在这些应用中，即使过采样率fs/2fB足够高，能够基于线性化白噪声模型提供良好的总体信噪比，但这种音调的频率也是令人不满意的。

1.3高阶Sigma-Delta调制

提出的基本思想可以扩展到以各种方式创建sigma-delta体系结构，从而在分辨率、带宽、电路复杂性和调制器稳定性之间提供不同的权衡。我们的讨论将包括高阶、多位和多级（级联）体系结构。一般来说，为了获得性能改善，这些转换器中的大多数都需要比一阶sigma-delta调制器中使用的模拟电路更加复杂和精确。当然，所需的精度仍必须大大低于整体高转换分辨率。

1.3.1二阶SDM

对于结构图1.3.1的二阶SDM,

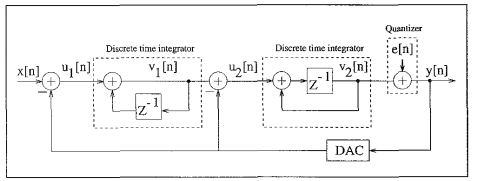
图1.3.1 二阶SDM

在时域有，

图1.3.1-1示出了二阶sigma-delta调制器的直流输入x[n]=0.55和由此产生的输出y[n]的曲线图。第一积分器的输入和输出分别为和，而第二积分器的输入和输出分别为和。调制器输入和输出之间的“误差”是，这同样不是量化误差（由e[n]=y[n]-给出）。是调制器整体“误差”的积分即（或低通滤波）再与输出y[n]之间求差。因此，可以被认为是调制器误差的更精细的版本。被量化的信号是“精细误差”的积分。因此，”和类似于一阶调制器的u[n]和v[n]。输出和是和的更精确表示，因此产生比一阶调制器的输出更精确的输出y[n]。通过比较图1.3.1-1c和图1.3.1-1e以及图1.3.1-1d和图1.3.1-1f，可以清楚地看出这一点。

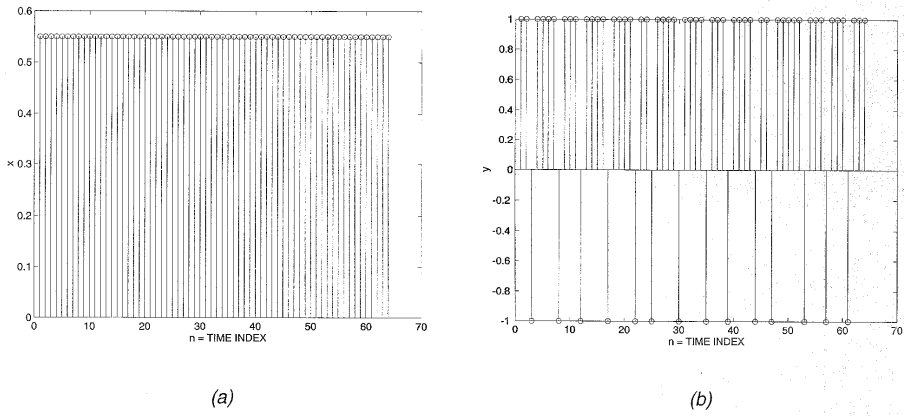
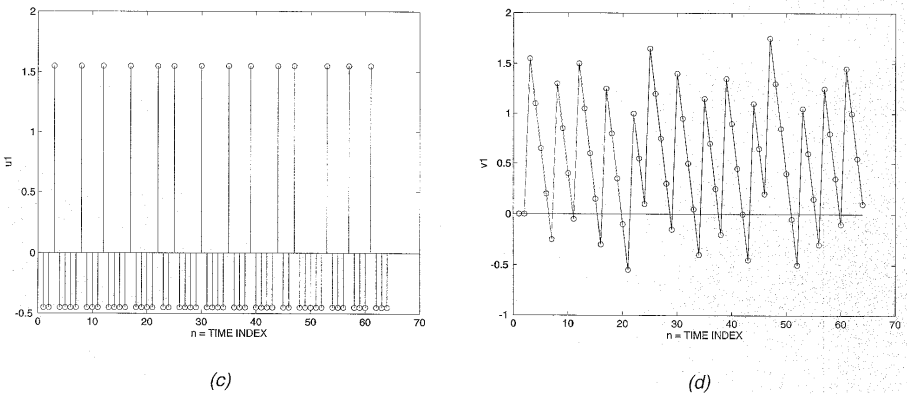
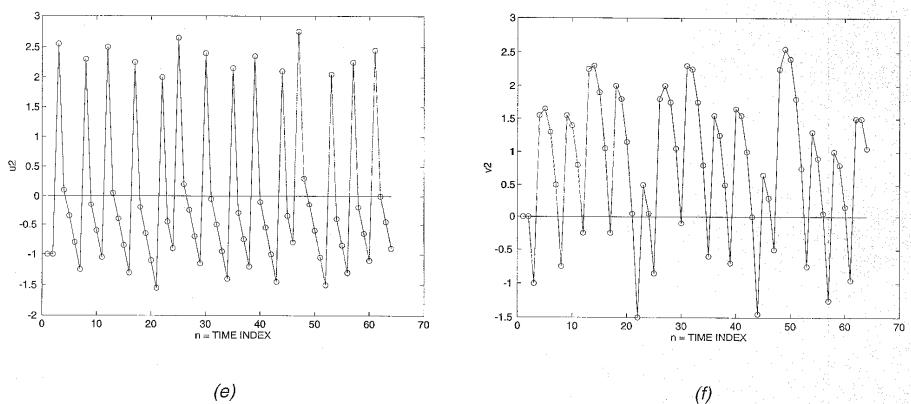
图1.3.1-1 DC输入的二阶sigma delta 响应

(a) x(n)=0.55的DC输入 (b)y(n)输出

(c)误差信号 (d)第一阶积分器输出

(e)更精细的误差信号 (f) 第二阶积分器输出

在将图1.3.1-1b的二阶sigmadelta的y[n]与图1.4中一阶sigmadelta的y[n]进行比较时，关键在于图1.3.1-1b中1和-1的分布是这样的，它们的平均值提供了比一阶调制器输出的相应平均值更精确的输入表示。换句话说，对于给定的输出样本块，二阶调制器更有效地利用其样本分配来表示输入。

图1.3.2a显示了通过级联两个DT积分器建立的二阶调制器，每个积分器从DAC接收加权反馈路径。系数通常称为积分标度或权重。在线性分析下，Z域的调制器输出产生:

(1.1)

其中代表量化器的增益。对于纯二阶整形，式(1)需要简化为

(1.2)

因此需要满足以下积分系数表达式：=1, =2 (1.3)

图1.3.2b显示了二阶SDM的替代表示，其允许分别使用系数和在每个积分器的前向和反馈路径中分配不同的权重。如图1.3.3所示，图1.3.2a和b中的符号可以利用下面等式连接：

,. (1.4)

图1.3.2a中的符号更接近调制器架构级，其中第一个积分器的传递函数为，第二阶积分器的传递函数为.而图1.3.2b中的符号更接近实际电路级实现，其中通常使用具有多个SC输入分支的积分器。后者有助于准确地说明实际SDM实现的一些非理想性。

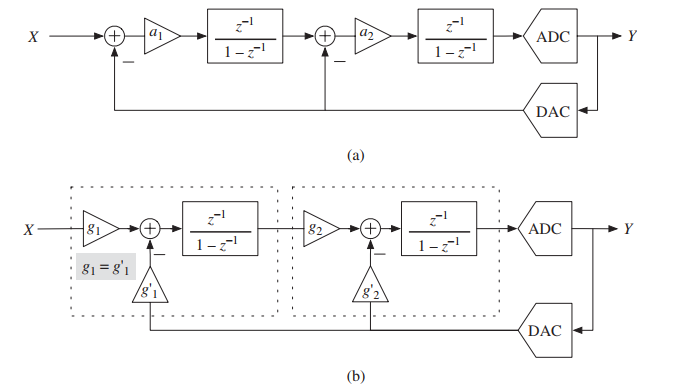
图1.3.2a 更接近调制器架构级的常用二阶SDM表示

图1.3.3(b)更接近实际电路级实现的二阶SDM表示

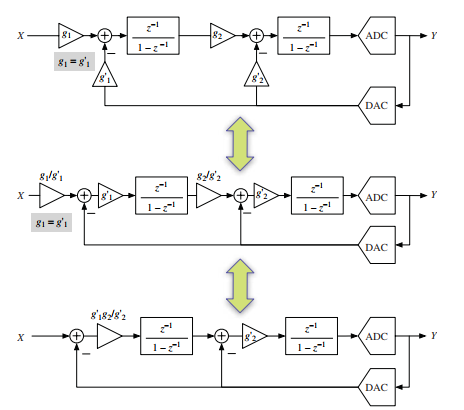
图1.3.3 图1.3.2a和1.3.2b中的DT表示之间的等效说明

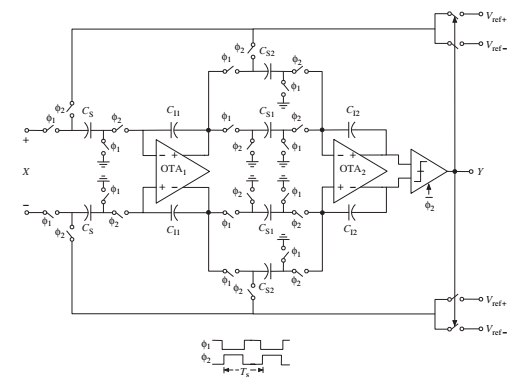
图1.3.4示出了使用全差分SC电路和假设单比特量化的图1.3.2中的二阶SDM的可能实现。调制器差分输入信号用X表示，调制器数字输出Y经比较器控制参考电压Vref+和Vref-到积分器的反馈连接。因此，调制器满标度范围等于2Vref，其中Vref=Vref+-Vref-。从图1.3.4中的第一个SC积分器注意到，调制器输入信号X和DAC反馈信号都通过采样电容进行处理，对于第二积分器，第一积分器的输出通过和处理，而DAC反馈信号仅通过处理. 因此，调制器标度系数被以下电容比实现：

，， (1.5)

若按照单端分析，

则得到

所以

1.3.4二阶SDM调制器的全差分SC实现

选择积分器权重的值不仅要满足等式1.3的关系，还要考虑到它们在调制器性能的一些方面中的含义。

保持状态变量（积分器输出）有界，以确保调制器的稳定性。如果>1.25，则不考虑量化器增益，二阶SDM对于范围为[-0.9∆/2，+0.9∆/2]的输入是稳定的。如果>2，则该条件已经满足，见方程式1.3和1.4。

保持调制器过载水平尽可能接近满标度，以确保高峰值信噪比SNR.

在积分器输出端最小化所需的信号范围；也就是说，积分器输出摆幅需求必须在预期的电压源下实现，并且尽可能低，以降低功耗并便于电路设计。

利用单位电容器比作为积分权的简化实现。

为了便于说明，表1.1显示了图1.3.2中为二阶单bit SDM报告的几组权重。所有机组均表现出过载水平XOL≈−4 dBFS（即比满标度振幅Vref=∆/2 低-4 dB），所需的积分器输出摆幅和最少单位电容数也包括在内。考虑了同一积分器中各权值间的电容分配问题。

表1.1二阶单比特M的一些系数集的比较

1.4多位Sigma-Delta调制

到目前为止，量化器和DAC是1位器件的调制器为1bit sigma-delta调制器。然而，使用多比特内部量化器的转换器提供了来自内部量化器的更多潜在分辨率。二阶多比特sigma-delta转换器看起来与图1.3.1所示的调制器完全相同，只是图中的e[n]将是n比特量化器而不是1比特量化器的模型，并且DAC将是n比特DAC而不是1比特DAC。多比特量化器的使用影响SNR表达式中的带N的项，其中，量化器中使用的每个附加比特将在SNR中产生6db的改进。在不使用近似值的情况下使用等式3，很容易看出，如果使用5位内部量化器而不是1位量化器，则SNR可以提高30db。或者，采样频率可以降低4倍，同时保持分辨率不变。

多比特sigma-delta系统的行为更接近线性化模型的预测（在极端情况下，如果量化器具有无限个比特，则不存在非线性）。因此，通常更准确地预测使用多比特量化器的高阶调制器的稳定性。另一种观察增强稳定性的方法是考虑多比特量化器的增益。如果使用midtread多比特量化器，其增益对于大多数输出值来说相对接近1（即使对于零输入，midtread量化器也将具有零输出，因此单位增益不同于midriser 1比特量化器，后者具有零输入的无限增益）。

使用多比特量化器的调制器与使用1比特内部量化器相比，主要缺点是不能在超大规模集成电路中容易地实现多位数模转换器，需要足够的线性度来实现高分辨率的转换。多位输出也使调制器后面的数字低通滤波器硬件复杂化，因为对于多位处理，滤波器需要多位硬件乘法器。

图1.41多比特SDM的线性模型，包括嵌入式ADC和DAC的误差

图1.41示出了多比特SDM的线性模型。与多比特转换相关的错误被添加到量化误差e中，该量化误差e已被考虑到；即，与A/D转换相关的错误和重建模拟所需的后续D/A转换中的错误反馈信号。注意，被注入到与量化误差e相同的路径中，因此，它也通过噪声整形在信号频带内衰减。然而，DAC误差被注入到反馈路径，因此，它被直接添加到SDM的输入，并作为输入信号本身的一部分传递到SDM输出。因此，多bit SDM的线性度将不比多位嵌入式DAC好，后者必须设计为实现整个sigma delta ADC的线性度目标，这在元件失配的影响下可能是一个挑战。

图1.42从概念上说明了通常用于SDM中的多位量化器的并行架构，其中分辨率通常较低（B≤5）。B位ADC由一组-1个比较器组成，比较器将环路滤波器输出数字化为thermometer code码，随后将其编码为二进制。DAC通过使用-1个单元元件（电容器、电阻器、电流源等，取决于电路实现）实现用个电平（从0到M=-1）重建模拟反馈信号。第i个模拟输出电平是通过激活第i个单元元件并添加其输出（电荷或电流）而产生的。DAC的误差是由其单元之间的不匹配引起的，这使得DAC的输出电平偏离其标称值。假设每个单元的实际值服从高斯分布，DAC输出的最坏相对误差可以估计为

式中，表示单位元件的相对误差。显然，由于采用了并行拓扑结构，DAC的精度随着单元元件的数量而增加。然而，对于具有4位嵌入量化以实现16位线性的SDM，DAC单元元件所需的匹配应优于0.01%（13位）。尽管如此，目前CMOS工艺中实现的器件匹配仍在0.1%（10位）的范围内，并且元件中所需的精度只能通过更多元件（64位）的并联来获得。这表明在多位SDM中，仅依靠标准器件匹配来获得优于12位或13位的线性度通常会导致禁止的区域占用。

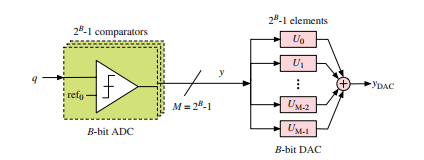
图1.42嵌入在M中的典型多位量化器的并行结构

1.4.1 DEM技术

如前所述，单元元件之间的不匹配导致DAC非线性，在SDM中产生谐波失真。对于图1.42结构，thermometric input code (y)和DAC输出（）的相应误差之间存在单声道对应关系，因为相同的单位元件总是用于生成给定的DAC输出电平。

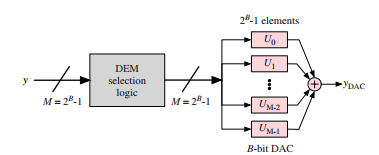
1.43结合元素选择逻辑将DEM应用于多位DAC

DEM的工作原理是打破这种直接对应关系，通过使生成给定DAC电平的元件随时间改变，从而将其固定误差转换为时变误差。为此，提出了图1.43中的概念，结合数字模块，根据一种算法来控制每个时钟周期的单元元件的选择，该算法试图使每个DAC电平随时间变化的平均误差为零。这样，位于低频范围的部分DAC误差功率将被推到更高的频率，并被抽取器移除。发展起来的大量实现DEM技术的算法可分为以下几类：

随机化算法:其中根据伪随机配置的网络（例如蝴蝶结构）选择DAC单元元件。将DAC产生的谐波失真转化为白噪声，通过抽取滤波器消除其带外功率。然而，信号频带内的DAC误差功率将增加SDM的噪声下限。

旋转算法，其中以周期方式选择DAC单元元件以将谐波失真移出信号频带。SDM的噪声下限没有增加，但信号处理可以产生在调制器通频带上折叠的混频分量。时钟平均（CLA）就是这种DEM技术的一个例

•失配整形算法是一种调整失配误差以将其大部分功率推到高频的算法，其中根据频率选择DAC单元元件。失配整形的顺序通常限制在一个或两个。单个电平平均（ILA）和数据加权平均（DWA）及其许多修改都与这类算法有关。

•矢量量化器结构结合，以实现高阶整形，其中误差反馈数字sigma delta转换器配置DWA和伪DWA算法。

1.5多级SDM

通过适当的标度系数，可以避免使用单回路SDM实现高阶NTF所产生的稳定性问题，但与理想的SDM相比，这导致DR显著降低。在所谓的级联SDM（也称为多环路SDMs或多级噪声成形（MASH）SDM）中发现了一种在避免不稳定性的同时获得高阶噪声成形的替代方法。其架构如图1.21所示，由N级调制器组成，其中每一级重新调制前一级中产生的量化误差的缩放值。级联级的输出可以方便地在数字域中进行处理，以在SDM的总输出y中抵消除后端级以外所有量化误差。另外，此外，后一量化误差出现在以L阶整形形成的级联输出上,其阶数L等于级联级的阶数总和（L＝L1+L2+···+LN）。无条件地，只要级联一阶和二阶SDM（≤2），就可以获得稳定的高阶整形，因为所有反馈回路都是低阶sigma delta级的局部反馈，并且没有级间反馈。因此，多级SDM的性能与理想的高阶单回路的性能相似，且不存在稳定性问题。

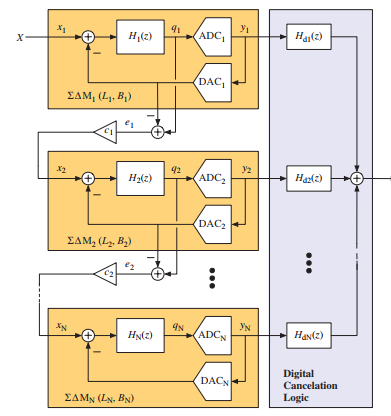
图1.21 N级级联SDM调制器的一般结构

通过级联两个一阶调制器获得的二级调制器的示例如图1.22所示，信号x[n]是级联中第一调制器的输入，但是第一调制器的量化误差[n]被用作第二调制器的输入。最后，第一级和第二级调制器的输出分别在经过数字延迟和数字微分器(1-)之后被添加到数字域中。

从用单位增益代替DAC的线性系统模型的Z域分析，我们得到:

输出计算为:

该和导致一阶噪声项的抵消以产生总输出.

除了与噪声无关的符号和输入所经历的额外延迟外，调制器实现与标准二阶sigma-delta调制器相同的输出。与二阶调制器相比，使用该结构的一个优点是，对于由±V限定的x[n]，一阶调制器部分中的任一部分中的量化器永远不会过载，级联结构要求模拟和数字传输函数之间的匹配，以及各级之间的D/A输出电平之间的匹配。事实上，失配效应和积分器泄漏会导致未整形或较差的整形噪声从早期部分传播到最终输出。

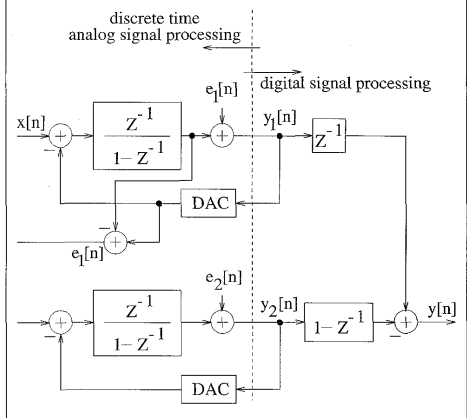
图1.22 两个一阶调制器级联获得的二级调制器

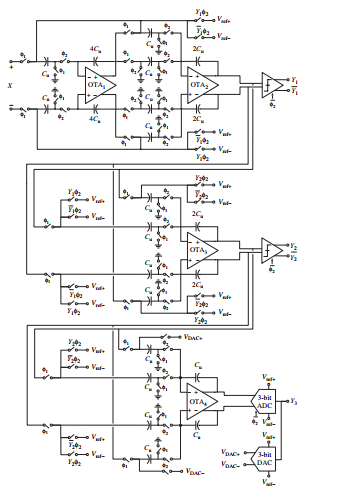
2-1-1多位调制器的全差分SC实现。

Sigma-delta转换器非常适合于信号带宽为4khz、分辨率为13-14位的语音应用。其中一个这样的转换器实际使用fs=4MHz的单比特一阶调制器或大约500倍的OSR来实现79db的动态范围，即大约13比特的分辨率。需要抖动来缓解与一阶调制器相关的音调问题。另一个转换器也使用fs=1.024MHz和128的OSR实现13位分辨率。所使用的调制器是采用1位量化器的标准二阶调制器。

2. 影响开关电容SDM性能的主要因素

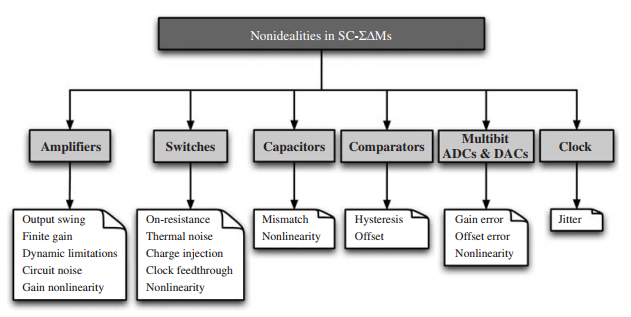
图2.1影响开关电容SDM性能的主要因素

2.1MOS开关电容电路

MOS工艺开关电容(SC)电路主要由MOS电容，时钟信号发生器，受时钟控制的MOS模拟开关，并配合以放大器或者运算器组成。

时钟信号

SC电路的时钟信号是由MOS数字电路产生，常用的时钟信号是两相不重叠的时钟信号，它们是一对互为反相的对称方波。如下图2.1(b)所示。

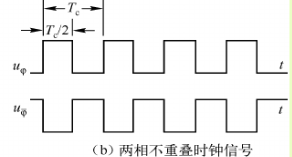
图2.1(b) 两相不重叠的时钟信号

开关电容单元

下图2.2(b)所示开关电容单元可以看作是两个图(a)所示开关电容单元的并联结构。当闭合时，,、, 当闭合时，,、在一个时钟周期内，电容、分别从端转向端转移的电荷量为:

-,-

在一个内经、从从端向端转移的总电荷量为：-

平均电流为:-,

等效电阻为，

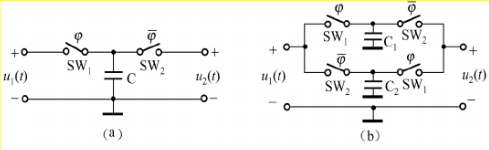
图2.2 开关电容单元

(1)开关电容的等效电阻与时钟频率有关，通过改变时钟顺率即可改变其等效电阻值，这对程控电阻、程控滤波器等都很有用

(3)时间常数是设计滤波器时必不可少的参数。等于电阻和电容的乘积，即=RC。因为集成电阻和电容的精度很差，绝对误差可达土20％，而且都随温度而变。如果用开关电容取代无源电阻R，则时间常数变为只与电容比值有关。=.

对开关电容电路进行分析时，可以利用电荷守恒原理，利用在不同时钟相的电荷总量相同。

2.1 SC-SDM中的有限放大器增益

在第一章中，考虑到理想SC-FE积分器的理想传递函数，推导了不同低通SC-SDM的理想性能:ITF(z)=

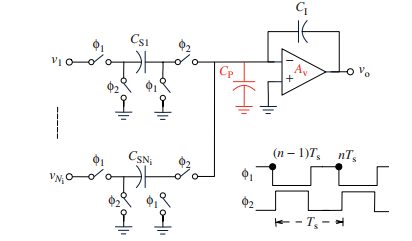
图2.2具有Ni个输入路径和有限放大器增益的SC-FE积分器

如图2.2所示，如果在SC-FE积分器的电荷转移中考虑了有限放大器增益和放大器求和节点处的寄生电容.

3.系统划分和抽象级别

图3.1b描述了SDMs设计中通常采用的分层综合方法。系统划分为以下层级[1–5]：

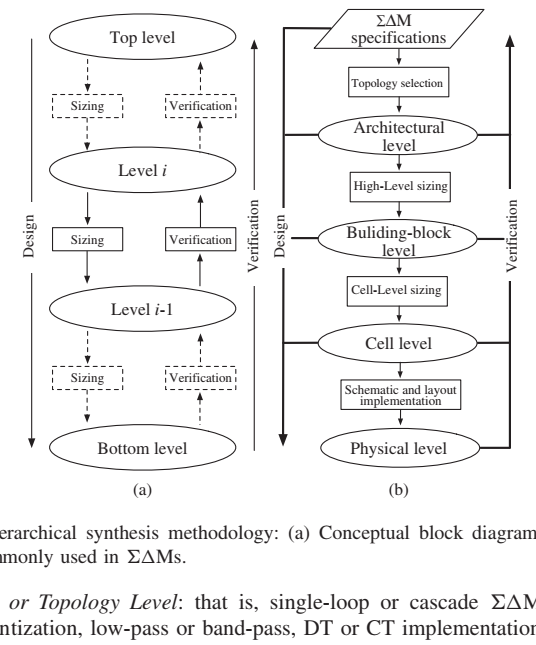
图3.1层次综合方法

(a)概念框图 (b) SDM中常用的系统划分。

Architecture or Topology Level(架构或拓扑级):单环或级联SDM,单bit或多bit量化、低通或带通、DT或CT实现等：

•Subcircuit or Building-Block Level(子电路或模块级)：即放大器、跨导、比较器、电容、电阻、开关等。

•Cell Level (单元级): 也就是说，给定模块的电路拓扑，例如折叠共源共栅或套筒共源共栅OTA、SC或电流控制DAC、NMOS或CMOS开关等.

•Physical Level(物理级实现)：从晶体管级原理图到布局和芯片实现。