研究了LCA，写篇笔记记录一下。

讲解使用例题 P3379 【模板】最近公共祖先（LCA）。

什么是LCA

最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。

—— 摘自 OI Wiki

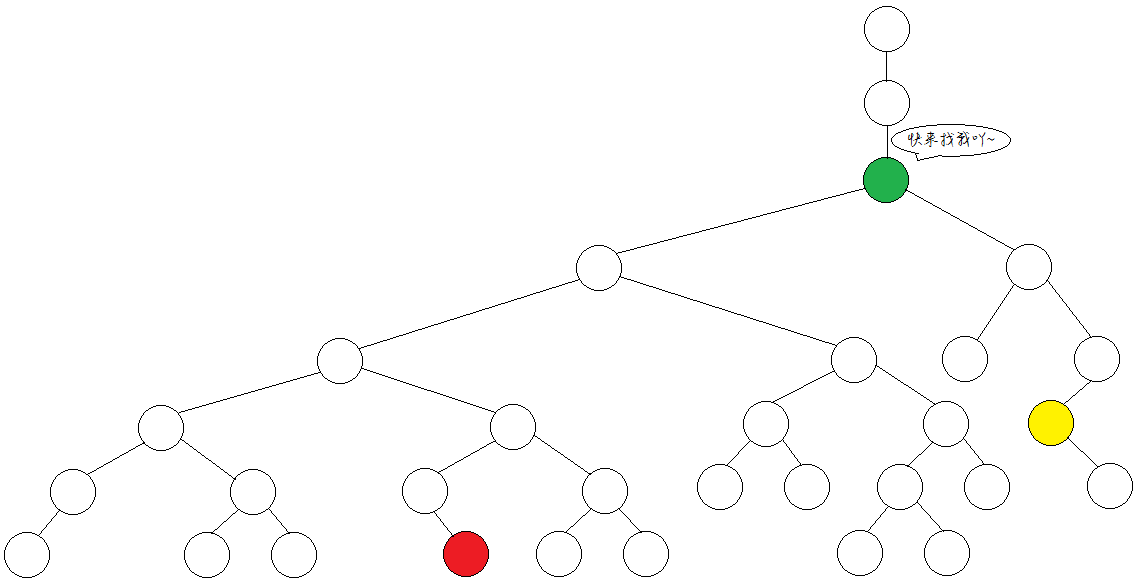
比如下图红、黄两点的LCA就是绿点。

LCA的几种实现方式

向上标记法

从 x 点一直向上走直到到达根节点，在走的过程中标记所有经过的点。

从 y 点一直向根节点走，遇到的第一个标记过的点即为两点的LCA。

代码略

树上倍增法

首先，我们将要求、lca的两点跳到同一深度，如下图：

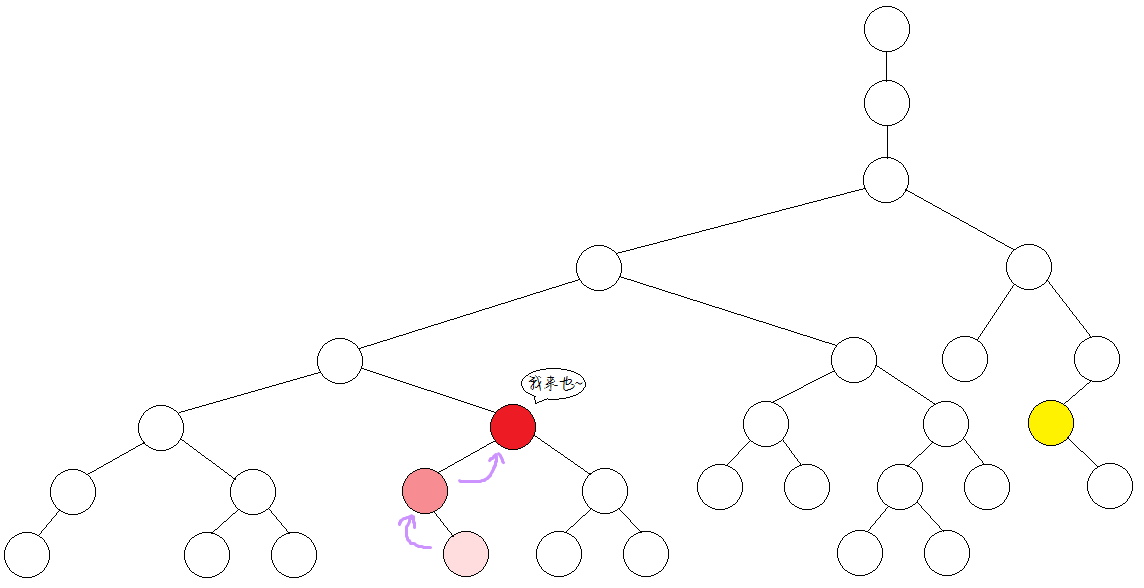
然后两点同时向上从大到小倍增，直到到的两点不相同，继续往上跳。

先尝试向能跳的最远处跳（4步）。

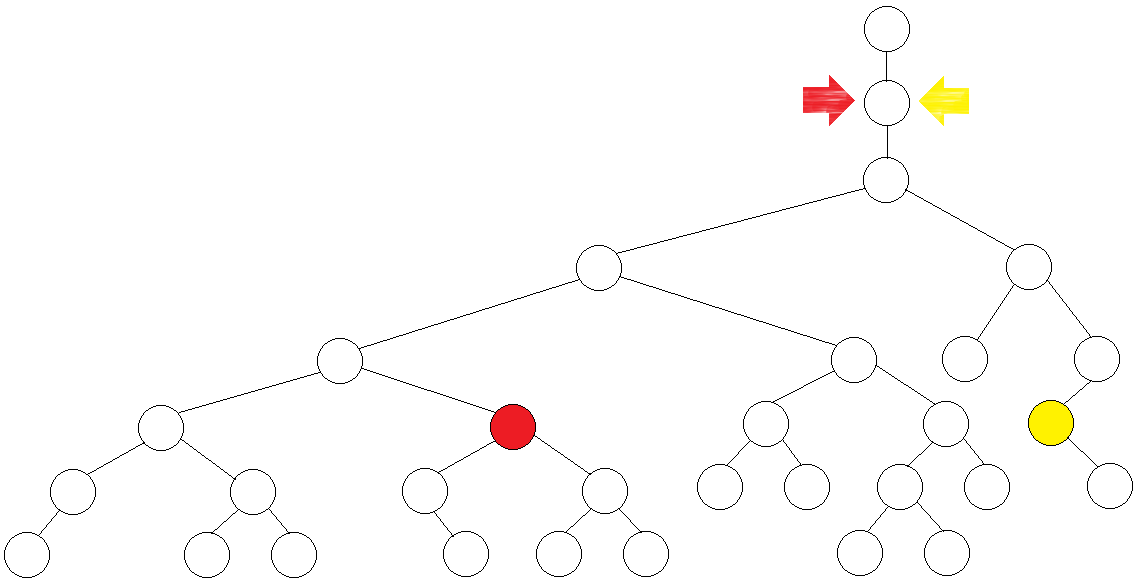
我们发现两个点在同处汇合，不行，考虑少跳一半（2步）。

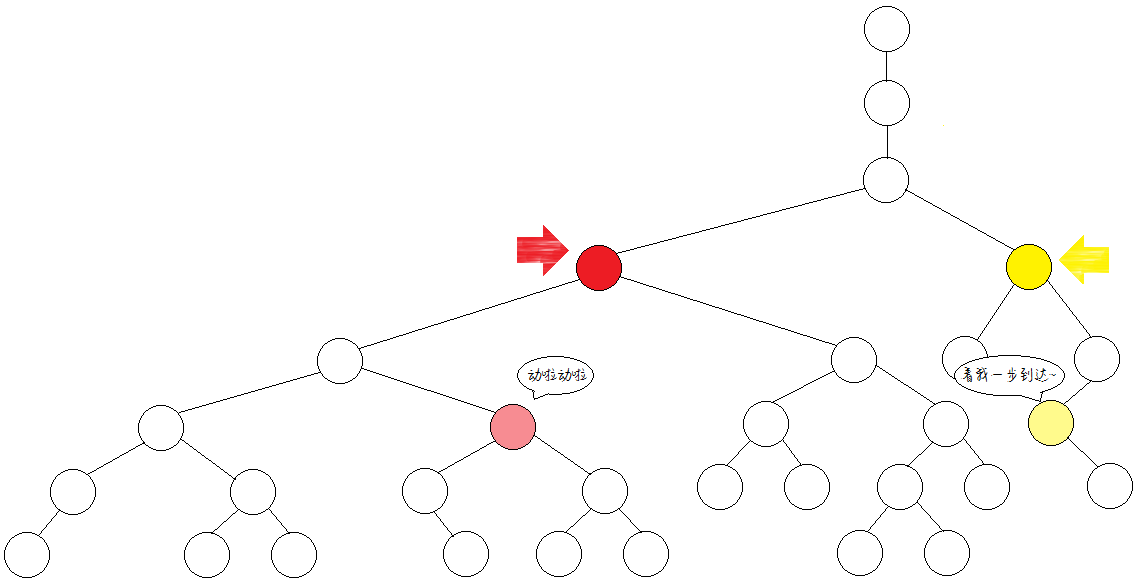
不同点，跳上。继续少跳一半（1步）。

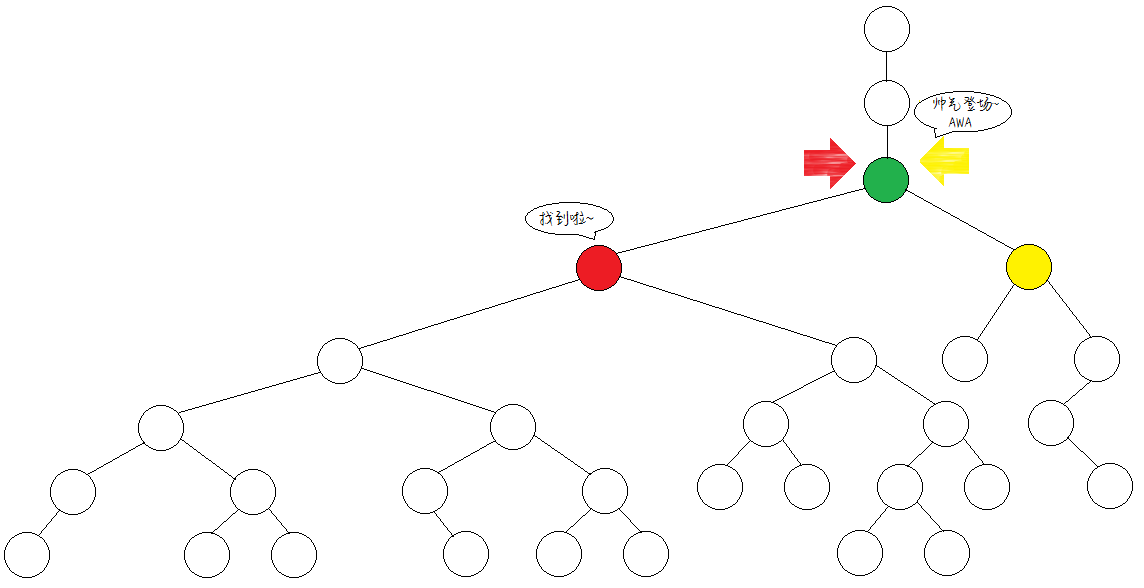
同一个点，不跳。

此时，所有的跳跃尝试结束。由于目前两点不在同处，故再往上跳一步。

于是就找到这两个点的LCA啦！

（是不是讲的云里雾里的，结合代码理解一下吧~）

代码实现

  • dfs获取每个点的深度
  1. int p[N], dep[N];
  2. void dfs(int x, int f) {
  3. 	p[x] = f;
  4. 	for (int i = last[x]; i; i = e[i].next) { //我用邻接表存的图
  5. 		int v = e[i].to;
  6. 		if (v == f) continue;
  7. 		dep[v] = dep[x] + 1;
  8. 		dfs(v, x);
  9. 	}
  10. }
  1. dep[s] = 1;
  2. dfs(s, s); //将起点的父节点设为自己，这样跳多了也不会出锅
  • 预处理倍增跳到的点
  1. for (int i = 1; i <= n; i++) f[0][i] = p[i];
  2. for (int j = 1; j <= lg; j++) // 跳 2^j 步   lg 为 log2(n)
  3. 	for (int i = 1; i <= n; i++) // 第 i 个点
  4. 		f[j][i] = f[j - 1][f[j - 1][i]];
  5. // 跳 2^j 步到的点即为先跳 2^(j-1) 步再跳 2^(j-1) 步到的点
  • 处理LCA

（没有写成函数QAQ）

  1. int a = read(), b = read();
  2. if (dep[a] > dep[b]) swap(a, b); //使 a 的深度小于等于 b
  3. for (int i = lg; i >= 0; i--)
  4. 	if (dep[f[i][b]] >= dep[a]) b = f[i][b]; //将 a 与 b 跳到同一深度
  5. for (int i = lg; i >= 0; i--) //从最远的距离开始尝试 （跳 2^i 步）
  6. 	if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a]; //不是同一个点就跳上去
  7. if (a != b) a = p[a];
  8. //结束后不是同一个点，那么LCA就是目前这个点的父节点，所以也可以写成 b = p[b] 然后输出 b
  9. printf("%d\n", a);
  • 为什么尝试跳只用从 log2(n) 循环一遍到 0 就行？

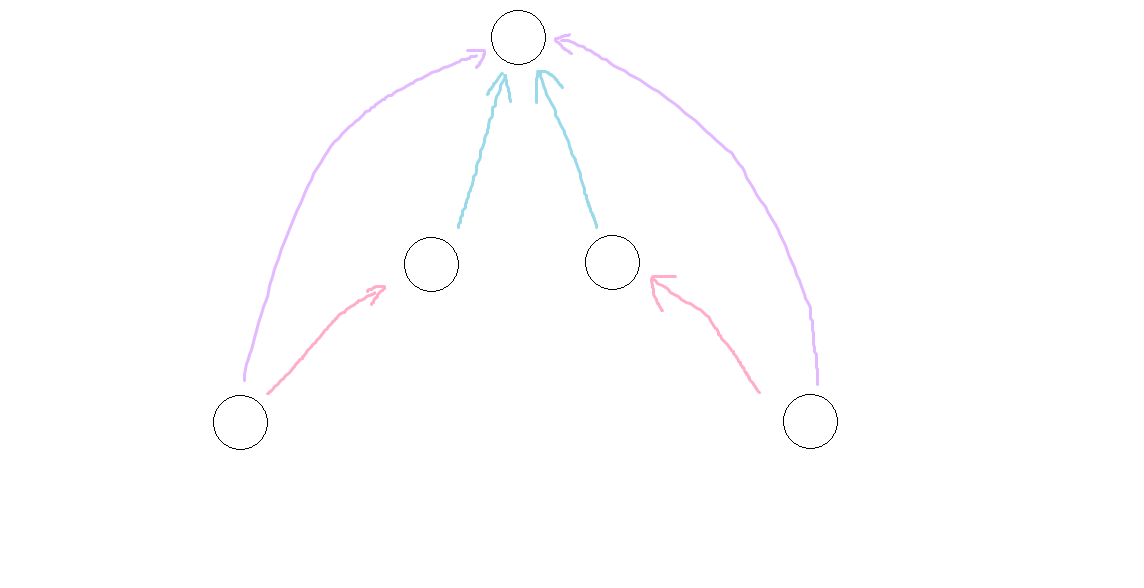
按照代码思路，我们会先尝试沿紫色路径跳 2^j 步，由于不成功，我们折半跳 2^(j-1) 步，沿粉边跳上。

此时若在沿蓝边跳 2^(j-1) 步，又跳到了原来粉边指向的点，我们已经知道那个点不行，所以不用尝试跳上，而应该继续尝试跳 2^(j-2) 步。

完整代码（点击查看） 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define ll long long
  4. inline ll read() {
  5. 	ll s = 0, w = 1;
  6. 	char ch = getchar();
  7. 	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
  8. 	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
  9. 	return s * w;
  10. }
  11. const int N = 500010;
  12. int n, m, s;
  13. int last[N], cnt;
  14. struct edge {
  15. 	int to, next;
  16. } e[N << 1];
  17. void addedge(int x, int y) {
  18. 	e[++cnt].to = y;
  19. 	e[cnt].next = last[x];
  20. 	last[x] = cnt;
  21. }
  22. int p[N], dep[N];
  23. void dfs(int x, int f) {
  24. 	p[x] = f;
  25. 	for (int i = last[x]; i; i = e[i].next) {
  26. 		int v = e[i].to;
  27. 		if (v == f) continue;
  28. 		dep[v] = dep[x] + 1;
  29. 		dfs(v, x);
  30. 	}
  31. }
  32. int f[19][N], lg;
  33. int main() {
  34. 	n = read(), m = read(), s = read();
  35. 	lg = log2(n);
  36. 	for (int i = 1; i < n; i++) {
  37. 		int u = read(), v = read();
  38. 		addedge(u, v), addedge(v, u);
  39. 	}
  40. 	dep[s] = 1;
  41. 	dfs(s, s);
  42. 	for (int i = 1; i <= n; i++) f[0][i] = p[i];
  43. 	for (int j = 1; j <= lg; j++)
  44. 		for (int i = 1; i <= n; i++)
  45. 			f[j][i] = f[j - 1][f[j - 1][i]];
  46. 	while (m--) {
  47. 		int a = read(), b = read();
  48. 		if (dep[a] > dep[b]) swap(a, b);
  49. 		for (int i = lg; i >= 0; i--)
  50. 			if (dep[f[i][b]] >= dep[a]) b = f[i][b];
  51. 		for (int i = lg; i >= 0; i--)
  52. 			if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a];
  53. 		if (a != b) a = p[a];
  54. 		printf("%d\n", a);
  55. 	}
  56. 	return 0;
  57. }

LCA的Tarjan算法

本质来说，其实就是用并查集对“向上标记法”进行优化。

注意：操作是离线的。

从根节点开始进行 DFS，对于每个搜到的点打上标记，在回溯时将该结点并入其父节点的集合，具体操作见下。

  • 如何离线？

我们先把 m 次询问都读入，然后再相关的两个结点上分别挂上询问。

  • 为什么要两点都挂上询问

因为我们并不知道两个点谁先访问谁后访问，不好处理。

比如现在给一棵树，询问红、黄两点的 LCA 。

我们对这棵树进行 DFS，目前已经搜到了黄点，上方的三个不同深度的橙点表示 DFS 过程中栈里的点。

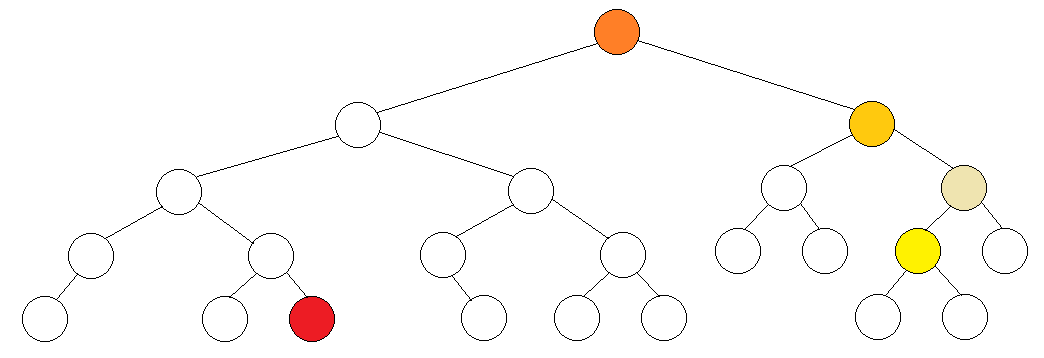
由于已经搜过了根节点的左子树，所以红点已打过标记。根节点的左子树与根节点属于一个集合，第二层的黄点的左子树与它自己属于一个集合。

现在在黄点上打个标记，发现黄点上挂的关于红点的询问可以处理了（两点都已搜到）。

红、黄两点的LCA即为红点所在集合的根节点，即图中树的根节点。

（讲的有亿点点乱诶）

代码实现

  • 存储询问
  1. struct node { //为了保证输出顺序，不仅要把询问挂在点上，还要额外存一下
  2. 	int x, y, ans;
  3. } ask[N];
  4. vector <int> g[N]; //每个点上挂的询问
  1. for (int i = 1; i <= m; i++) {
  2. 	ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
  3. 	g[ask[i].x].push_back(i);
  4. 	g[ask[i].y].push_back(i);
  5. }
  • DFS
  1. int p[N];
  2. bool vis[N]; //访问标记
  3. int r[N]; //一个集合实际的根节点（并查集是按秩合并的，根节点不能保证是我们要的根节点）
  4. void dfs(int x, int f) {
  5. 	p[x] = f;
  6. 	for (int i = last[x]; i; i = e[i].next) {
  7. 		int v = e[i].to;
  8. 		if (v == f) continue;
  9. 		vis[v] = 1;
  10. 		for (int j : g[v]) { //遍历所有询问
  11. 			int o = ask[j].x;
  12. 			if (o == v) o = ask[j].y;
  13. 			if (!vis[o]) continue;
  14. 			ask[j].ans = r[a.root(o)]; //记录询问答案
  15. 		}
  16. 		dfs(v, x);
  17. 		a.merge(x, v); //合并两个集合
  18. 		r[a.root(x)] = x; //标记实际根节点
  19. 	}
  20. }
  1. vis[s] = 1;
  2. dfs(s, s);
完整代码（点击查看） 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define ll long long
  4. inline ll read() {
  5. 	ll s = 0, w = 1;
  6. 	char ch = getchar();
  7. 	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
  8. 	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
  9. 	return s * w;
  10. }
  11. const int N = 500010;
  12. int n, m, s;
  13. struct Disjoint_Set {
  14. 	int p[N], size[N];
  15. 	void build() {
  16. 		for (int i = 1; i <= n; i++) p[i] = i, size[i] = 1;
  17. 	}
  18. 	int root(int x) {
  19. 		if (p[x] != x) return p[x] = root(p[x]);
  20. 		return x;
  21. 	}
  22. 	void merge(int x, int y) {
  23. 		x = root(x), y = root(y);
  24. 		if (size[x] > size[y]) swap(x, y);
  25. 		p[x] = y;
  26. 		size[y] += size[x];
  27. 	}
  28. 	bool check(int x, int y) {
  29. 		x = root(x), y = root(y);
  30. 		return x == y;
  31. 	}
  32. } a;
  33. int last[N], cnt;
  34. struct edge {
  35. 	int to, next;
  36. } e[N << 1];
  37. void addedge(int x, int y) {
  38. 	e[++cnt].to = y;
  39. 	e[cnt].next = last[x];
  40. 	last[x] = cnt;
  41. }
  42. struct node {
  43. 	int x, y, ans;
  44. } ask[N];
  45. vector <int> g[N];
  46. int p[N];
  47. bool vis[N];
  48. int r[N];
  49. void dfs(int x, int f) {
  50. 	p[x] = f;
  51. 	for (int i = last[x]; i; i = e[i].next) {
  52. 		int v = e[i].to;
  53. 		if (v == f) continue;
  54. 		vis[v] = 1;
  55. 		for (int j : g[v]) {
  56. 			int o = ask[j].x;
  57. 			if (o == v) o = ask[j].y;
  58. 			if (!vis[o]) continue;
  59. 			ask[j].ans = r[a.root(o)];
  60. 		}
  61. 		dfs(v, x);
  62. 		a.merge(x, v);
  63. 		r[a.root(x)] = x;
  64. 	}
  65. }
  66. int main() {
  67. 	n = read(), m = read(), s = read();
  68. 	a.build();
  69. 	for (int i = 1; i <= n; i++) {
  70. 		r[i] = i;
  71. 	}
  72. 	for (int i = 1; i < n; i++) {
  73. 		int u = read(), v = read();
  74. 		addedge(u, v), addedge(v, u);
  75. 	}
  76. 	for (int i = 1; i <= m; i++) {
  77. 		ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
  78. 		g[ask[i].x].push_back(i);
  79. 		g[ask[i].y].push_back(i);
  80. 	}
  81. 	vis[s] = 1;
  82. 	dfs(s, s);
  83. 	for (int i = 1; i <= m; i++) printf("%d\n", ask[i].ans);
  84. 	return 0;
  85. }

LCA转RMQ

先贴代码吧，讲解后续再补

咕咕咕

完整代码（点击查看） 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define ll long long
  4. inline ll read() {
  5. 	ll s = 0, w = 1;
  6. 	char ch = getchar();
  7. 	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
  8. 	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
  9. 	return s * w;
  10. }
  11. const int N = 500010;
  12. int n, m, s;
  13. int last[N], cnt;
  14. struct edge{
  15. 	int to, next;
  16. } e[N << 1];
  17. void addedge(int x, int y) {
  18. 	e[++cnt].to = y;
  19. 	e[cnt].next = last[x];
  20. 	last[x] = cnt;
  21. }
  22. int dep[N], a[N << 1], ed, fst[N];
  23. void dfs(int x, int f) {
  24. 	a[++ed] = x;
  25. 	if (!fst[x]) fst[x] = ed;
  26. 	for (int i = last[x]; i; i = e[i].next) {
  27. 		int v = e[i].to;
  28. 		if (v == f) continue;
  29. 		dep[v] = dep[x] + 1;
  30. 		dfs(v, x);
  31. 		a[++ed] = x;
  32. 	}
  33. }
  34. int f[21][N << 1], lg;
  35. int main() {
  36. 	n = read(), m = read(), s = read();
  37. 	lg = log2(n) + 1;
  38. 	for (int i = 1; i < n; i++) {
  39. 		int x = read(), y = read();
  40. 		addedge(x, y), addedge(y, x);
  41. 	}
  42. 	dep[s] = 1;
  43. 	dfs(s, s);
  44. 	for (int i = 1; i <= ed; i++) f[0][i] = i;
  45. 	for (int j = 1; j <= lg; j++) {
  46. 		for (int i = 1; i <= ed - (1 << j) + 1; i++) {
  47. 			int i2 = i + (1 << (j - 1));
  48. 			if (dep[a[f[j - 1][i]]] < dep[a[f[j - 1][i2]]]) f[j][i] = f[j - 1][i];
  49. 			else f[j][i] = f[j - 1][i2];
  50. 		}
  51. 	}
  52. 	for (int i = 1; i <= m; i++) {
  53. 		int x = read(), y = read();
  54. 		if (fst[x] > fst[y]) swap(x, y);
  55. 		int len = fst[y] - fst[x] + 1, ans;
  56. 		int lg2 = log2(len);
  57. 		int i2 = fst[y] - (1 << lg2) + 1;
  58. 		if (dep[a[f[lg2][fst[x]]]] < dep[a[f[lg2][i2]]]) ans = a[f[lg2][fst[x]]];
  59. 		else ans = a[f[lg2][i2]];
  60. 		printf("%d\n", ans);
  61. 	}
  62. 	return 0;
  63. }

最近公共祖先（LCA）学习笔记 | P3379 【模板】最近公共祖先（LCA）题解的更多相关文章

  1. OpenCV 学习笔记（模板匹配）

    OpenCV 学习笔记(模板匹配) 模板匹配是在一幅图像中寻找一个特定目标的方法之一.这种方法的原理非常简单,遍历图像中的每一个可能的位置,比较各处与模板是否"相似",当相似度足够 ...

  2. Python Flask学习笔记之模板

    Python Flask学习笔记之模板 Jinja2模板引擎 默认情况下,Flask在程序文件夹中的templates子文件夹中寻找模板.Flask提供的render_template函数把Jinja ...

  3. poj1330 lca 最近公共祖先问题学习笔记

    首先推荐两个博客网址: http://dongxicheng.org/structure/lca-rmq/ http://scturtle.is-programmer.com/posts/30055. ...

  4. Angular 5.x 学习笔记(1) - 模板语法

    Angular 5.x Template Syntax Learn Note Angular 5.x 模板语法学习笔记 标签(空格分隔): Angular Note on github.com 上手 ...

  5. LCA学习笔记

    写在前面 目录 一.LCA的定义 二.暴力法求LCA 三.倍增法求LCA 四.树链剖分求LCA 五.LCA典型例题 题目完成度 一.LCA的定义 LCA指的是最近公共祖先.具体地,给定一棵有根树,若结 ...

  6. 倍增求LCA学习笔记（洛谷 P3379 【模板】最近公共祖先（LCA））

    倍增求\(LCA\) 倍增基础 从字面意思理解,倍增就是"成倍增长". 一般地,此处的增长并非线性地翻倍,而是在预处理时处理长度为\(2^n(n\in \mathbb{N}^+)\ ...

  7. LCA 学习算法 （最近的共同祖先）poj 1330

    Nearest Common Ancestors Time Limit: 1000MS   Memory Limit: 10000K Total Submissions: 20983   Accept ...

  8. 倍增LCA学习笔记

    前言 ​ "倍增",作为一种二进制拆分思想,广泛用于各中算法,如\(ST\)表,求解\(LCA\)等等...今天,我们仅讨论用该思想来求解树上两个节点的\(LCA\)(最近公共祖先 ...

  9. leetcood学习笔记-14*-最长公共前缀

    笔记: python if not   判断是否为None的情况 if not x if x is None if not x is None if x is not None`是最好的写法,清晰,不 ...

随机推荐

  1. .netcore6.0自己配置swagger

    环境:.net core6.0 一.安装依赖包:Swashbuckle.AspNetCore 二.右击项目->属性->生成->输出,勾选文档文件,然后配置文件生成路径,注意是相对路径 ...

  2. elasticsearch-spark的用法

    Hadoop允许Elasticsearch在Spark中以两种方式使用:通过自2.1以来的原生RDD支持,或者通过自2.0以来的Map/Reduce桥接器.从5.0版本开始,elasticsearch ...

  3. 浅析kubernetes中client-go Informer

    之前了解了client-go中的架构设计,也就是 tools/cache 下面的一些概念,那么下面将对informer进行分析 Controller 在client-go informer架构中存在一 ...

  4. Spark: 单词计数(Word Count)的MapReduce实现(Java/Python)

    1 导引 我们在博客<Hadoop: 单词计数(Word Count)的MapReduce实现 >中学习了如何用Hadoop-MapReduce实现单词计数,现在我们来看如何用Spark来 ...

  5. github新项目npm错误

    当我们从GitHub或者别人那里拿到项目的时候,一般都是要先npm install 进行安装依赖.但是难免会遇到报错. 出现问题1: 解决方案:清除缓存npm cache clear --force之 ...

  6. python和numpy中sum()函数的异同

    转载:https://blog.csdn.net/amuchena/article/details/89060798和https://www.runoob.com/python/python-func ...

  7. 使用kubeseal加密和管理k8s集群的secret

    使用kubeseal加密和管理k8s集群的secret 在k8s的管理过程中,像secret这种资源并不好维护,kubeseal提供了一种相对简单的方式来对原始secret资源进行加密,并通过控制器进 ...

  8. camunda开源流程引擎的数据库表结构介绍

    Camunda bpm流程引擎的数据库由多个表组成,表名都以ACT开头,第二部分是说明表用途的两字符标识.本文以Camunda7.11版本为例,共47张表. ACT_RE_*: 'RE'表示流程资源存 ...

  9. vue华视电子身份证阅读器的使用

          ie还是谷歌都是可以用的 只需要直接启用华视电子身份证阅读器的服务来的,至于服务已经上传到了网上   华视阅读器服务,下载下来解压,找到对应的华视电子读卡服务.exe文件,路径是CVR-1 ...

  10. Obsidian基础教程

    Obsidian基础教程 相关链接 2021年新教程 - Obsidian中文教程 - Obsidian Publish 软通达 基础设置篇 1. 开启实时预览 开启实时预览模式,所见即所得 打开设置 ...