PKUSC 2022 口胡题解

\(PKUSC\ 2022\)口胡题解

为了更好的在考试中拿分,我准备学习基础日麻知识(为什么每年都考麻将 啊啊啊)

首先\(STO\)吉老师\(ORZ,\)真的学到了好多

观察标签发现,这套题覆盖知识点广,难度适中,是一套不可多得的题

\(DAY1\)

\(T1\)

考虑过程必然是,一个值小的在参加若干轮之后超过大的,然后目前值小的参加若干轮依次交替

首先考虑单个变量

我们枚举\(i\)向后跳的第一步,假设跳到\(i-j,\)然后后面的过程是

\(i->j\)表示进行若干轮之后,中间过程不超过\(i,\)最后一次直接到\(j\)

\(i->^{k}j\)表示\(i\)进行若干轮到\(j,\)中间过程在\([i,j]\)之间到的第一个数是\(k\)

\(x_{st}=i-j,x_{ed}=i+k\)

\(Sit_1:\)我们过程中没经过\(i-j+1 ...i\)里面的位置,等价于事件\(i-j->i+k\)

\(Sit_2:\)我们过程中经过了\(i-j+1 ...j,\)可以拆分为事件\(i-j->l\)和事件\(l->^i i+k\)

得到如下递推式

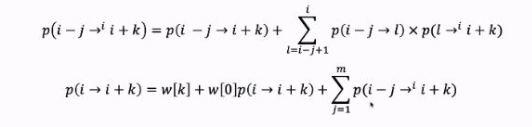
\(i\)从小到大计算\(p(i->i+k)\)

\(j\)从小到大计算\(p(i-j->^i i+k)\)

解方程得到\(p(i->i+k)\)

然后我们两个变量,设\((i,j)\)表示较大值为\(i,\)较小值为\(i-j\)

然后枚举\(k\)第一个大于\(i-j\)的值

\(k<=i,(i,j)->(i,i-k)\)

\(k>i,(i,j)->(k,k-)\)

复杂度\(O(nm^3)\)

\(T2\)

很\(nb\)的数据结构\(+\)容斥

其实\(sub_4\)已经极大提示了正解

我们能贡献的线段全部用颜色标出来,我们的贡献大概分成这几种类型

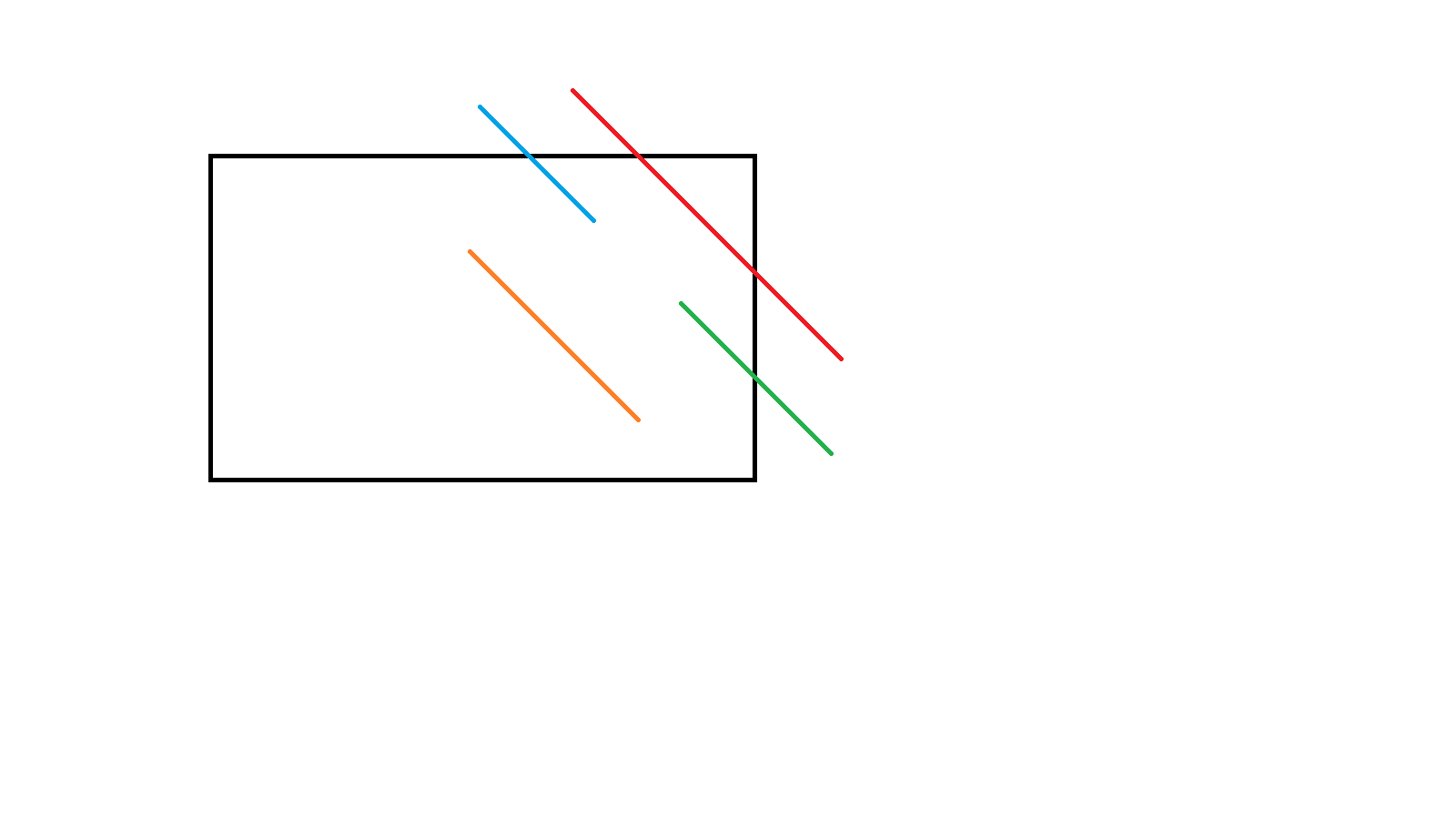
我们可以使用容斥,\(Sum-out,\)对于\(out\)我们只需要对于\(x,y\)分别维护两棵线段树使用扫描线解决

在\(x,y\)轴的线段树维护区间和(区间和乘导数)就很容易得到了

那么我们的正解只需要得到一个恰当的扫描序列,然后和\(sub_4\)一样做法,可以使用平衡树\((set)\)得到序列

这个序列保证了在询问后面的线段一定不会贡献,那么\(Sum\)一定不会算进去后面的线段,前面的线段直接扫描线即可

\(T3\)

最最基础的暴力分,可以二分答案\(+\)线性规划(单纯形随便跑)

最基础的暴力分,可以二分答案\(+\)网络流

正解,我们只需要找到一个能流满的最大流即可,使用\(Hall\)引理(我\(TM\)原来没听过,貌似全机房都不会,那没事了)

\(Hall\)引理(二分图存在完美匹配的充分必要条件)

对于右部点所有子集,\(Sum(left->x)>=Need(x),\)我们对于所有的式子求一个\(Min\)即可

---

\(DAY2\)

\(T1\)

当我看到第一个式子的时候就半掉线了

大概听懂了\(70\%\)

放上\(sol\)截图,我大概是胡不出来了

大概是一个转化成二分图求联通块方案数的问题

复杂度\(O(n^6)\)

\(T2\)

首先,这题怎么想都不会想到是随机,啊啊啊

首先对于颜色\(x\)的边共\(Num_x\)条,前\(Num_x-1\)条随机赋值,最后一条为前\(Num_x-1\)条的异或值

首先如果一条路径的异或和为\(0,\)大概率把包含的颜色所有边都包含了(为什么是大概率,可能会出现,两个不同颜色的边都不是\(0,\)异或出来\(0\),我们只需要\(mt19937(time(0))\)多次提交(看运气能否在\(32\)发以内\(AC\))即可

我们设\(v_i\)为\(1->i\)的路径权值,\(v_i\ xor\ v_j\)比较显然的是\(i->j\)路径的异或和,我们只需要对于\(v_i\)相同的求一个路径最长的即可

题目说了对于删点之后的操作,先求出最长路径,最最长路径外面的点答案必然是\(Max,\)内部的点\(x\),贡献可以分为,左边过来的,右边过来的,子树内部即可

然后我们最长路径从左往右扫一遍,从右往左扫一遍,维护一个可插入的数据结构,每个点都查询一下左右最大值即可

\(T3\)

比较套路的思路,比较套路的\(dp\)状态,基本上可以参考近几年的麻将题的\(dp\)思路

甚至可以搜索

吉老师\(:\)我们暴力搜索通过前\(3\)个\(sub\)的同学加了卡时之后可以获得前\(4\)个\(sub\),而我们暴力搜索通过前\(4\)个\(sub\)的同学可以通过增加卡时获得\(AC\)

。。。。。。。。。。。我会了,以后一定写卡时