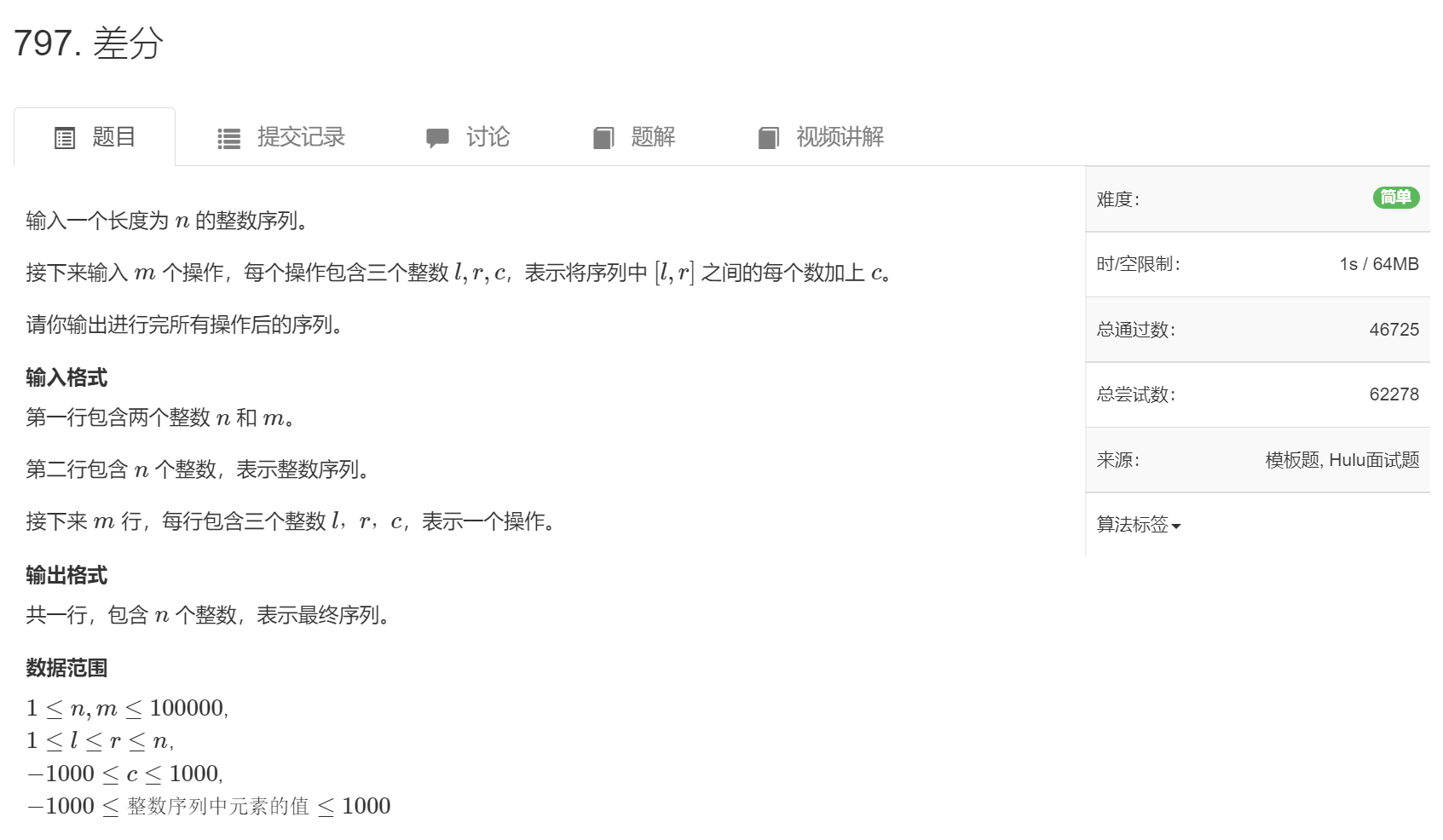
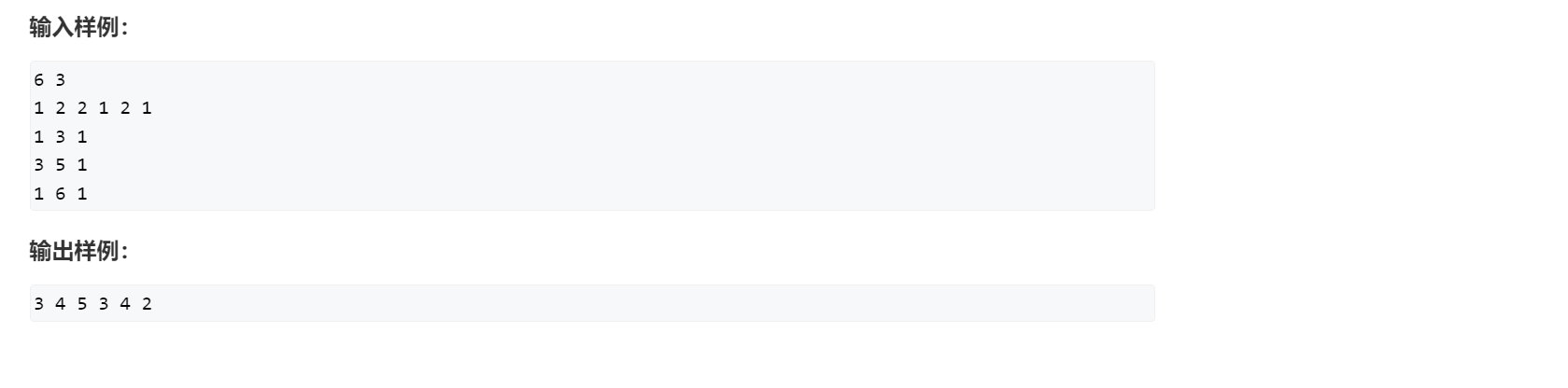
[AcWing 797] 差分

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}
int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i ++)   scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++)   insert(i, i, a[i]);
    while (m --) {
        int l, r, c;
        scanf("%d %d %d", &l, &r, &c);
        insert(l, r, c);
    }
    for (int i = 1; i <= n; i ++)   b[i] += b[i - 1];
    for (int i = 1; i <= n; i ++)   printf("%d ", b[i]);
    return 0;
}

---

1. 不需要考虑怎么构造，只需要考虑怎么插入；
2. b[ i ] 是 a[ i ] 的差分，a[ i ] 是 b[ i ] 的前缀和，b[ i ] = a[ i ] - a[ i - 1 ]；
3. insert 函数的作用为，让 b[ l ] 到 b[ r ] 每一个数都加上 c，使用 insert 把 a[ i ] 插入到 b[ i ] 的位置，在后面每次读入 l, r, c 后，用 insert 函数对 b 进行操作；
4. 对 b 进行求前缀和的操作是， b[ i ] += b[ i - 1 ]，不断累加，b[ i ] 就变为了前缀和，也就是最终序列；