广州2022CCPC补题

I Infection

知识点: 树上背包

第一次写树上背包的题目，没想到就是在区域赛中

神奇的是树上背包的复杂度，看起来是\(O(n^3)\)，但是实际计算只有\(O(n^2)\)

学会树上背包后可以很明显^[1]的发现这是一道树上背包的题目

而我认为该题思路的难点^[2]在于想到先枚举被感染的点集，再确定起始感染点是哪一个

所以我们就可以定义dp状态：

1.该点集是否包含起始感染点

2.以u为根的子树

3.该点集内被感染的点数

如果已经学过树上背包，此时就十分好转移了

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;

const int mod = 1e9 + 7;
const int N = 2e3 + 5;

ll dp[2][N][N];

ll ksm(ll x, int n)
{
    ll ret = 1;
    while (n)
    {
        if (n & 1) ret = ret * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return ret;
}
vc<int> h[N];
ll p[N], w[N], ans[N];
int sz[N];

void dfs(int u, int fa)
{
    dp[0][u][0] = 1 - p[u]; //未选择初始感染点,u子树,0个感染点
    dp[0][u][1] = p[u];     //未选择初始感染点,u子树,1个感染点
    dp[1][u][1] = w[u];     //选择u为初始感染点,1个感染点

    sz[u] = 1;  //已合并节点个数

    for (auto v : h[u])
    {
        if (v == fa) continue;
        dfs(v, u);

        vc<ll> dp0(sz[u] + sz[v] + 1, 0), dp1(sz[u] + sz[v] + 1, 0);
        rep(i, 1, sz[u]) rep(j, 0, sz[v])
        {
            dp0[i + j] = (dp0[i + j] + dp[0][u][i] * dp[0][v][j]) % mod;
            dp1[i + j] = (dp1[i + j] + dp[1][u][i] * dp[0][v][j] + dp[0][u][i] * dp[1][v][j]) % mod;
        }
        sz[u] += sz[v];
        //更新dp状态
        rep(i, 1, sz[u])
        {
            dp[0][u][i] = dp0[i];
            dp[1][u][i] = dp1[i];
        }
    }
    //统计答案
    rep(i, 1, sz[u]) ans[i] = (ans[i] + dp[1][u][i] * (1 - p[fa])) % mod;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    //init
    int n; cin >> n;
    rep(i, 2, n)
    {
        int u, v; cin >> u >> v;
        h[u].push_back(v);
        h[v].push_back(u);
    }
    ll wi(0);
    rep(i, 1, n)
    {
        int a, b, c;
        cin >> a >> b >> c;
        wi += w[i] = a;
        p[i] = b * ksm(c, mod - 2) % mod;
    }
    wi = ksm(wi, mod - 2);
    rep(i, 1, n) w[i] = w[i] * wi % mod;

    //树上背包
    dfs(1, 0);

    //输出答案
    rep(i, 1, n) cout << (ans[i] % mod + mod) % mod << endl;
    return 0;
}

---

M XOR Sum

知识点: 数位dp

赛时属于是被1e15，1e13这么大的数据范围吓到了

赛后看到了枚举余数后立马想到了累计高位余数

不过我只能想到\(9×9=81\)，以为对高位影响最多40

于是就写成了\(dp[45] [20] [45]\)，被学长一眼看出不妥

高位余数至少需要\(80+40+20+10+5+2+1=158\)

所以要开\(dp[45] [20] [175]\)，所以电子竞技菜是原罪

该题思维的难点在于如何处理如此巨大的 \(n\) ，

而看出通过计算高位余数后，如何处理异或和数位dp就变得十分显然

dp写法

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;

const int mod = 1e9 + 7;
const int FN = 25;
ll fac[FN];//阶乘数组
ll ifc[FN];//阶乘逆元
ll inv[FN];//逆元

void init(int n)
{
    fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
    rep(i, 2, n)
    {
        fac[i] = fac[i - 1] * i % mod;
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
        ifc[i] = ifc[i - 1] * inv[i] % mod;
    }
}

ll C(ll n, ll m)
{
    if (n < m) return 0;
    return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}

ll n, m, k;
ll dp[45][20][175];
int lim[45];

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m >> k;
    init(22);   //预处理组合数
    rep(i, 0, 40) lim[i] = (m >> i) & 1; //二进制拆分m
    memset(dp, -1, sizeof(dp));
    if ((n >> 41) > 170)
    {
        cout << 0 << endl;
        return 0;
    }
    dp[41][k][n >> 41] = 1;
    per(i, 41, 1) rep(j, 0, k) rep(t, 0, 170)
    {
        ll &u = dp[i][j][t];                    //当前状态
        if (u < 0) continue;                    //如果当前状态没被枚举过就跳过
        int sum = t * 2 + ((n >> (i - 1)) & 1); //上一位遗留来的余数
        if (lim[i - 1] == 0)                    //当前上界为0
        {
            rep(x, j, k)
            {
                if (x * (k - x) > sum) continue;        //总和n被超过
                if (sum - x * (k - x) > 170) continue;  //总和n无法到达
                ll &v = dp[i - 1][j][sum - x * (k - x)];//被更新状态
                if (v < 0) v = 0;
                v = (v + u * C(k - j, x - j)) % mod;
            }
        }
        else //当前上界为1
        {
            rep(j2, 0, j) rep(x, 0, k - j)
            {
                if ((j2 + x) * (k - j2 - x) > sum) continue;            //总和n被超过
                if (sum - (j2 + x) * (k - j2 - x) > 170) continue;      //总和n无法到达
                ll &v = dp[i - 1][j2][sum - (j2 + x) * (k - j2 - x)];   //被更新状态
                if (v < 0) v = 0;
                v = (v + u * C(j, j2) * C(k - j, x)) % mod;
            }
        }
    }
    ll ans(0);
    rep(i, 0, k) ans = (ans + (dp[0][i][0] > 0 ? dp[0][i][0] : 0)) % mod;
    cout << ans << endl;
    return 0;
}

dfs写法

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;

ll n, m, k;

const int mod = 1e9 + 7;
const int FN = 25;
ll fac[FN];//阶乘数组
ll ifc[FN];//阶乘逆元
ll inv[FN];//逆元

void init(int n)
{
    fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
    rep(i, 2, n)
    {
        fac[i] = fac[i - 1] * i % mod;
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
        ifc[i] = ifc[i - 1] * inv[i] % mod;
    }
}

ll C(ll n, ll m)
{
    if (n < m) return 0;
    return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}

ll dp[45][20][175];
int lim[45];

ll dfs(int w, int num, int sum)
{
    if (sum < 0 || sum > 170) return 0;
    if (w < 0) return sum ? 0 : 1;
    if (~dp[w][num][sum]) return dp[w][num][sum];
    ll &u = dp[w][num][sum]; u = 0;
    int need = sum * 2 + ((n >> w) & 1);
    if (lim[w])
    {
        rep(i, 0, num) rep(j, 0, k - num)
        {
            int x = (i + j) * (k - i - j);
            u = (u + dfs(w - 1, i, need - x) * C(num, i) * C(k - num, j)) % mod;
        }
    }
    else
    {
        rep(i, num, k)
        {
            int x = i * (k - i);
            u = (u + dfs(w - 1, num, need - x) * C(k - num, i - num)) % mod;
        }
    }
    return u;
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m >> k;
    init(22);
    rep(i, 0, 40) lim[i] = (m >> i) & 1;
    memset(dp, -1, sizeof(dp));
    cout << dfs(40, k, n >> 41) << endl;
    return 0;
}

J Math Exam

知识点: 折线模型，容斥

在看完题解后，学长扔过来一道题，说是原题....P3266 [JLOI2015]骗我呢

emmmmmm,怎么说呢，看完题解后，我满脑子都是: 这是人能想到的？

先看这题题面

[JLOI2015]骗我呢

题目描述

说起来，毕业之后 B 君也就见过 R 君两面而已。

R 君有一个 \(n \times m\) 的数组 \(x_{i,j}(1 \le i \le n; 1 \le j \le m)\)。

对于 \(1 \le i \le n; 1 \le j \le m\)，满足\(0 \le x_{i,j} \le m\)。求 可能的数组\(x_{i,j}\) 的解数。

B 君觉得限制太宽松，还要求对于 \(1 \le i \le n; 1 \le j<m\)，满足 \(x_{i,j} <x_{i,j+1}\)，对于\(1 <i \le n; 1 \le j<m\)，满足 \(x_{i,j} <x_{i-1,j+1}\)。

B 君认为 R 君可以直接 pwn 掉这个题。

R 君说：「黑的实在逼真 =.=，你起码把解数模 \(10^9+7\) 吧。」B 君觉得 R 君说的有道理，于是想让你求解数模 \(10^9+7\) 的结果。

输入格式

一行两个整数表示 \(n, m\)，含义如题目中所述。

输出格式

一行一个数表示同时满足 B 君和 R 君的条件 \(x_{i,j}\) 的解数，模 \(10^9+7\) 的结果。

样例 #1

样例输入 #1

3 3

样例输出 #1

40

提示

对于 \(100\%\) 的数据，\(1 \leq m, n \leq 10^6\)

我的水平只能支持我看懂dp和dp的简化

至于后面的模型转换，真的看了我几个小时

第一篇题解和第二篇题解在最后计算答案时开始变的无比抽象

比如我一开始完全没懂第一篇的字符串ABABA....是在干什么

第二篇计算答案这里的\(C_{2n+m+1}^{n}-C_{2n+m+1}^{n+m+2}-C_{2n+m+1}^{n-1}\)就完全不知道在说什么

其实就是没完全理解折线模型，或者说基本没做过相关题目，总结：就是菜

在看到这篇题解的时候才明白，原来是终点关于两条直线的对称点

明白这一点后，后面的容斥就十分自然，真的自然吗QAQ

这篇题解开头说的真的说到我心坎上了：

我人傻了啊……想了一两个小时，想出了个屁……这是什么东西哦……真的离天下之大谱！

理解完思路后，代码反而变得十分好写

---

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)

const int mod = 1e9 + 7;

namespace cnm
{
    const int FN = 3e6 + 5;
    ll fac[FN];//阶乘数组
    ll ifc[FN];//阶乘逆元
    ll inv[FN];//逆元

    void init(int n)
    {
        fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
        rep(i, 2, n)
        {
            fac[i] = fac[i - 1] * i % mod;
            inv[i] = (mod - mod / i) * inv[mod % i] % mod;
            ifc[i] = ifc[i - 1] * inv[i] % mod;
        }
    }
    ll C(ll n, ll m)
    {
        if (n < m) return 0;
        return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
    }
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;

int n, m;

ll A(ll x, ll y);
ll B(ll x, ll y);

ll A(ll x, ll y)
{
    if (x < 0 || y < 0) return 0;
    return (C(x + y, x) - B(y + 1, x - 1) + mod) % mod;
}

ll B(ll x, ll y)
{
    if (x < 0 || y < 0) return 0;
    return (C(x + y, x) - A(y - m - 2, x + m + 2) + mod) % mod;
}

int main()
{
    cin >> n >> m;
    cnm::init(n * 2 + m + 1);
    ll ans = C(n * 2 + m + 1, n);
    ans = (ans - A(n - 1, n + m + 2) + mod) % mod;
    ans = (ans - B(n + m + 2, n - 1) + mod) % mod;
    cout << ans << endl;
    return 0;
}

---

在解决完学长扔出的题目后，开始尝试解决该题

显然我们能通过\(4S_i = a_i^2 + 2a_i+1\)化简得到

\[a_i=\begin{cases}
-a_{i-1}\\
a_{i-1} + 2
\end{cases}
\]

看完题解后，我们就有了第一步的模型转换

\[b[i] = \frac{|a[i]+1|}{2}
\]

我的理解是：

• 绝对值为了处理\(a_i=-a_{i-1}\)
• 除2是为了让步长为1
• +1可能是为了变成折线模型

此时模型变成了 \(b_i\) 从 \((0,0)\) 出发，每次可以向右上或右下走

但是不能碰到直线 \(y = - 1\) 与 \(y = \frac{m+1}{2} + 1\)

为了变成折线模型，我们重新处理坐标系

将模型转换成 \(b_i\) 从 \((0,0)\) 出发，每次可以向上或者右走

但是不能碰到直线 \(y = x - 1\) 与 \(y = x + \frac{m+1}{2} + 1\)

此时模型就与上一题相似了

当 \(n=5\)，\(m=3\) 时如图

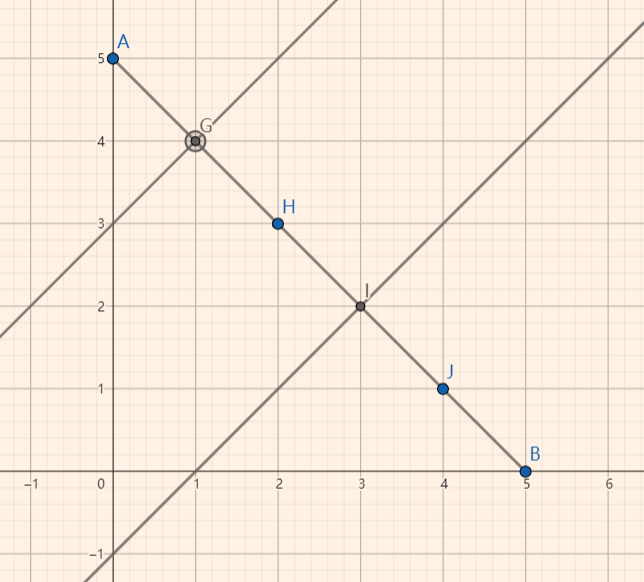
显然对于 A,G,H,I,J,B 就只有 H 有 \(C_5^2\) 种情况(包括不合法的情况)

然后对于碰到直线 \(y = x + 3\) 与 \(y = x - 1\) 的情况我们就需要进行容斥去除不合法的路线

于是我就写下了如下代码

---

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
template<class T> using vc = vector<T>;

const int mod = 998244353;

namespace cnm
{
    const int FN = 1e7 + 5;
    int fac[FN];//阶乘数组
    int ifc[FN];//阶乘逆元
    int inv[FN];//逆元

    void init(int n)
    {
        fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
        rep(i, 2, n)
        {
            fac[i] = (ll)fac[i - 1] * i % mod;
            inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;
            ifc[i] = (ll)ifc[i - 1] * inv[i] % mod;
        }
    }
    ll C(ll n, ll m)
    {
        if (n < m || m < 0) return 0;
        return (ll)fac[n] * ifc[m] % mod * ifc[n - m] % mod;
    }
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;

ll ksm(ll x, ll n)
{
    ll ret = 1;
    while (n)
    {
        if (n & 1) ret = ret * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return ret;
}

int n, m;

int main()
{
    cin >> n >> m;
    cnm::init(n);
    vc<int> pre(n + 2, 0);
    rep(i, 0, n) pre[i + 1] = ((ll)pre[i] + C(n, i)) % mod;
    auto sum = [&](int l, int r) -> ll
    {
        l = max(l, 0);
        r = min(r, n);
        if (l > r) return 0;
        return ((ll)pre[r + 1] - pre[l] + mod) % mod;
    };
    m = (m + 1) / 2;
    ll l = (n - m + 1) / 2, r = n / 2;
    ll ans = sum(l, r);
    function<ll(int, int)> A, B;
    A = [&](int l, int r) -> ll
    {
        l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
        if (l > n || r < 0) return 0;
        return (sum(l, r) - B(l, r) + mod) % mod;
    };
    B = [&](int l, int r) -> ll
    {
        l = n - l + 1, r = n - r + 1; swap(l, r);
        if (l > n || r < 0) return 0;
        return (sum(l, r) - A(l, r) + mod) % mod;
    };
    ans = (ans - A(l, r) + mod) % mod;
    ans = (ans - B(l, r) + mod) % mod;
    cout << ans << endl;
    return 0;
}

但是问题来了，爆空间了，还是在我把4个 longlong 数组改成 int 的情况下爆空间了，所以我认为是栈空间爆了

那么就必须换写法了，我绝对不会说我看的杜老师代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
template<class T> using vc = vector<T>;

const int mod = 998244353;

namespace cnm
{
    const int FN = 1e7 + 5;
    int fac[FN];//阶乘数组
    int ifc[FN];//阶乘逆元
    int inv[FN];//逆元

    void init(int n)
    {
        fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
        rep(i, 2, n)
        {
            fac[i] = (ll)fac[i - 1] * i % mod;
            inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;
            ifc[i] = (ll)ifc[i - 1] * inv[i] % mod;
        }
    }
    ll C(ll n, ll m)
    {
        if (n < m || m < 0) return 0;
        return (ll)fac[n] * ifc[m] % mod * ifc[n - m] % mod;
    }
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;

ll ksm(ll x, ll n)
{
    ll ret = 1;
    while (n)
    {
        if (n & 1) ret = ret * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return ret;
}

int n, m;

int main()
{
    cin >> n >> m;
    cnm::init(n);
    vc<int> pre(n + 2, 0);
    rep(i, 0, n) pre[i + 1] = ((ll)pre[i] + C(n, i)) % mod;
    auto sum = [&](int l, int r) -> ll
    {
        l = max(l, 0);
        r = min(r, n);
        if (l > r) return 0;
        return ((ll)pre[r + 1] - pre[l] + mod) % mod;
    };
    m = (m + 1) / 2;
    ll l = (n - m + 1) / 2, r = n / 2;
    ll ans = sum(l, r);
    while (true)
    {
        l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
        ans = (ans - sum(l, r) + mod) % mod;
        l = n - l + 1, r = n - r + 1; swap(l, r);
        ans = (ans + sum(l, r)) % mod;
        if (l > n || r < 0) break;
    }
    l = (n - m + 1) / 2, r = n / 2;
    while (true)
    {
        l = n - l + 1, r = n - r + 1; swap(l, r);
        ans = (ans - sum(l, r) + mod) % mod;
        l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
        ans = (ans + sum(l, r)) % mod;
        if (l > n || r < 0) break;
    }
    cout << ans << endl;
    return 0;
}

---

1. 当起始感染点被确定后，其它点被感染只有当其父亲被感染时才会被感染 ︎

2. 也可能只是我菜，写的题太少没见过 ︎