DFS算法-求集合的所有子集

目录

• 1. 题目来源
• 2. 普通方法
  • 1. 思路
  • 2. 代码
  • 3. 运行结果
• 3. DFS算法
  • 1. 概念
  • 2. 解题思路
  • 3. 代码
  • 4. 运行结果
• 4. 对比

---

1. 题目来源

牛客网，集合的所有子集(一)

https://www.nowcoder.com/practice/c333d551eb6243e0b4d92e37a06fbfc9

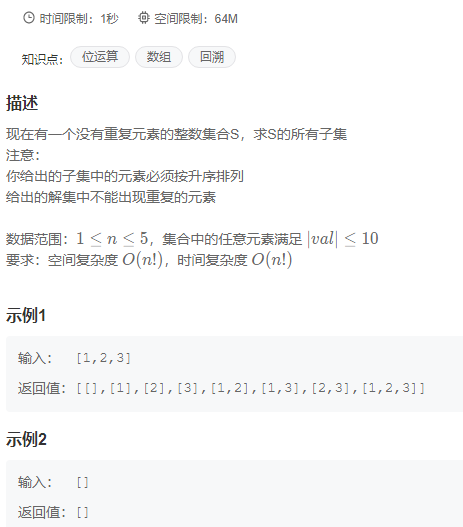
2. 普通方法

1. 思路

数学上排列组合中的组合，从N个元素的集合中拿出M(0≤ M ≤ N)个元素的可能数，标记为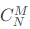

。M从0开始遍历到N，就是所求的所有子集合。这里要结果不是数，而且取的元素集合。

这里具体在做的就是用遍历索引的方式取出想要的集合

• 比如数组为{1, 2, 3, 4, 5}，要取0个数，那么所有可能就是{}。1个集合
• 比如数组为{1, 2, 3, 4, 5}，要取1个数，那么所有可能就是{{1}, {2}, {3}, {4}, {5}}。5个集合
• 比如数组为{1, 2, 3, 4, 5}，要取2个数，那么所有可能就是{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}}。10个集合
• 比如数组为{1, 2, 3, 4, 5}，要取3个数，那么所有可能就是{{1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}}。10个集合
• 比如数组为{1, 2, 3, 4, 5}，要取4个数，那么所有可能就是{{1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 4, 5}, {1, 3, 4, 5}, {2, 3, 4, 5}}。5个集合
• 比如数组为{1, 2, 3, 4, 5}，要取5个数，那么所有可能就是{{1, 2, 3, 4, 5}}。1个集合

2. 代码

import java.util.ArrayList;

/**
 * @className SolutionTest
 * @description
 * @author liwei
 * @date 2022/9/8 15:29
 * @version V1.0
 **/
public class SolutionTest {

    public static void main(String[] args) {
        int[] ints = {5, 4, 3, 2, 1};
        System.out.println(subsets(ints));
    }

    public static ArrayList<ArrayList<Integer>> subsets(int[] ints) {
        // 插入排序，升序排列
        for (int i = 0, length = ints.length; i < length - 1; i++) {
            int tmpValue = ints[i];
            int tmpIndex = i;
            for (int j = i + 1; j < ints.length; j++) {
                if (tmpValue > ints[j]) {
                    tmpValue = ints[j];
                    tmpIndex = j;
                }
            }
            if (i != tmpIndex) {
                ints[tmpIndex] = ints[i];
                ints[i] = tmpValue;
            }
        }

        ArrayList<ArrayList<Integer>> lists = new ArrayList<>();

        // 循环，需要从数组中取i个数，然后取出i个数的所有可能。
        // 比如数组为{1, 2, 3, 4, 5}，要取1个数，那么所有可能就是{{1}, {2}, {3}, {4}, {5}}
        // 比如数组为{1, 2, 3, 4, 5}，要取2个数，那么所有可能就是{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}}
        for (int number = 0; number <= ints.length; number++) {
            lists.addAll(subsets(ints, number));
        }

        return lists;
    }

    /**
     * 取多少个元素的子集集合
     *
     * @param ints
     *        数组
     * @param number
     *        要取的元素个数
     * @return java.util.ArrayList<java.util.ArrayList < java.lang.Integer>>
     * @author liwei
     * @date 2022/8/10 20:22
     */
    public static ArrayList<ArrayList<Integer>> subsets(int[] ints, int number) {
        ArrayList<ArrayList<Integer>> lists = new ArrayList<>();
        // 特殊处理，如果需要的个数为0，那么直接添加一个空集合，然后返回
        if (number <= 0) {
            lists.add(new ArrayList<>());
            return lists;
        }
        int length = ints.length;

        // 特殊处理，如果需要的个数大于等于数组元素个数，那么直接添加一个所有元素的集合，然后返回
        if (length <= number) {
            ArrayList<Integer> arrayList = new ArrayList<>();
            for (int i1 : ints) {
                arrayList.add(i1);
            }
            lists.add(arrayList);
            return lists;
        }

        // 用于存储取数组元素的下标。例如数组为[6,7,8,9]，要取2个数，那么这里的indexs数组长度就为2，下面初始化索引为最开始索引，indexs=[0,1]
        int[] indexs = new int[number];
        // 初始化索引
        for (int j = 0; j < number; j++) {
            indexs[j] = j;
        }

        // 循环，索引数组的第一个值索引+个数>数组个数，就跳出循环
        while (indexs[0] + number <= length) {
            // 最后一个索引循环，比如最初indexs=[0,1]，数组元素个数为4，那么这里循环，indexs=[0,1]、indexs=[0,2]、indexs=[0,3]，跳出循环indexs=[0,4]
            for (int k = indexs[number - 1]; k < length; k++) {
                ArrayList<Integer> arrayList = new ArrayList<>();
                // 通过下标取数组中元素
                for (int index : indexs) {
                    arrayList.add(ints[index]);
                }
                lists.add(arrayList);
                // 最后一个索引往后移动
                indexs[number - 1]++;
            }

            // 上面索引数组中最后一个值已经到了最后，这里是把倒数第二个值+1，如果倒数第二也到了最后，那么再往前找，直到第一个。
            // 1、例如数组为[5,6,7,8,9]，要取得元素个数为3，索引数组初始化为indexs=[0,1,2]，经过上面最后一个索引循环变成indexs=[0,1,5]，这里循环得作用就是把索引数组变成indexs=[0,2,3]
            // 2、如果经过上面最后一个索引循环变成indexs=[0,4,5]，这里循环得作用就是把索引数组变成indexs=[1,2,3]
            for (int l = number - 2; l >= 0; l--) {
                // 索引数组只修改一次就跳出循环
                if (indexs[l] < indexs[l + 1] - 1) {
                    indexs[l]++;
                    for (int m = l + 1; m < number; m++) {
                        indexs[m] = indexs[m - 1] + 1;
                    }
                    break;
                }
            }
        }
        return lists;
    }
}

3. 运行结果

[[], [1], [2], [3], [4], [5], [1, 2], [1, 3], [1, 4], [1, 5], [2, 3], [2, 4], [2, 5], [3, 4], [3, 5], [4, 5], [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5], [1, 2, 3, 4], [1, 2, 3, 5], [1, 2, 4, 5], [1, 3, 4, 5], [2, 3, 4, 5], [1, 2, 3, 4, 5]]

3. DFS算法

Depth-First Search深度优先搜索算法

1. 概念

在深度优先搜索中，对于最新发现的顶点，如果它还有以此为顶点而未探测到的边，就沿此边继续探测下去，当顶点v的所有边都已被探寻过后，搜索将回溯到发现顶点v有起始点的那些边。

这一过程一直进行到已发现从源顶点可达的所有顶点为止。如果还存在未被发现的顶点，则选择其中一个作为源顶点，并重复上述过程。

整个过程反复进行，直到所有的顶点都被发现时为止。

比如数组{1,2,3,4,5}所有子集合，这里不包括空集合

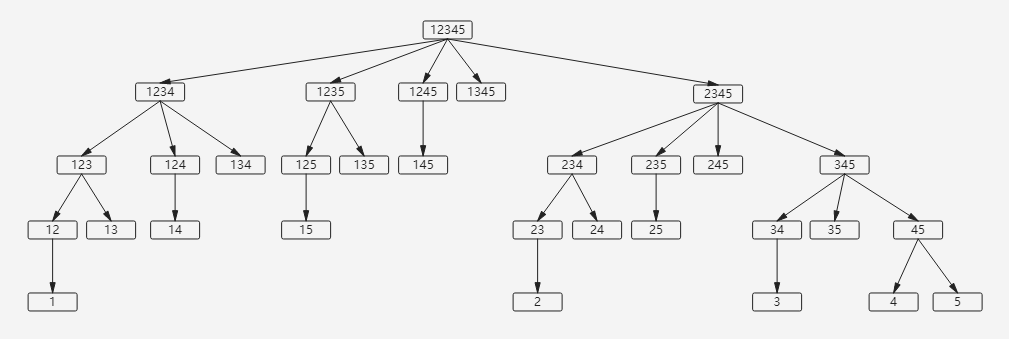
2. 解题思路

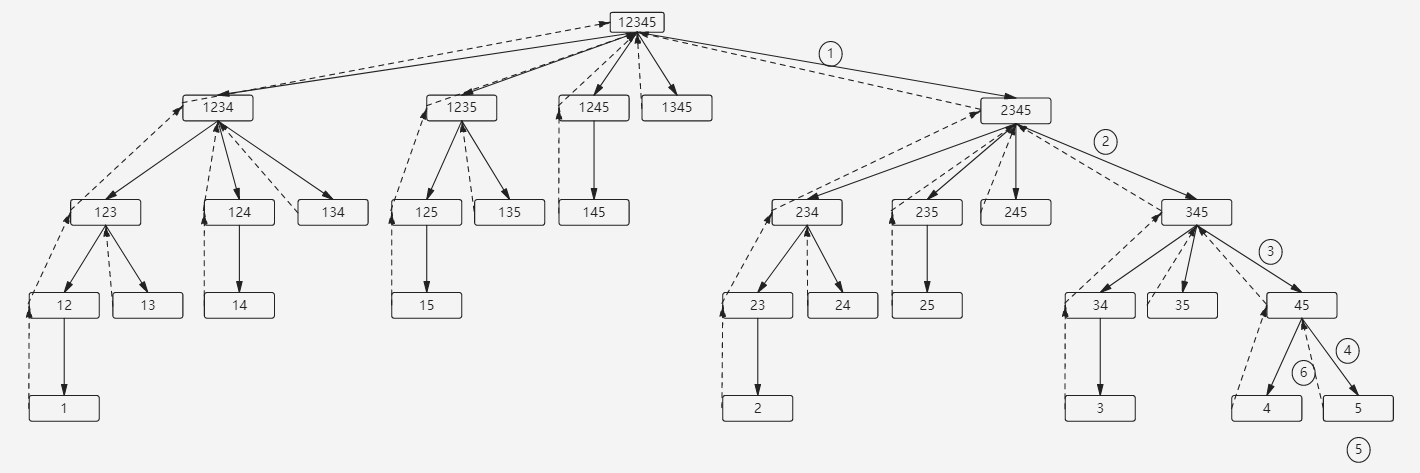
如下图，探索和回溯，探索是实线箭头表示，回溯是虚线箭头表示。其中虚线箭头指向中间表示这个节点还有其他子节点没有探索完，虚线箭头指向右边便是这个节点已经探索完成。

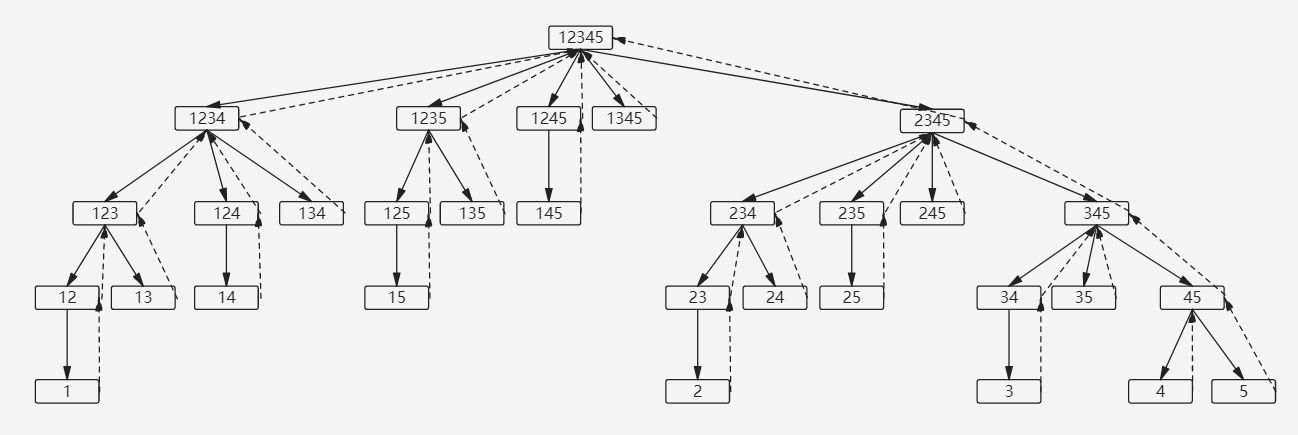
在这里我们从最右开始，就会发现里面的递归。数组{1,2,3,4,5}的所有子集合划分为几部分：

1. 含有元素1的所有集合。【发现在下面第2、3、4、5基础上加上空集合，然后每个集合都加上元素1，就是此时要求的所有集合】

【{1}, {1, 2}, {1, 2, 3}, {1, 2, 3, 4}, {1, 2, 3, 4, 5}, {1, 2, 3, 5}, {1, 2, 4}, {1, 2, 4, 5}, {1, 2, 5}, {1, 3}, {1, 3, 4}, {1, 3, 4, 5}, {1, 3, 5}, {1, 4}, {1, 4, 5}, {1, 5}】，16个集合

1. 含有元素2且不包含元素1的所有集合。【发现在下面第3、4、5基础上加上空集合，然后每个集合都加上元素2，就是此时要求的所有集合】

【{2}, {2, 3}, {2, 3, 4}, {2, 3, 4, 5}, {2, 3, 5}, {2, 4}, {2, 4, 5}, {2, 5}】，8个集合

1. 含有元素3且不包含元素1和元素2的所有集合。【发现在下面第4、5基础上加上空集合，然后每个集合都加上元素3，就是此时要求的所有集合】

【{3}, {3, 4}, {3, 4, 5}, {3, 5}】，4个集合

1. 含有元素4且不包含元素1、元素2和元素3的所有集合。【发现在下面第5基础上加上空集合，然后每个集合都加上元素4，就是此时要求的所有集合】

【{4}, {4, 5}】，2个集合

1. 含有元素5且不包含元素1、元素2、元素3和元素4的所有集合。【此时只有一个元素5，那么就只有一个集合，集合里面就一个元素5】

【{5}】，1个集合

3. 代码

import java.util.ArrayList;

/**
 * @className FDSTest
 * @description FDS算法在求集合的所有子集合，包括空集合时的应用
 * @author liwei
 * @date 2022/9/8 15:29
 * @version V1.0
 **/
public class FDSTest {

    public static void main(String[] args) {
        int[] ints = {5, 4, 3, 2, 1};
        System.out.println(subsets(ints));
    }

    /**
     * @description 求数组的所有子集合，包括空数组。按要求升序排序数组
     * @author liwei
     * @date 2022/9/9 11:45
     * @param ints
     *        数组
     * @return java.util.ArrayList<java.util.ArrayList<java.lang.Integer>>
     **/
    public static ArrayList<ArrayList<Integer>> subsets(int[] ints) {
        // 插入排序，升序排列
        for (int i = 0, length = ints.length; i < length - 1; i++) {
            int tmpValue = ints[i];
            int tmpIndex = i;
            for (int j = i + 1; j < ints.length; j++) {
                if (tmpValue > ints[j]) {
                    tmpValue = ints[j];
                    tmpIndex = j;
                }
            }
            if (i != tmpIndex) {
                ints[tmpIndex] = ints[i];
                ints[i] = tmpValue;
            }
        }

        // 调用FDS
        return subsetsFDS(ints);
    }

    /**
     * @description FDS算法求解数组的所有子集合，包括空数组，内含递归
     * @author liwei
     * @date 2022/9/9 11:47
     * @param ints
     *        数组
     * @return java.util.ArrayList<java.util.ArrayList<java.lang.Integer>>
     **/
    public static ArrayList<ArrayList<Integer>> subsetsFDS(int[] ints) {
        ArrayList<ArrayList<Integer>> arrayList = new ArrayList<>();
        if (null == ints || ints.length <= 0) {
            // 递归到最后没有元素的话返回空集合
            arrayList.add(new ArrayList<>());
            return arrayList;
        }

        // 取第一个元素
        int one = ints[0];
        // 定义取完第一个元素后剩余数组长度
        int[] twoArray = new int[ints.length - 1];

        for (int i = 1; i < ints.length; i++) {
            twoArray[i - 1] = ints[i];
        }

        // 递归，取出第一个元素后，递归得到不包含第一个元素的所有子集合
        ArrayList<ArrayList<Integer>> listArrayList = subsetsFDS(twoArray);
        for (ArrayList<Integer> integers : listArrayList) {
            // 把集合复制一份保存到返回集合中
            arrayList.add(new ArrayList<>(integers));

            // 在集合第一位置添加第一个元素，然后保存到返回集合中
            integers.add(0, one);
            arrayList.add(integers);
        }

        return arrayList;
    }
}

4. 运行结果

[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3], [4], [1, 4], [2, 4], [1, 2, 4], [3, 4], [1, 3, 4], [2, 3, 4], [1, 2, 3, 4], [5], [1, 5], [2, 5], [1, 2, 5], [3, 5], [1, 3, 5], [2, 3, 5], [1, 2, 3, 5], [4, 5], [1, 4, 5], [2, 4, 5], [1, 2, 4, 5], [3, 4, 5], [1, 3, 4, 5], [2, 3, 4, 5], [1, 2, 3, 4, 5]]

4. 对比

1. 普通方法的优势：如果是指定取M个数，如上面例子我们只取出只有2个元素的所有集合；
2. DFS算法的优势：这里只是这个算法的一种体现，最重要的是算法思想。例如求2点间最短距离；