仿射变换(Affine Transformation)
转自:https://www.cnblogs.com/bnuvincent/p/6691189.html
http://www.cnblogs.com/ghj1976/p/5199086.html
变换模型是指根据待匹配图像与背景图像之间几何畸变的情况,所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种:刚性变换、仿射变换、透视变换和非线形变换等,如下图:

参考: http://wenku.baidu.com/view/826a796027d3240c8447ef20.html
其中第三个的仿射变换就是我们这节要讨论的。
仿射变换(Affine Transformation)
Affine Transformation是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(译注:straightness,即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(译注:parallelness,其实是指保二维图形间的相对位置关系不变,平行线还是平行线,相交直线的交角不变。)。

c和d的区别可以看下图:

仿射变换可以通过一系列的原子变换的复合来实现,包括:平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)。

仿射变换可以用下面公式表示:

参考:http://wenku.baidu.com/view/826a796027d3240c8447ef20.html
这个矩阵乘法的计算如下:
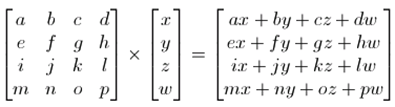
具体到二维的仿射变换的计算如下:

几种典型的仿射变换如下:
平移变换 Translation
将每一点移动到(x+tx, y+ty),变换矩阵为: 
平移变换是一种“刚体变换”,rigid-body transformation,就是不会产生形变的理想物体。
效果:
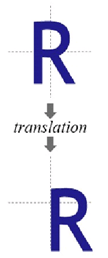
缩放变换(Scale)
将每一点的横坐标放大(缩小)至sx倍,纵坐标放大(缩小)至sy倍,变换矩阵为:

变换效果如下:

剪切变换(Shear)
变换矩阵为:

相当于一个横向剪切与一个纵向剪切的复合
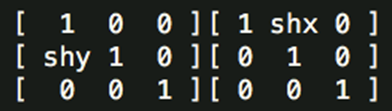
效果:
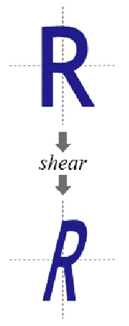
旋转变换(Rotation)
目标图形围绕原点顺时针旋转theta弧度,变换矩阵为:

效果:

组合
旋转变换,目标图形以(x, y)为轴心顺时针旋转theta弧度,变换矩阵为:

相当于两次平移变换与一次原点旋转变换的复合:

先移动到中心节点,然后旋转,然后再移动回去。
这个转换矩阵也可以下面这样描述。 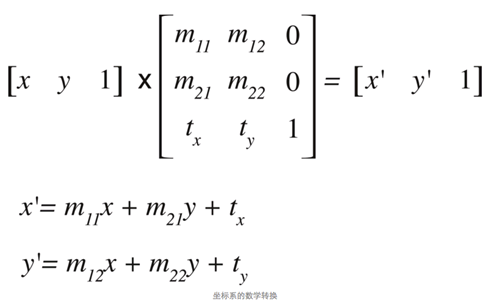
一些常用转换矩阵如下:
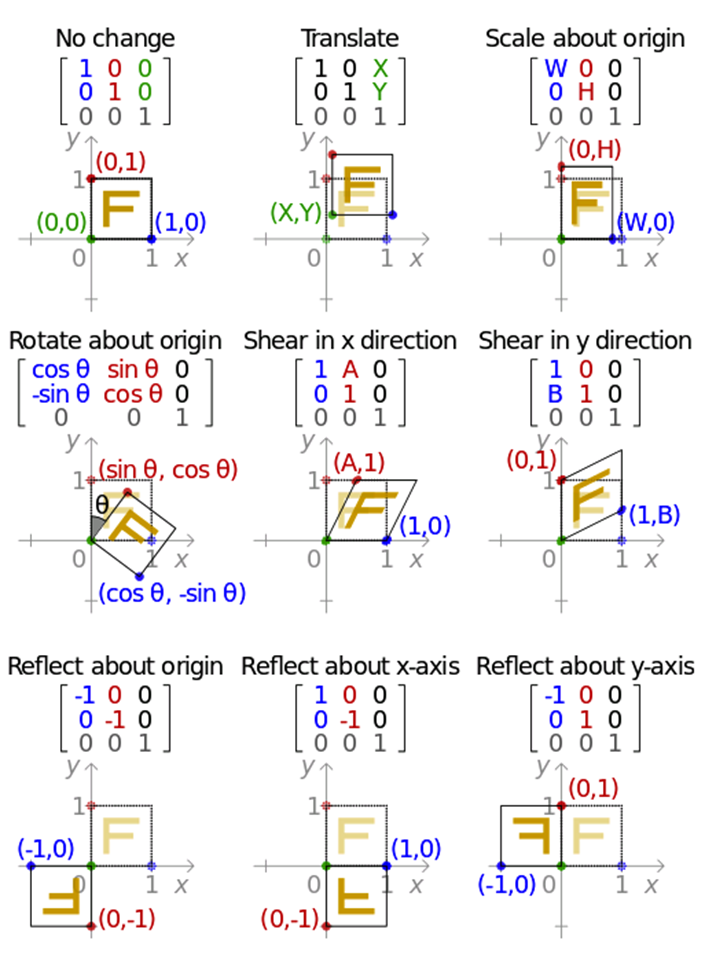
仿射变换(Affine Transformation)的更多相关文章
- 何为仿射变换(Affine Transformation)
http://www.cnblogs.com/ghj1976/p/5199086.html 变换模型是指根据待匹配图像与背景图像之间几何畸变的情况,所选择的能最佳拟合两幅图像之间变化的几何变换模型.可 ...
- affine transformation matrix 仿射变换矩阵 与 OpenGL
变换模型是指根据待匹配图像与背景图像之间几何畸变的情况,所选择的能最佳拟合两幅图像之间变化的几何变换模型.可采用的变换模型有如下几种:刚性变换.仿射变换.透视变换和非线形变换等,如下图: 参考: ht ...
- QANet
Reading Comprehension(RC) 阅读理解对于机器来说, 是一项非常艰巨的任务.google提出QANet, 目前(2018 0505)一直是SQuAD的No. 1. 今天简单地与大 ...
- 【Computer Vision】图像单应性变换/投影/仿射/透视
一.基础概念 1. projective transformation = homography = collineation. 2. 齐次坐标:使用N+1维坐标来表示N维坐标,例如在2D笛卡尔坐标 ...
- Capsule Network
Capsule Network最大的特色在于vector in vector out & 动态路由算法. vector in vector out 所谓vector in vector out ...
- 写给程序员的机器学习入门 (十) - 对象识别 Faster-RCNN - 识别人脸位置与是否戴口罩
每次看到大数据人脸识别抓逃犯的新闻我都会感叹技术发展的太快了,国家治安水平也越来越好了
- 通过Matrix进行二维图形仿射变换
Affine Transformation是一种二维坐标到二维坐标之间的线性变换,保持二维图形的"平直性"和"平行性".仿射变换可以通过一系列的原子变换的复合来 ...
- 【OpenCV新手教程之十八】OpenCV仿射变换 & SURF特征点描写叙述合辑
本系列文章由@浅墨_毛星云 出品,转载请注明出处. 文章链接:http://blog.csdn.net/poem_qianmo/article/details/33320997 作者:毛星云(浅墨) ...
- opencv 之 transformation
getAffineTransform() : calculates an affine transform from three pairs of the corresponding points. ...
随机推荐
- Xcode10适配——Error:Multiple commands produce
今天苹果正式推送了iOS12,今天上午就更新了最新的iOS,及Xcode10.这次更新还行,不需要我们对以前的项目紧急修复,大动手术. 用Xcode10跑之前的项目,也就报了一种类型的错误:Multi ...
- 有效解决ajax传中文时,乱码的情况,php处理接收到的值
在抽奖环节时,需把获奖名单通过ajax的post方式传输给php后台进行储存,但是php接收到的值确是乱码.在百度之后并没有找到合适的解决方法. 则使用js的encodeURI函数可以有效解决,但不知 ...
- HDU 1005 Number Sequence(找规律)
链接:传送门 题意:略 思路:f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7 -> f(n) = (A * f(n-1)%7 + B * f(n-1)%7) ...
- 洛谷P1004 方格取数
网络流大法吼 不想用DP的我选择了用网络流-- 建模方法: 从源点向(1,1)连一条容量为2(走两次),费用为0的边 从(n,n)向汇点连一条容量为2,费用为0的边 每个方格向右边和下边的方格连一条容 ...
- Vue-router入门
1.npm install vue-router --save-dev 安装路由包,在安装脚手架时实际上可以直接安装 2.解读核心文件 router/index.js文件 import Vue fro ...
- ASP.NET-使用json
数据格式 vat strJson =' {"name":"jingya","Age":88} '; // 数字不用写双引号 JSON.par ...
- 洛谷 P2243 电路维修
P2243 电路维修 题目背景 Elf 是来自Gliese 星球的少女,由于偶然的原因漂流到了地球上.在她无依无靠的时候,善良的运输队员Mark 和James 收留了她.Elf 很感谢Mark和Jam ...
- Android中通过ViewHelper.setTranslationY实现View移动控制(NineOldAndroids开源项目)
我们知道有不少开源project,能实现非常多不错的效果.前几天,我看了一个效果,刚好项目中也用到了这个jar包. 没事挖一挖 学一学(一说到挖一挖.那么问题来了.挖掘机技术究竟哪家强 ),看看不错的 ...
- python-Pymyslql-requests_html:把腾讯新闻的今日推荐和链接存进数据库
使用pumsql封装的部分功能 request_html:打开www.qq.com的例子 结果: PS:记得处理数据
- JAVA网络编程--UDP通信
首先网络传输数据需了解例如以下三点 1.找到对方IP 2.数据要发送到对方指定的应用程序上,为了标识这些应用程序,所以给这些网络应用程序用数字进行了标识.为了方便称呼这个数字,叫做port,逻辑por ...
