[arc082e]ConvexScore

题意：

给出直角坐标系中的$N$个点$(X_i,Y_i)$，定义由其中部分点构成的点集为“凸点集”当且仅当这些点恰好能构成一个凸多边形（内部没有其他点）。

如图，点集$\{A,C,E\}$和$\{B,D,E\}$是凸点集，而$\{A,C,D,E\}$,$\{A,B,C,E\}$,$\{A,B,C\}$,$\{D,E\}$和$∅$则不是。

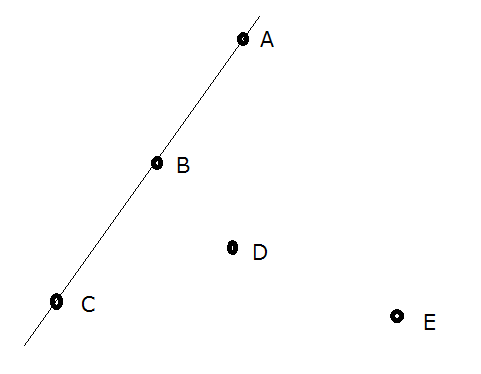
对于每个凸点集$S$，设这个凸点集内部（包括内部的点，所有顶点和边上的点）一共有$m$个点，那么它对答案的贡献就是$2^{m-|S|}$，求答案模998244353的结果。

$1\leq N\leq 200$

题解：

这题题面看起来很可怕。。。开始以为要写凸包的东西，看到那个998244353又以为是多项式相关。。。但是实际上这个模数是吓人的。。。理解了题意就非常好做了。

考虑一个凸点集$S$，设它内部的所有点组成的集合为$A$，显然$|A|=m$。那么有$2^{m-|S|}=2^{|A|-|S|}$。观察$|A|-|S|$这个式子，实际上表示的就是$S$内部不包括边界上的点的个数，即$|\complement_{A}S|$。那么$2^{m-|S|}$的实际意义就是$\complement_{A}S$的子集个数。至此题意就转化为在$\complement_{A}S$里随便选点，选出来之后再加上$S$，方案总数便是对答案的贡献。这些选点方案的共同点就是边界$S$是一样的，而凸点集内部的情况不同，换一种说法，就是这些点所能形成的凸包都是相同的。考虑原问题点集中的任意一个凸包，它对答案的贡献就是内部的点集的子集个数。然后我们惊奇的发现：这求的就是能形成凸包的点集个数！进一步，就是原点集中凸包的个数！

那么可以直接暴力。。。考虑不能形成凸包的情况，就是三个或以上的点共线，设有$(n+2)$个点共线，那么答案就会少$2^n$。原本点集中点数大于等于3的点集个数是$2^{n}-1-n-\binom{n}{2}$，再减去上面共线的情况减少的就行了。。。

$O(n^3)$搞定

代码：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #define mod 998244353
 using namespace std;
 typedef long long ll;
 int n,ans,x[],y[],pw[];
 int main(){
     scanf("%d",&n);
     pw[]=;
     for(int i=;i<=n;i++)pw[i]=(ll)pw[i-]*%mod;
     for(int i=;i<=n;i++)scanf("%d%d",&x[i],&y[i]);
     ans=(pw[n]-n--n*(n-)/+mod)%mod;
     for(int i=;i<=n;i++){
         for(int j=i+;j<=n;j++){
             int tmp=;
             for(int k=j+;k<=n;k++){
                 if((y[j]-y[i])*(x[k]-x[j])==(y[k]-y[j])*(x[j]-x[i]))tmp++;
             }
             ans=(ans+mod+-pw[tmp])%mod;
         }
     }
     printf("%d",ans);
     return ;
 }

人家真的没有抄代码！口亨QAQ