Code VS 1002 搭桥

题目描述 Description

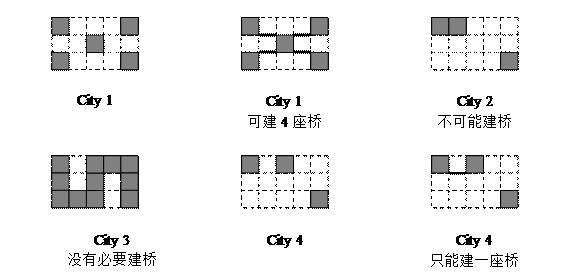
有一矩形区域的城市中建筑了若干建筑物，如果某两个单元格有一个点相联系，则它们属于同一座建筑物。现在想在这些建筑物之间搭建一些桥梁，其中桥梁只能沿着矩形的方格的边沿搭建，如下图城市1有5栋建筑物，可以搭建4座桥将建筑物联系起来。城市2有两座建筑物，但不能搭建桥梁将它们连接。城市3只有一座建筑物，城市4有3座建筑物，可以搭建一座桥梁联系两栋建筑物，但不能与第三座建筑物联系在一起。

输入描述 Input Description

在输入的数据中的第一行包含描述城市的两个整数r 和c, 分别代表从北到南、从东到西的城市大小(1 <= r <= 50 and 1 <=  c <= 50). 接下来的r 行, 每一行由c 个(“#”)和(“.”)组成的字符. 每一个字符表示一个单元格。“#”表示建筑物，“.”表示空地。

输出描述 Output Description

在输出的数据中有两行，第一行表示建筑物的数目。第二行输出桥的数目和所有桥的总长度。

样例输入 Sample Input

样例1

3 5

#...#

..#..

#...#

样例2

3 5

##...

.....

....#

样例3

3 5

#.###

#.#.#

###.#

样例4:

3 5

#.#..

.....

....#

样例输出 Sample Output

样例1

5

4 4

样例2

2

0 0

样例3

1

0 0

样例4

3

1 1

-----------------------------------------------------------------------------------------------------------------（分割线）

弄了几乎快2个半小时..............

主要是在建图上.......................

一开始居然连题目都看不懂.....

￥%&%#@……%&&%￥%......

 

思路：

这题，主要是dfs+最小生成树，算法是简单.....但建图不好建。

这题第一问很明显是求联通块的个数。

第二问是要求最小生成树，边及其长度总和。

因为联通块不是一个整体，所以需要做的事是求每个联通块间的最小距离。

这里说两种方法。

第一种，开四重循环，枚举点对，然后每次都更新联通块间的最小距离。

第二种，扫描法，枚举每一个城市点，然后以六个方向进行扫描（听着代码长度就不会少），然后每次扫描都更新某两联通块间的距离。

　　　　假设当前枚举的点是（x,y) , 则这六个方向为：  （x,i）,(x+1,i) (x-1,i) ,(y,i),(y+1,i),(y-1,i），每次扫描到和当前点的联通块编号不相等的点时就更新最小距离。

 

我用的是第二种，觉得第一种没挑战性...........

下面代码的g[i][j]表示联通块编号i与联通块编号为j的最小距离。

有问题留言。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 60
#define M 250900
using namespace std;

int G[N][N];                //图数组 

int en,n,r,c;            //边数，联通块个数，题目所描述的，r,c。 

struct edge{
    int s,e,d;
}ed[M];

bool operator < (const edge &a, const edge &b){            //重载运算符
    return a.d < b.d;
}

void add_edge(int s,int e,int d){                //建边
    en++;
    ed[en].s= s,ed[en].e =e ,ed[en].d = d;
}
int fa[M];

int getf(int now){                        //并查集
    if(now == fa[now])return now;
    else return fa[now] = getf(fa[now]);
}

void kruskal(){                        //kruskal算法
    sort(ed+,ed+en+);
    for(int a = ; a <= n; a++)fa[a] = a;
    int ans = ,num = ;
    for(int a = ; a <= en; a++){
        int f1 = getf(ed[a].s);
        int f2 = getf(ed[a].e);
        if(f1 != f2){
            fa[f1] = f2;
            ans += ed[a].d;
            num++;
        }
    }
    printf("%d %d\n",num,ans);
}

int tx[] = {,,,,-,-,,-};
int ty[] = {,-,,-,,-,,};

void dfs(int x,int y){                //求联通块
    G[x][y] = n;
    for(int i = ; i < ; i++){
        int xx = tx[i]+x;
        int yy = ty[i]+y;
        if(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] == -))
            dfs(xx,yy);
    }
}

int g[][];

void cread(int x,int y){            //将六个方向再细分，变成十二个方向（笑...）
    int xx,yy;
    xx = x+,yy = y+;;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-);
        yy++;
    }
    yy = y-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-);
        yy--;
    }
    xx = x,yy = y+;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-);
        yy++;
    }
    yy = y-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-);
        yy--;
    }
    xx = x-,yy = y+;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-);
        yy++;
    }
    yy = y-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-);
        yy--;
    }

    yy = y,xx = x+;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-);
        xx++;
    }
    xx = x-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-);
        xx--;
    }
    yy = y+,xx = x+;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-);
        xx++;
    }
    xx = x-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-);
        xx--;
    }
    yy = y-;xx = x+;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-);
        xx++;
    }
    xx = x-;
    while(xx >=  && xx <= r && yy >=  && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != )g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-);
        xx--;
    }
}

int main(){
    scanf("%d%d",&r,&c);
    for(int i = ; i <= r; i++){
        char s[];
        scanf("%s",s);
        for(int j = ; j < c; j++)
            if(s[j] == '#')G[i][j+] = -;
            else G[i][j+] = ;
    }
    for(int i = ; i <= r; i++){
        for(int j = ; j <= c; j++){
            if(G[i][j] == -){
                n++;
                dfs(i,j);
            }
        }
    }

    memset(g,0x3f,sizeof(g));

    printf("%d\n",n);
    for(int i = ; i <= r; i++)
      for(int j = ; j <= c; j++)
         if(G[i][j] != )cread(i,j);

    for(int i = ; i <= n; i++)
       for(int j = ; j <= n; j++)
          if(g[i][j] != g[][])add_edge(i,j,g[i][j]);
    kruskal();
    return ;
}