HDU 2256 Problem of Precision （矩阵快速幂）（推算）

Problem of Precision

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1375    Accepted Submission(s): 826

Problem Description

Input

The
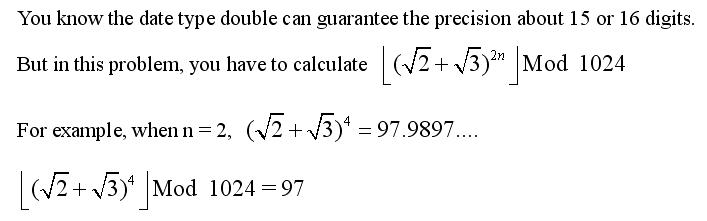
first line of input gives the number of cases, T. T test cases follow,
each on a separate line. Each test case contains one positive integer n.
(1 <= n <= 10^9)

Output

For each input case, you should output the answer in one line.

Sample Input

3
1
2
5

Sample Output

9 97 841

【分析】

这个题目算是矩阵快速幂的比较难推的一个题目。题目要求 （sqrt(2)+sqrt(3)）的 2^n并%1024，要求出值来并不难，构造矩阵即可，但是要mod1024就有问题了，小数不能直接mod，但是如果你取整之后再mod，结果绝逼出问题，因为浮点数的精度问题。

所以从斌牛的博客上看到如此推算，推算第一块不难，而且很容易求出Xn 和 Yn，但是问题又出来了，要是求出来后，直接用（int）（Xn+Yn*sqrt（6））%1024，又会出问题，还是浮点数取整问题，我一开始就这么算的，导致结果奇葩。看来在mod的时候有浮点数要格外注意，直接处理的话，不管怎么取整，都会出问题。

所以分割线下面的推算就避开了这个问题，这个确实好难想到，通过变换一下，得到最终的结果必定是2Xn-（0.101...）^n,因为最终mod是用不大于浮点数的最大整数在mod，所以最终结果就是2Xn-1.第二条确实好难想到！

题解转载于 http://www.cnblogs.com/kkrisen/p/3437710.html；

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <stack>
#include <queue>
#include <vector>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
using namespace std;
typedef long long ll;
const ll N = ;

ll f1,f2,k;
ll mod = ;
ll n;

struct Fast_Matrax {
    ll a[N][N];
    Fast_Matrax() {
        memset(a,,sizeof(a));
    }
    void init() {
        for(int i=; i<N; i++)
            for(int j=; j<N; j++)
                a[i][j]=(i==j);
    }
    Fast_Matrax operator * (const Fast_Matrax &B)const {
        Fast_Matrax C;
        for(int i=; i<N; i++)
            for(int k=; k<N; k++)
                for(int j=; j<N; j++)
                    C.a[i][j]=(C.a[i][j]+1LL*a[i][k]*B.a[k][j]%mod+mod)%mod;
        return C;
    }
    Fast_Matrax operator ^ (const ll &t)const {
        Fast_Matrax A=(*this),res;
        res.init();
        ll p=t;
        while(p) {
            if(p&)res=res*A;
            A=A*A;
            p>>=;
        }
        return res;
    }
} ans,tmp,x;
int main() {
    x.a[][]=;x.a[][]=;
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld",&n);
        if(n<=){
            puts("");
        }
        else {
            tmp.a[][]=;tmp.a[][]=;
            tmp.a[][]=;tmp.a[][]=;
            ans=(tmp^(n-))*x;
            printf("%lld\n",(*ans.a[][]-)%mod);
        }
    }
    return ;
}