matlab-罗曼诺夫斯基准则剔除粗大值
罗曼诺夫斯基准则原理
罗曼诺夫斯基准则又称 t检验准则,其特点是首先删除一个可疑的的测得值,然后按 t分布检验被剔除的测量值是否含有粗大误差
罗曼诺夫斯基准则
1)选取合适的显著度a,选择合适的数据处理长度n。由a、n在t分布表中查出系数K。(例如:a为0.05、n为15,则 K2.24)
2)计算处理段数据的平均值 3)计算处理段数据的标准 4)| 检测值 - 计算处理段数据的平均值 | > K*计算处理段数据的标准差,如果成立则检测值为粗大值,需要剔除。
实现代码
function out = fun_romanovsky(data, l, a)
% 功能:罗曼诺夫斯基准则剔除粗大值
% 参数:
% data 输入数据
% l 分段长度
% a 显著度
% 返回值:剔除粗大值后的数据
[m,n] = size(data);
if m > 1
data = data';
end
if length(data) <= l
out = NaN;
return;
end
out = data;
i1 = 1;
i2 = 1;
while ( i1 <= length(data)-l )
temp = data(i1:i1+l);
data_mean = mean(temp);
% v = temp - data_mean;
% 求方差
temp_std = std(temp);
% K由l、a查表所得
K = 2.24;
if abs(data(i1 + l) - data_mean) > K*temp_std
out(i2 + l) = NaN;
data(i1 + l)= [];
else
i1 = i1 + 1;
end
i2 = i2 + 1;
end
end
测试代码
data = [20.42 20.43 20.40 20.43 20.42 20.43 20.30 20.40 20.43 20.42 20.41 20.39 20.39 20.40 20.40 21.40 20.43 20.39 20.60 20.39 20.42 20.40 20.43];
data1= fun_romanovsky(data, 15, 0.05);
x = 1:length(data);
figure(2);
plot(x, data, 'b-', x , data1, 'ro');
legend('处理前','处理后');
效果图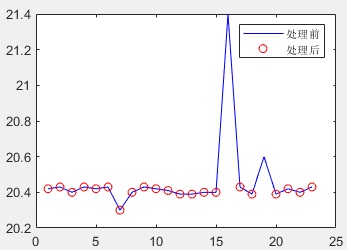
matlab-罗曼诺夫斯基准则剔除粗大值的更多相关文章
- 【Matlab编程】哈夫曼编码的Matlab实现
在前年暑假的时候,用C实现了哈夫曼编译码的功能,见文章<哈夫曼树及编译码>.不过在通信仿真中,经常要使用到Matlab编程,所以为了方便起见,这里用Matlab实现的哈夫曼编码的功能.至于 ...
- 柯尔莫可洛夫-斯米洛夫检验(Kolmogorov–Smirnov test,K-S test)
柯尔莫哥洛夫-斯米尔诺夫检验(Колмогоров-Смирнов检验)基于累计分布函数,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同. 在进行cumulative probab ...
- MATLAB 大数据剔除坏值
在用MATLAB进行数据分析的时候,坏点对正确结果的影响比较大, 因此,我么需要剔除野点,对于坏值的剔除,我们 利用 3σ准则 剔除无效数据: 3σ准则又称为拉依达准则,它是先假设一组检测数据只含有 ...
- 赫夫曼\哈夫曼\霍夫曼编码 (Huffman Tree)
哈夫曼树 给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离 ...
- 切诺夫界证明(Chernoff bound)
- Tikhonov regularization 吉洪诺夫 正则化
这个知识点很重要,但是,我不懂. 第一个问题:为什么要做正则化? In mathematics, statistics, and computer science, particularly in t ...
- x的奇幻之旅 (史蒂夫·斯托加茨 著)
第1部分 数字 第1章 数学:从企鹅的"鱼"订单到无穷大 (已看) 第2章 一组组石头与加减乘除运算 (已看) 第3章 "敌人的敌人就是朋友“与"负负得正&qu ...
- 诺塔斯读写卡QT SDK笔记
卡片操作函数调用 寻卡: Request --> LotusCardRequest 防撞处理: Anticollission --> LotusCardAnticoll 选卡: Selec ...
- matlab中如何根据t检验参数查找t检验值
这个问题花了一些时间.先看图 这个是t检验里面的公式,但是如何在matlab中找到该式子对应的值,我现在才知道. 就是这样:x=tinv(1-α/2,n-1)----t(n)分布的上侧α分位数 ...
随机推荐
- Struts2的学习-属性驱动和模型驱动
1.新建空项目,并托管到码云 2.设立maven 3.设置pom.xml 4.建包 5.在java包里建立两个类 package com.nf.entity; public class User { ...
- win7 64位 安装java jdk1.8 ,修改配置环境变量
下载jdk1.8,下载地址:http://www.wmzhe.com/soft-30118.html 安装时有两个程序,都安装在同一个目录下. win7 64位 安装java jdk1.8 ,修改配置 ...
- CentOS 7.3 下 Mysql(mariadb)的安装
LNMP的安装中 Nginx的安装很简单,我一般去Nginx官方网站上下载对应版本的rpm包后,上传到终端rpm安装.再此不多赘述. 但是在CentOS7中安装最新的mysql(mariadb)却经常 ...
- Scrum第三次冲刺
1.第三次冲刺任务概述 我们设计的长大万能通系统主要实现以下几个功能: a.周边查询 b.快递代取 c.查看校内新闻动态 d.二手物品交易 第三次冲刺我们计划实现周边查询功能.可以根据评分.距离最近. ...
- Jmeter入门15 JSON Assertion 适用于json格式的响应断言
当响应结果是json格式时,用JSON Assertion更方便判断. 1 在请求上右键添加json断言 2 编辑json Assertion 判断方式: 如果响应结果不是json格式的,fail ...
- 面条代码 vs. 馄沌代码
转载自:https://blog.csdn.net/godsme_yuan/article/details/6594013
- POJ 1632 Vase collection【状态压缩+搜索】
题目传送门:http://poj.org/problem?id=1632 Vase collection Time Limit: 1000MS Memory Limit: 10000K Total ...
- 【iOS】那些年,遇到的小坑
'NSInvalidArgumentException', reason: '-[__NSPlaceholderDictionary initWithObjectsAndKeys:]: second ...
- ASP.NET SignalR 与LayIM配合,轻松实现网站客服聊天室(四) 添加表情、群聊功能
休息了两天,还是决定把这个尾巴给收了.本篇是最后一篇,也算是草草收尾吧.今天要加上表情功能和群聊.基本上就差不多了,其他功能,读者可以自行扩展或者优化.至于我写的代码方面,自己也没去重构.好的,我们开 ...
- 【题解】洛谷P3399 丝绸之路
我丑,话说在前头 题目: https://www.luogu.org/problemnew/show/P3399 一道挺简单的DP 思路不难想 但是蒟蒻总是写错初始化啥的 思路 定义f[i][j]为第 ...
