[题解]N 皇后问题总结

N 皇后问题(queen.cpp)

[题目描述]

在 N*N 的棋盘上放置 N 个皇后（n<=10）而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上不能放置 2 个皇后） ，编程求解所有的摆放方法。

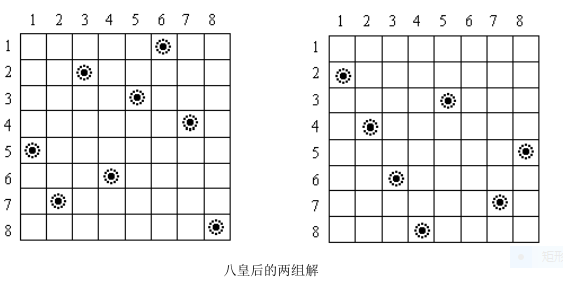
[输入格式]

输入：n

[输出格式]

每行输出一种方案，每种方案顺序输出皇后所在的列号，各个数之间有空格隔开。若无方案，则输出no solute!

[输入样例]

4

[输出样例]

2 4 1 3

3 1 4 2

[解法]

看题直接DFS即可.主要DFS方法是把每一行看作一个盒子,每层DFS只考虑当前盒子(即当前行)的皇后摆.当把n行每行的皇后位置确定后也就找到了一种方法. 下面是最重要的代码段:

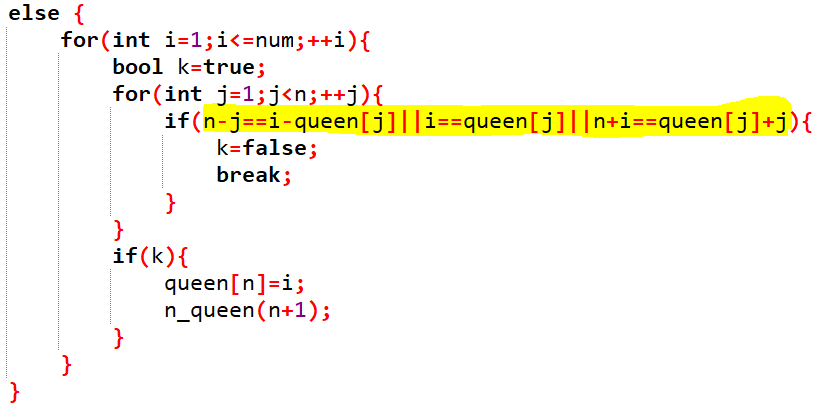
判断是否与之前的皇后攻击,因为是把每一行看作一个盒子所以不需要考虑行的皇后攻击.

[代码(AC)]

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <string>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 int queen[];
 int num;//num行
 bool flag=false;//判断是否有解标记
 void n_queen(int n){
         if(n>num){
             flag=true;//有解,更新标记
             for(int i=;i<=num;++i){//输出解
                 printf("%d ",queen[i]);
             }
             printf("\n");
         }
         else {
             for(int i=;i<=num;++i){
                 bool k=true;
                 for(int j=;j<n;++j){
                     if(n-j==i-queen[j]||i==queen[j]||n+i==queen[j]+j){//'\'斜||同一列||'/'斜
                         k=false;
                         break;
                     }
                 }
                 if(k){
                     queen[n]=i;//摆好这一行
                     n_queen(n+);//准备放下一行
                 }
             }
         }
 }
 int main(){
         //freopen("queen.in","r",stdin);
         //freopen("queen.out","w",stdout);
         memset(queen,false,sizeof(queen));
         scanf("%d",&num);
         n_queen();//从第一行放
         if(flag==false)printf("no solute!");
         return ;
 }

2018-10-05 22:20:16