【以2-SAT为主题的婚礼UVA11294】

·新娘头饰复杂，这个婚礼怪异非凡。

·英文题，述大意：

       婚宴上，有一个很长的桌子。桌子两边坐人（即人们坐成两排）。新娘坐在其中一排，只能看见桌子对面所有的人。输入的m表示有m对人打过架。在她快乐的眼睛里，不能出现以下情况：①有两个人是夫妻②有两个人打过架。询问是否存在一种座位编排方式满足条件。如果满足，还要输出与新娘同坐一排的人们（不含她）。

·分析：

       本题两个限制条件，有一共同点:如果A坐在桌子这边，那么B就必须坐在桌子另一边。理论化地，若A为真，则B为假/若B为真，则A为假。这样两种情况可进一步简化为：A为假或者B为假。（亦即两者各属一方）

·考虑一个美妙的简化问题：

       现有ABCD四个布尔变量，有以下要求：

     “A为假或者B为假,B为假或者D为假,D为假或者C为假”

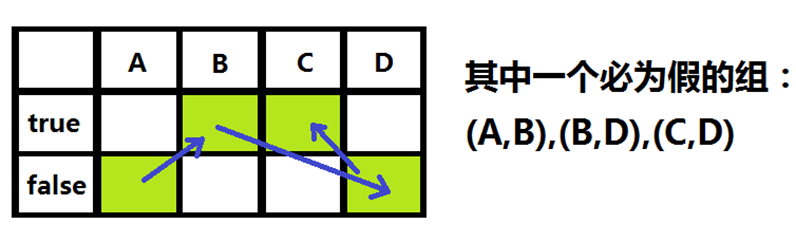
·如果我们令A为假，那么根据上述关系，就可以推出每个变量的值。

如果我们将这转化为一张图，每条边(u,v)表示如果u状态成立，那么v状态必须成立（例如：一条边可以是（A是假,B为真）），就可以很方便的用类似于染色的思想来完成：每走一步我们标记走过的结点，如果有一天标记的节点出现了(u为真)(u为假)两个点均被标记的情况，则说明是不合法的。

·细化思路：

重新注意“A为假或者B为假”。A为假不一定推出B一定为真，但是A为真就一定能推出B为假（2-SAT构图的关键）。因此，对于这样的条件，我们可以构造有向边：(A为真,B为假)。但是，如果你在慌乱之中构造了边：(A为假，B为真),那就错惨了（想一想，不为什么）。

·“构造一张有向图，其中每个变量i拆成2*i和i*2+1,分别表示该变量的假和真，最后要为每个变量选一种标记，使得整个图染色不会出现矛盾”

·我们统一所有的条件都是：“A为假或者B为假”。那么对于A,B标号的人，我们建边的方式为：(A*2+1,B*2)和(B*2+1,A*2)

·代码来临前的安宁：本题有一个“夫妻关系”，怎样处理？我们美妙地发现：如果将一对夫妇看成一个点，然后i*2,i*2+1直接表示这个点的真或假，我们再把真和假分别看成wife和husband,可以满足所有条件。不然，在正常情况下，夫妻要拆一次点，构造2-SAT要拆一次点，就不够美妙。如果偏要问在这个问题中，走到了点i*2或者i*2+1表达的是什么实际意义的话，那就是：走到了i*2表示第i对夫妇中，妻子和新娘坐一排；走到i*2+1表示丈夫和新娘坐一排。

 #include<stdio.h>
 #include<cstring>
 #define go(i,a,b) for(int i=a;i<=b;i++)
 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
 #define mem(a,b) memset(a,b,sizeof(a))
 const int N=;struct E{int v,next;}e[N*];
 int n,m,S[N],t,head[N],k;bool vis[N];
 void ADD(int u,int v){e[k]=(E){v,head[u^]};head[u^]=k++;}
 bool dfs(int u)
 {
     if(vis[u])return ;if(vis[u^])return ;vis[u]=;S[++t]=u;
     fo(i,head,u)if(!dfs(v))return ;return ;
 }
 int main(){while(scanf("%d%d",&n,&m)&&n&&m)
 {
     mem(head,);mem(vis,);k=;go(i,,m){int u,v;char c;
     scanf("%d%c",&u,&c);u=u*+(c=='h');
     scanf("%d%c",&v,&c);v=v*+(c=='h');ADD(u,v);ADD(v,u);}

     vis[]=;go(i,,n-){int u=i*;if(vis[u]||vis[u+])continue;
         t=;if(!dfs(u)){while(t)vis[S[t--]]=;
             if(!dfs(u+)){printf("bad luck\n");goto Judy;}}}
     go(i,,n-)printf("%d%c ",i,vis[i*]?'w':'h');puts("");Judy:;
 }return ;}//Paul_Guderian

我们的那捧车菊花，由深绿变成了金黄；

穿过那青葱的岁月，体验着不羁的彷徨。————汪峰《闪亮的日子》