一个蒟蒻对FFT的理解（蒟蒻也能看懂的FFT）

建议同学们先自学一下“复数（虚数）”的性质、运算等知识，不然看这篇文章有很大概率看不懂。

---

前言

作为一个典型的蒟蒻，别人的博客都看不懂，只好自己写一篇了。

膜拜机房大佬 HY

---

一. FFT是蛤？？

FFT (快速傅里叶变换) 的作用是在 O(nlogn) 时间算出多项式乘法的一个特别神奇的算法。

大家平时码的多项式乘法都是 O(n^2) 的吧

 #include<iostream>
 #include<cstdio>
 using namespace std;
 
 int n,m,a[],b[],c[];
 
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<n;i++)scanf("%d",a+i);
     for(int i=;i<m;i++)scanf("%d",b+i);
     for(int i=;i<n;i++)
     for(int j=;j<m;j++)c[i+j]+=a[i]*b[j];
     for(int i=;i<n+m-;i++)
         printf("%d ",c[i]);
 }

但这个算法并不能解决什么问题。

n<=100000 恭喜你，你成功TLE了，这时就要用到FFT了！！（是不是很激动？）

---

二. 算法思想

相信大家十分想知道这神奇的算法是怎么工作的。我们平时表达多项式的方法是系数表示法，而我们要把这个多项式换成另一个神奇的表达方法——点值表示法。这种神奇的表示法可以在 O(n) 的时间内算出多项式乘法，可是很遗憾，要想让这两种表示法互相转化任是需要 O(n^2) 的时间，而FFT的核心就是在 O(nlogn) 的时间内实现转换。

---

三. 系数表示法和点值表示法

系数表示法

就是用一个多项式的各个项的系数表示这个多项式，也就是我们平时所用的表示法。例如，我们可以这样表示：

f(x)=a₀+a₁x¹+a₂x²+..+a_nxⁿ⇔f(x)={a₀,a₁,a₂,..,a_n}

这就像是我们用数组存一个多项式一样

点值表示法

就是把这个多项式理解成一个函数，用这个函数上的若干个点的坐标来描述这个多项式。（两点确定一条直线，三点确定一条抛物线…同理n+1个点确定一个n次函数）

因此表示成这样：（注意：x[0]->x[n]是n+1个点）

f(x)=a₀+a₁x+a₂x²+..+a_nxⁿ⇔f(x)={(x₀,y₀),(x₁,y₁),(x₂,y₂),..,(x_n,y_n)}

为什么n+1个确定的点能确定一个唯一的多项式呢？你可以尝试着把这n+1个点的值分别代入多项式中：

如图，我们把相应的 x 与 y 的值代入，就能的到n+1个方程，也就能解出n+1个位置数，即数组 a，这样也就确定了一个多项式。

---

四. 点值表达式的乘法

现在，考虑这样一个问题，如果我有两个用点值表示的多项式，如何表示它们两个多项式的乘积呢？

我们令这两个点值表达式的 x 值相等，则会有一组唯一确定的 y 值。

f(x)={(x0,f(x0)),(x1,f(x1)),(x2,f(x2)),..,(xn,f(xn))}

g(x)={(x0,g(x0)),(x1,g(x1)),(x2,g(x2)),..,(xn,g(xn))}

F(x)={(x0,f(x1)*g(x0)),(x1,f(x1)*g(x1)),(x2,f(x2)*g(x2)),..,(xn,f(xn)*g(xn))}

结果F(x)=f(x)×g(x)，那么就有F(x0)=f(x0)∗g(x0)（x0x0为任意数）。

思考一下，很容易得出，如果 x 的取值相同，结果多项式的值就是两个因式的值的乘积

也就是说，如果我把两个函数的点值表示法中的 x 值相同的点的 y 值乘在一起就是它们的乘积（新函数）的点值表示。

这就可以O(n)计算多项式乘法。

---

五. 复数

我们把形如a+bi（a,b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当虚部等于零时，这个复数可以视为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。　　　————百度百科

这是复数的定义，不过为什么要用复数呢？？除非作者脑子有问题，不然肯定不会讲无关的东西

虽然点值表达式的乘法是O(n)的，可我们求的是系数表达式，而系数表达式与点值表达式的转换却是O(n^2)

复数的引用可以对这里进行优化。优化的方法我们下面再说。

我们给定一个坐标系，横轴表示 a，纵轴表示 b，这样所有的复数都可以在这里表示出来，这便是复数的几何意义。更多关于复数的内容请自行了解在这就不阐述了

然后，思考一个简单的问题：两个复数的乘法有没有某种特定的几何意义？（只是一个数学性质，在此不进一步深究，可用三角函数证明。)

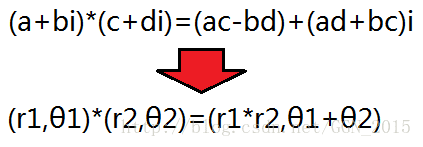
如图可得，复数的乘法，长度相乘，极角相加。

---

六. 单位复根

现在，回到我们刚才讲到的“点值表示法”的问题，要想转化，也就是要解一个n+1元的方程组。

当我们计算x₀，x₀²，...，x₀ⁿ 时会浪费大量的时间。这个数学运算看似是没有办法加速的，而实际上我们可以找到一种神奇的“x值”，带进去之后不用反复地去做无用n次方操作，比如 1 与 -1，可以加速。

但是我们要至少带进去n+1个不同的数才能进行系数表示。这时就要用到复数了！

我们需要的是满足“ω^k=1”的数（k为整数）

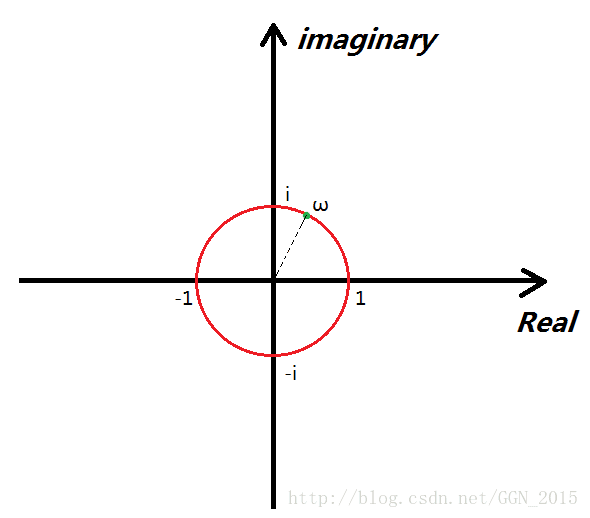
看上图中的红圈，红圈上的每一个点距原点的距离都是1个单位长度，所以说如果说对这些点做k次方运算，它们始终不会脱离这个红圈。

因为它们在相乘的时候r始终=1，只是θ的大小在发生改变。而这些点中有无数个点经过k次方之后可以回到“1”。

因此，我们可以把这样的一组神奇的x带入函数求值。像这种能够通过k次方运算回到“1”的数，我们叫它“复根”用“ω”表示。

你会发现：其实k次负根就相当于是给图中的圆周平均分成k个弧，弧与弧之间的端点就是“复根”，我们只需要知道ω_n¹，就能求出ω_n^k。所以我们称“ω_n¹”为“单位复根”。
其实，我们用“ω_k”表示单位复根，ω_k¹表示的是“单位复根”的“1次方”也就是它本身，其他的就叫做 k 次单位复根的 n 次方。

---

七. FFT 之 DFT

前面的复数都是数学的内容，所以讲的比较简略，不过也终于到正题 FFT 了！

DFT 是 FFT 中将系数表达式转变为点值表达式的过程。

我们把多项式的系数表达式，换成 x 值 为 ω_n^k 的点值表达式。

f(x)=a₀ + a₁*x + a₂*x² + a₃*x³ + ...... + a_n-1*x^n-1

f(x)={(ω_n⁰,y₀),(ω_n¹,y₁),(ω_n²,y₂), ...... ,(ω_n^n-1,y_n-1)}

然后我们可以将 x 值（ω_n^k）省略，只储存 y₀ , y₁ , ......， y_n

可我们将 ω_n^k 带入 x 后又能怎么优化呢？我们可以尝试一下分治思想。

将 ω_n^k 和 ω_n^k+n/2​​ 代入，就可以发现一个神奇的现象

F(    ω_n^k   )=G(ω_n^2k)+ω_n^k * H(ω_n^2k)

　　　　　=G(ω_n^2k) + ω_n^k * H(ω_n^2k)

　　　　　=G(ω_n/2^k) + ω_n^k * H(ω_n/2^k)

F(ω_n^k+n/2)=G(ω_n^2k+n) + ω_n^k+n/2 * H(ω_n^2k+n)

　　　　　=G(ω_n^2k * ω_nⁿ) - ω_n^k * H(ωn^2k * ω_nⁿ)

　　　　　=G(ω_n^2k) - ω_n^k * H(ω_n^2k)

　　　　   =G(ω_n/2^k) - ω_n^k * H(ω_n/2^k)

没想到得出来的式子竟然这么相近，也就是说，我们把其中一个值带入，就可以的到另一个，我们就可以把时间缩小一半了。

接下来就可以递归求解了！！！

 const double PI=acos(-);    //圆周率 π
 typedef complex<double> cmplx;//我比较懒，就用了STL自带的复数类
 void DFT(int len,cmplx a[]){
     if(len==)return;    //只有一个常数项
     cmplx a1[len>>],a2[len>>];
     for(int i=;i<=len;i+=)    //根据下标的奇偶性分类
         a1[i>>]=a[i],a2[i>>]=a[i+];
     FFT(len>>,a1),FFT(len>>,a2);
     cmplx W=exp(cmplx(,PI/len));//求为单位根ω
     cmplx w=cmplx(,);    //w表示0~n-1次幂，初始为0次幂 1
     for(int i=;i<(len>>);i++,w=w*W){
         a[i]=a1[i]+w*a2[i];        //上文我们推导的性质
         a[i+(len>>)]=a1[i]-w*a2[i];
         //利用单位根的性质，O(1)得到另一部分
     }
 }

是不是很友好？可是递归实现的缺点也很显著，空间都消耗巨大，所以我们就要模拟递归了。

递归的时候，我们是将多项式奇偶拆开，如图

这看似拆出来没什么规律，但我们试着把数换为二进制，又会发生什么呢？

拆完后的多项式竟然是原来的二进制翻转！！！我们就可以这样通过倍增来模拟递归了！！！

 const double PI=acos(-);
 typedef complex<double> cmplx;
 
 void get_rev(){        //求二进制反转
     while(bit<=n)bit<<=;    //bit为最大二进制位长度的值
     for(int i=;i<bit;i++)
     rev[i]=(rev[i>>]>>)|(i&)*(bit>>);
 }
 
 void DFT(cmplx a[]){
     for(int i=;i<bit;i++)
         if(i<rev[i])swap(a[i],a[rev[i]]);
     //根据rev数组进行二进制反转
     for(int i=;i<bit;i<<=){    //倍增模拟递归
         cmplx W=exp(cmplx(,PI/i));
         for(int j=;j<bit;j+=i<<){    //一组一组处理
             cmplx w(,);  //同递归版代码
             for(int k=j;k<j+i;k++,w*=W){ //同递归版代码
                 cmplx x=a[k];
                 cmplx y=w*a[k+i];
                 a[k]=x+y,a[k+i]=x-y;
             }
         }
     }
 }

虽然丑了，不过优秀了许多。

---

八. FFT 之 IDFT

我们将系数表示法转为点值表示法，总要把它变回来，而变回来的过程就是 IDFT 了。

IDFT似乎要矩阵的知识证明（而我不会，尴不尴尬），于是乎，我就只亮一波代码好了！

 void IDFT(cmplx a[]){
     for(int i=;i<bit;i++)
         if(i<rev[i])swap(a[i],a[rev[i]]);
     for(int i=;i<bit;i<<=){
         cmplx W=exp(cmplx(,-PI/i));
         for(int j=;j<bit;j+=i<<){
             cmplx w(,);
             for(int k=j;k<j+i;k++,w*=W){
                 cmplx x=a[k];
                 cmplx y=w*a[k+i];
                 a[k]=x+y,a[k+i]=x-y;
             }
         }
     }
     for(int i=;i<bit;i++)a[i]/=bit;
 }

你会发现，这只是几个符号的差别（所以你也不是很必要知道原理了吧，好奇的同学只能自己探索了）

其实我们可以吧 DFT 和 IDFT 合并成一个函数

 void FFT(cmplx a[],int dft){  //1是DFT，-1是IDFT
     for(int i=;i<bit;i++)
         if(i<rev[i])swap(a[i],a[rev[i]]);
     for(int i=;i<bit;i<<=){
         cmplx W=exp(cmplx(,dft*PI/i));
         for(int j=;j<bit;j+=i<<){
             cmplx w(,);
             for(int k=j;k<j+i;k++,w*=W){
                 cmplx x=a[k];
                 cmplx y=w*a[k+i];
                 a[k]=x+y,a[k+i]=x-y;
             }
         }
     }
     if(dft==-)for(int i=;i<bit;i++)a[i]/=bit;
 }

---

九. 总结

法法塔到这也就结束了，没什么好说，再亮一波FFT代码

洛谷 P3803 【模板】多项式乘法（FFT）

 #include<iostream>
 #include<cstdio>
 #include<complex>
 using namespace std;
 
 const double PI=acos(-);
 typedef complex<double> cmplx;
 cmplx a[],b[];
 int m,n,x,bit=,rev[];
 int output[];
 
 void get_rev(){
     for(int i=;i<bit;i++)
     rev[i]=(rev[i>>]>>)|(bit>>)*(i&);
 }
 
 void FFT(cmplx *a,int dft){
     for(int i=;i<bit;i++)
         if(i<rev[i])swap(a[i],a[rev[i]]);
     for(int i=;i<bit;i<<=){
         cmplx W=exp(cmplx(,dft*PI/i));
         for(int j=;j<bit;j+=i<<){
             cmplx w(,);
             for(int k=j;k<j+i;k++,w=w*W){
                 cmplx x=a[k];
                 cmplx y=w*a[k+i];
                 a[k]=x+y,a[k+i]=x-y;
             }
         }
     }
     if(dft==-)
     for(int i=;i<bit;i++)a[i]/=bit;
 }
 
 int main(){
     scanf("%d%d",&n,&m);
     while(bit<=n+m)bit<<=;
     for(int i=;i<=n;i++)
         scanf("%d",&x),a[i]=x;
     for(int i=;i<=m;i++)
         scanf("%d",&x),b[i]=x;
     get_rev();
     FFT(a,),FFT(b,);
     for(int i=;i<bit;i++)a[i]*=b[i];
     FFT(a,-);
     for(int i=;i<bit;i++)
         output[i]+=a[i].real()+0.5;
     for(int i=;i<=n+m;i++)
         printf("%d ",output[i]);
 }

谢谢大家，终于完工了！！！2018-04-27 20:35:26