LDA和PCA

LDA：

LDA的全称是Linear Discriminant Analysis（线性判别分析），是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant，因为它被Ronald Fisher发明自1936年，Discriminant这次词我个人的理解是，一个模型，不需要去通过概率的方法来训练、预测数据，比如说各种贝叶斯方法，就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法，据我所知，百度的商务搜索部里面就用了不少这方面的算法。

LDA的原理是，将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：

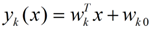
当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。对于每一个分类，都有一个公式去算一个分值，在所有的公式得到的分值中，找一个最大的，就是所属的分类了。

上式实际上就是一种投影，是将一个高维的点投影到一条高维的直线上，LDA最求的目标是，给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开，当k=2即二分类问题的时候，如下图所示：

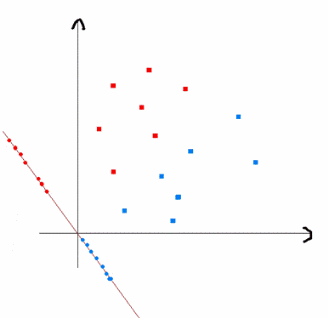
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和蓝色的点被原点明显的分开了，这个数据只是随便画的，如果在高维的情况下，看起来会更好一点。下面我来推导一下二分类LDA问题的公式：

假设用来区分二分类的直线（投影函数)为：

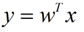
LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们需要定义几个关键的值。

类别i的原始中心点为：（Di表示属于类别i的点)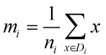

类别i投影后的中心点为：

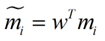
衡量类别i投影后，类别点之间的分散程度（方差）为：

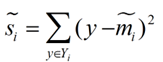
最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

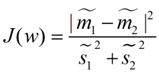
我们分类的目标是，使得类别内的点距离越近越好（集中），类别间的点越远越好。分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，我们最大化J(w)就可以求出最优的w了。想要求出最优的w，可以使用拉格朗日乘子法，但是现在我们得到的J(w)里面，w是不能被单独提出来的，我们就得想办法将w单独提出来。

我们定义一个投影前的各类别分散程度的矩阵，这个矩阵看起来有一点麻烦，其实意思是，如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近，则Si里面元素的值就越小，如果分类的点都紧紧地围绕着mi，则Si里面的元素值越更接近0.

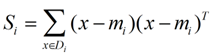
带入Si，将J(w)分母化为：

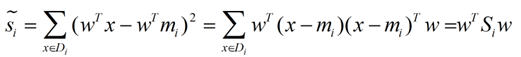
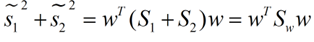
同样的将J(w)分子化为：

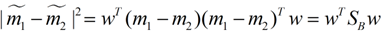
这样损失函数可以化成下面的形式：

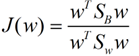
这样就可以用最喜欢的拉格朗日乘子法了，但是还有一个问题，如果分子、分母是都可以取任意值的，那就会使得有无穷解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧，在下面将说的PCA里面也会用到，如果忘记了，请复习一下高数），并作为拉格朗日乘子法的限制条件，带入得到：

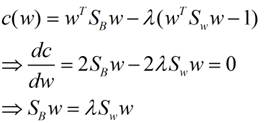
这样的式子就是一个求特征值的问题了。

对于N(N>2)分类的问题，我就直接写出下面的结论了：

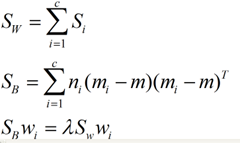
这同样是一个求特征值的问题，我们求出的第i大的特征向量，就是对应的Wi了。

这里想多谈谈特征值，特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用，特征值表示的是矩阵的性质，当我们取到矩阵的前N个最大的特征值的时候，我们可以说提取到的矩阵主要的成分（这个和之后的PCA相关，但是不是完全一样的概念）。在机器学习领域，不少的地方都要用到特征值的计算，比如说图像识别、pagerank、LDA、还有之后将会提到的PCA等等。

下图是图像识别中广泛用到的特征脸（eigen face），提取出特征脸有两个目的，首先是为了压缩数据，对于一张图片，只需要保存其最重要的部分就是了，然后是为了使得程序更容易处理，在提取主要特征的时候，很多的噪声都被过滤掉了。跟下面将谈到的PCA的作用非常相关。

特征值的求法有很多，求一个D * D的矩阵的时间复杂度是O(D^3), 也有一些求Top M的方法，比如说power method，它的时间复杂度是O(D^2 * M), 总体来说，求特征值是一个很费时间的操作，如果是单机环境下，是很局限的。

PCA：

主成分分析（PCA）与LDA有着非常近似的意思，LDA的输入数据是带标签的，而PCA的输入数据是不带标签的，所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在，给定了训练数据后，将会得到一系列的判别函数（discriminate function），之后对于新的输入，就可以进行预测了。而PCA更像是一个预处理的方法，它可以将原本的数据降低维度，而使得降低了维度的数据之间的方差最大（也可以说投影误差最小，具体在之后的推导里面会谈到）。

方差这个东西是个很有趣的，有些时候我们会考虑减少方差（比如说训练模型的时候，我们会考虑到方差-偏差的均衡），有的时候我们会尽量的增大方差。方差就像是一种信仰（强哥的话），不一定会有很严密的证明，从实践来说，通过尽量增大投影方差的PCA算法，确实可以提高我们的算法质量。

说了这么多，推推公式可以帮助我们理解。我下面将用两种思路来推导出一个同样的表达式。首先是最大化投影后的方差，其次是最小化投影后的损失（投影产生的损失最小）。

    最大化方差法：

假设我们还是将一个空间中的点投影到一个向量中去。首先，给出原空间的中心点：

   
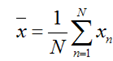
假设u1为投影向量，投影之后的方差为：

   
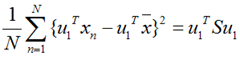
上面这个式子如果看懂了之前推导LDA的过程，应该比较容易理解，如果线性代数里面的内容忘记了，可以再温习一下，优化上式等号右边的内容，还是用拉格朗日乘子法：

   
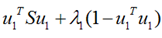
将上式求导，使之为0，得到：

   
这是一个标准的特征值表达式了，λ对应的特征值，u对应的特征向量。上式的左边取得最大值的条件就是λ1最大，也就是取得最大的特征值的时候。假设我们是要将一个D维的数据空间投影到M维的数据空间中（M < D)， 那我们取前M个特征向量构成的投影矩阵就是能够使得方差最大的矩阵了。

    最小化损失法：

假设输入数据x是在D维空间中的点，那么，我们可以用D个正交的D维向量去完全的表示这个空间（这个空间中所有的向量都可以用这D个向量的线性组合得到）。在D维空间中，有无穷多种可能找这D个正交的D维向量，哪个组合是最合适的呢？

假设我们已经找到了这D个向量，可以得到：

   
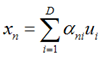
我们可以用近似法来表示投影后的点：

   
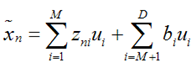
上式表示，得到的新的x是由前M 个基的线性组合加上后D - M个基的线性组合，注意这里的z是对于每个x都不同的，而b对于每个x是相同的，这样我们就可以用M个数来表示空间中的一个点，也就是使得数据降维了。但是这样降维后的数据，必然会产生一些扭曲，我们用J描述这种扭曲，我们的目标是，使得J最小：

   
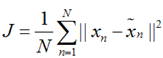
上式的意思很直观，就是对于每一个点，将降维后的点与原始的点之间的距离的平方和加起来，求平均值，我们就要使得这个平均值最小。我们令：

   
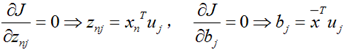
将上面得到的z与b带入降维的表达式：

   
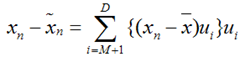
将上式带入J的表达式得到：

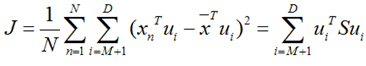    再用上拉普拉斯乘子法（此处略），可以得到，取得我们想要的投影基的表达式为：

   
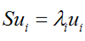
这里又是一个特征值的表达式，我们想要的前M个向量其实就是这里最大的M个特征值所对应的特征向量。证明这个还可以看看，我们J可以化为：

   
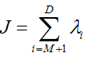
也就是当误差J是由最小的D - M个特征值组成的时候，J取得最小值。跟上面的意思相同。