Codeforces Gym100543B 计算几何 凸包 线段树 二分/三分 卡常

原文链接https://www.cnblogs.com/zhouzhendong/p/CF-Gym100543B.html

题目传送门 - CF-Gym100543B

题意

　　给定一个折线图，对于每一条折线，问沿着这条折线往右看第一个看到的线段的编号（如果视线恰好看到上端点，则当没看见）

　　放张图片助于理解：

　　

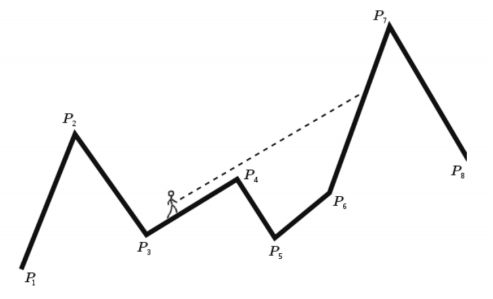
　　折线图用 $n$ 个点来描述。

　　$n\leq 100000,\ \ \ \ 坐标范围：(x,y)|0\leq x,y\leq 10^9$

题解

　　这题好妙啊。

　　首先一个结论：如果射线与一段区间的点形成的上凸壳相交，那么他一定与这段区间内的折线段相交。

　　我们只需要建个线段树，所有节点上建一个当前节点所表示的区间内的点构成的上凸壳，然后每次 $O(\log^2 n)$ 询问即可。

　　如何 $O(\log^2 n)$ 询问？

　　首先，线段树一只 $\log$ 。

　　我们需要支持的是一只 $\log$ 判断射线是否与上凸壳相交。

　　显然原线段与上凸壳的点的叉积是一个单峰函数。（根据叉积的定义，平行四边形的低不变，高为单峰函数，故面积也为单峰函数）

　　于是显然可以三分搞定。

　　但是被卡常数了。

　　于是 foreverpiano 告诉了我一种巧妙的二分做法。

　　（这里求叉积的点依次是线段左侧点，线段右侧点，当前点）

　　对于每一次的 $mid$ ，我们看一看 原线段与凸壳上面的第 $mid$ 和 $mid+1$ 个点的叉积大小，分别记为 $v1$ 和 $v2$。

　　如果 $v1>v2$ 则令 $R=mid-1$ 否则令 $L=mid+1$ 。

　　注意一旦有 $v1>0$ 或者 $v2>0$ 就可以判断一定相交了。如果这个时候不return，则可能会有漏算。

　　然后区间极小的时候暴力判。

　　然后常数小了好多。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=100005;
int T,n;
struct Point{
	int x,y;
	Point(){}
	Point(int _x,int _y){
		x=_x,y=_y;
	}
}p[N],P[N];
vector <int> s[N<<3];
LL cross(Point a,Point b,Point c){
	return 1LL*(b.x-a.x)*(c.y-a.y)-1LL*(c.x-a.x)*(b.y-a.y);
}
int read(){
	char ch=getchar();
	int x=0;
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+ch-48,ch=getchar();
	return x;
}
int st[N],top;
void Get_convex(vector <int> &s,int L,int R){
	st[top=1]=R,st[++top]=R-1;
	for (int i=R-2;i>=L;i--){
		while (top>1&&cross(p[st[top-1]],p[st[top]],p[i])<=0)
			top--;
		st[++top]=i;
	}
	s.clear();
	for (int i=top;i>0;i--)
		s.push_back(st[i]);
}
void build(int rt,int L,int R){
	if (L==R){
		s[rt].clear();
		s[rt].push_back(L);
		return;
	}
	Get_convex(s[rt],L,R);
	int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
	build(ls,L,mid);
	build(rs,mid+1,R);
}
int Query(Point a,Point b,vector <int> &s){
	int L=0,R=s.size()-1,mid;
	while (L+3<=R){
		mid=(L+R)>>1;
		LL x=cross(a,b,p[s[mid]]),y=cross(a,b,p[s[mid+1]]);
		if (x>0||y>0)
			return 1;
		if (x>y)
			R=mid-1;
		else
			L=mid+1;
	}
	int now=-1;
	for (int i=L;i<=R;i++)
		if (cross(a,b,p[s[i]])>0)
			return 1;
	return 0;
}
int Query(int rt,int L,int R,int xL,int xR){
	if (xL>xR||L>xR||R<xL||!Query(p[xL-2],p[xL-1],s[rt]))
		return 0;
	if (L==R)
		return L-1;
	int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
	int now=Query(ls,L,mid,xL,xR);
	return now?now:Query(rs,mid+1,R,xL,xR);
}
int main(){
	T=read();
	while (T--){
		n=read();
		for (int i=1;i<=n;i++)
			p[i].x=read(),p[i].y=read();
		build(1,1,n);
		for (int i=1;i<n;i++){
			cout << Query(1,1,n,i+2,n);
			if (i<n-1)
				putchar(' ');
		}
		puts("");
	}
	return 0;
}