机器学习之MCMC算法

1、MCMC概述

　　从名字我们可以看出，MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。之前已经介绍过蒙特卡洛方法，接下来介绍马尔科夫链，以及结合两者的采样算法。

2、马尔科夫链

　　马尔科夫链的概念在很多地方都被提及过，它的核心思想是某一时刻状态转移的概率只依赖于它的前一个状态。　　

　　我们用数学定义来描述，则假设我们的序列状态是...X_t−2, X_t−1, X_t, X_t+1,...，那么我们的在时刻X_t+1的状态的条件概率仅仅依赖于时刻X_t，即：

　　

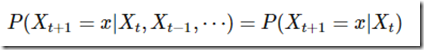
　　既然某一时刻状态转移的概率只依赖于它的前一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。状态转移情况如下图所示

　　

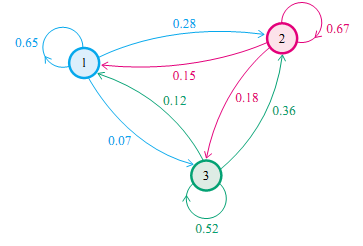
　　则状态转移矩阵可以表示为

　　

　　此时，我们给定一个初始状态，然后经过该状态转移矩阵的转换，最终会收敛到一个稳定的状态，具体如马尔科夫链定理所示

　　

　　由于马尔科夫链能收敛到平稳分布， 于是有了一个想法：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x₀出发沿着马氏链转移, 得到一个转移序列 x₀, x₁, x₂,⋯x_n, x_n+1⋯， 如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本x_n, x_n+1⋯（也就是从第n步收敛时开始，之后的x都服从同一个平稳分布，我们可以将这个分布设定为我们的目标采样分布）。

　　从上面可以看出马尔科夫链的平稳分布收敛主要依赖于状态转移矩阵，所以关键是如何构建状态转移矩阵，使得最终的平稳分布是我们所要的分布。想做到这一点主要依赖于细致平稳定理

　　

3、MCMC采样和M-H采样

　　在MCMC采样中先随机一个状态转移矩阵Q，然而该矩阵不一定能满足细致平稳定理，一次会做一些改进，具体过程如下

　　

　　MCMC采样算法的具体流程如下

　　

　　然而关于MCMC采样有收敛太慢的问题，所以在MCMC的基础上进行改进，引出M-H采样算法

　　

　　M-H算法的具体流程如下

　　

　　M-H算法在高维时同样适用

　　

　　一般来说M-H采样算法较MCMC算法应用更广泛，然而在大数据时代，M-H算法面临着两个问题：

　　1）在高维时的计算量很大，算法效率很低，同时存在拒绝转移的问题，也会加大计算量

　　2）由于特征维度大，很多时候我们甚至很难求出目标的各特征维度联合分布，但是可以方便求出各个特征之间的条件概率分布（因此就思考是否能只知道条件概率分布的情况下进行采样）。

4、Gibbs采样

　　

　　

　　因此可以得出在二维的情况下Gibbs采样算法的流程如下

　　

　　而在多维的情况下，比如一个n维的概率分布π(x₁, x₂, ...x_n)，我们可以通过在n个坐标轴上轮换采样，来得到新的样本。对于轮换到的任意一个坐标轴xi上的转移，马尔科夫链的状态转移概率为P(x_i|x₁, x₂, ..., x_i−1, x_i+1, ..., x_n)，即固定n−1个坐标轴，在某一个坐标轴上移动。而在多维的情况下Gibbs采样算法的流程如下

　　

　　由于Gibbs采样在高维特征时的优势，目前我们通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的，这时M-H采样仍然成立。