POJ 2823 滑动窗口 单调队列

https://vjudge.net/problem/POJ-2823

中文：https://loj.ac/problem/10175

题目

给一个长度为 $N$ 的数组，一个长为 $K$ 的滑动窗体从最左端移至最右端，你只能看到窗口中的 $K$ 个数，每次窗体向右移动一位，你的任务是找出窗体在各个位置时的最大值和最小值。

题解

滑动窗口模板题……

直接抄紫书上的话……

窗口滑动时，首先删除窗口最左边元素（如果是有用元素），然后把新元素加入单调队列。注意，比新元素大的元素都变得无用了，应当从右往左删除。

举个例子……

窗口初始状态

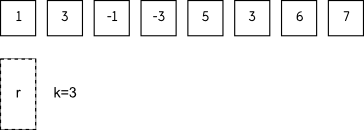
向右扫描

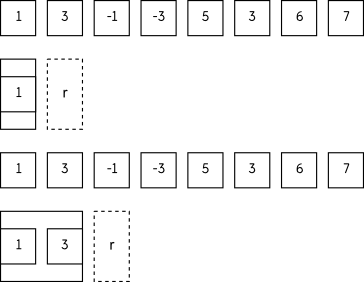
每次加入新元素到窗口就从右边删掉所有大于这个值的元素

继续……

到这里-1算有用的元素了，会删掉……

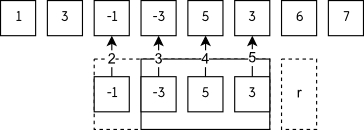
$5-2\geqslant k=3$ ，表示这个位置已经不在窗口内了……

为了存位置需要新开一个数组，既然这样干脆窗口里直接存位置就行了，比较的时候通过下标使用就好。

另外在删除的时候可以使用二分确定要删除到的位置，两个循环其实可以合并为一个。

TLE代码（其实用C++交就会AC，用G++才TLE，用快速读写优化就可以AC了）

另外这个代码是主要考虑减少时间使用去了= =显然实际应该考虑三者平衡（时间、空间、编程）……

#include<iostream>
#include<cstdio>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...)
#endif

#define MAXN 1000007

int arr[MAXN], que[MAXN], l, r;
int n,k;

int main() {
	#ifdef sahdsg
	freopen("in.txt", "r", stdin);
	#endif
	scanf("%d%d", &n, &k);
	REP(i,0,n) {
		scanf("%d", &arr[i]);
	}
	l=0, r=0;
	REP(i,0,k-1) {
		while(l<r && arr[que[r-1]]>arr[i]) r--;
		que[r++] = i;
	}
	bool fi = false;
	REP(i,k-1,n) {
		if(que[l]<=i-k) l++;
		while(l<r && arr[que[r-1]]>arr[i]) r--;
		que[r] = i;
		if(fi) putchar(' '); else fi = true;
		printf("%d", arr[que[l]]);
		r++;
	}
	putchar('\n');

	fi = false;
	l=0, r=0;
	REP(i,0,k-1) {
		while(l<r && arr[que[r-1]]<arr[i]) r--;
		que[r++] = i;
	}
	REP(i,k-1,n) {
		if(que[l]<=i-k) l++;
		while(l<r && arr[que[r-1]]<arr[i]) r--;
		que[r] = i;
		if(fi) putchar(' '); else fi = true;
		printf("%d", arr[que[l]]);
		r++;
	}
	return 0;
}

AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...)
#endif

#define MAXN 1000007

int arr[MAXN], que[MAXN], l, r;
int n,k;

template <class T>
inline void read(T& x) {
    char c=getchar();int f=1;x=0;
    while(!isdigit(c)&&c!='-')c=getchar();if(c=='-')f=-1,c=getchar();
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}x*=f;
}
void write(int x) {
    if(x<0) {putchar('-');write(-x);return;}
    if(x>9) write(x/10); putchar(x%10+'0');
}

int main() {
	#ifdef sahdsg
	freopen("in.txt", "r", stdin);
	#endif
	read(n); read(k);
	REP(i,0,n) {
		read(arr[i]);
	}
	l=0, r=0;
	REP(i,0,k-1) {
		while(l<r && arr[que[r-1]]>arr[i]) r--;
		que[r++] = i;
	}
	bool fi = false;
	REP(i,k-1,n) {
		if(que[l]<=i-k) l++;
		if(l<r && arr[que[r-1]]>arr[i]) {
			int fl=l, fr=r;
			while(fr>fl) {
				int mid=fl+((fr-fl)>>1); //[l, m) [m,r)
				if(arr[que[mid]]>arr[i]) {
					fr=mid;
				} else {
					fl=mid+1;
				}
			}
			r=fr;
		}
		que[r++] = i;
		if(fi) putchar(' '); else fi = true;
		write(arr[que[l]]);
	}
	putchar('\n');

	fi = false;
	l=0, r=0;
	REP(i,0,k-1) {
		while(l<r && arr[que[r-1]]<arr[i]) r--;
		que[r++] = i;
	}
	REP(i,k-1,n) {
		if(que[l]<=i-k) l++;
		if(l<r && arr[que[r-1]]<arr[i]) {
			int fl=l, fr=r;
			while(fr>fl) {
				int mid=fl+((fr-fl)>>1); //[l, m) [m,r)
				if(arr[que[mid]]<arr[i]) {
					fr=mid;
				} else {
					fl=mid+1;
				}
			}
			r=fr;
		}
		que[r++] = i;
		if(fi) putchar(' '); else fi = true;
		write(arr[que[l]]);
	}
	return 0;
}