5.2 CUDA Histogram直方图

什么是Histogramming

Histogramming是一种从大的数据集中提取典型特征和模式的方式.

在统计学中，直方图（英语：Histogram）是一种对数据分布情况的图形表示，是一种二维统计图表，它的两个坐标分别是统计样本和该样本对应的某个属性的度量。

图像直方图（英语：Image Histogram）是用以表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素数。可以借助观察该直方图了解需要如何调整亮度分布。这种直方图中，横坐标的左侧为纯黑、较暗的区域，而右侧为较亮、纯白的区域。因此，一张较暗图片的图像直方图中的数据多集中于左侧和中间部分；而整体明亮、只有少量阴影的图像则相反。

很多数码相机提供图像直方图功能，拍摄者可以通过观察图像直方图了解到当前图像是否过分曝光或者曝光不足。

计算机视觉领域常借助图像直方图来实现图像的二值化。

颜色直方图

在图像处理和摄影领域中，颜色直方图（英语：Color Histogram）指图像中颜色分布的图形表示。数字图像的颜色直方图覆盖该图像的整个色彩空间，标绘各个颜色区间中的像素数。

颜色直方图本身可以针对任意色彩空间使用，但这一术语通常只用在诸如 RGB 和 HSV 的三维色彩空间，而针对灰度图像时常使用亮度直方图（英语：Intensity Histogram）这一术语。

直方图例子

比如一个句子"Programming Massively Parallel Processors",我们构建一个字母出现频率的直方图.

A(4次), C(1), E(1), G(1), ...

Host端我们做统计的话,就会构建26大小的数组来表示a-z,然后遍历这个句子,碰到不同的case进行累加操作.

Device端并行化: 把这个sentense 划分成多个block,每个block统计自己的情况,同意保存到一个数组里面.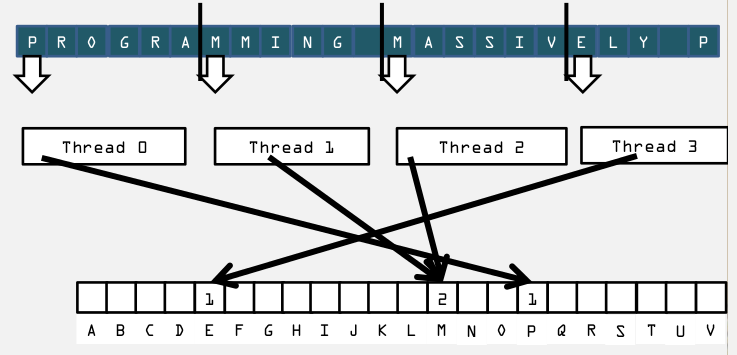

但是当两个thread同事在对A做+1的动作后,最后的结果是1,而正确的结果是2才对,这时候需要使用原子加操作:
unsigned int atomicAdd(unsigned int* address, unsigned int val);

其实在CUDA的device中执行计数的功能都需要使用原子操作才行.

优化histor kernel代码:

不使用shared memory的情况下,执行原子操作,无论有多少个thread,在这个例子中最多同时执行的只有256,其他的都因为原子操作需要等待, 所以这里每个thread block使用一个 shared memory,  统计每个thread block,然后最后一起copy 给 histo

__global__ void histo_kernel(unsigned char *buffer, long size, unsigned int *histo)
{
    __shared__ unsigned int histo_private[];
    if(threadId.x < )  //初始化shared histo
        histo_private[threadIdx.x] = ;
    __syncthread();

    int i = threadIdx.x + blockIdx.x * blockDim.x;
    // 步长是所有threads的数目
    int stride = blockDim.x * gridDim.x;
    while(i < size) {
        atomicAdd(&(private_histo[buffer[i]]), );
        i + = stride;
    }

    //等待所有线程执行完
    __syncthreads();

    if(threadIdx.x < ){
        atomicAdd(&(histo[threadIdx.x]), private_histo[threadIdx.x]);
    }
}