欧拉工程第66题：Diophantine equation

题目链接

脑补知识：佩尔方差

上面说的貌似很明白，最小的i，对应最小的解

然而我理解成，一个循环的解了，然后就是搞不对，后来，仔细看+手工推导发现了问题。i从0开始变量，知道第一个满足等式的解就是最小解。

问题转化为求根号n的连分数问题，分子就是x，分母就是y

要求的分子，分母，问题又转化为：根号n的连分数表示，对，求出其连分数表示就OK了

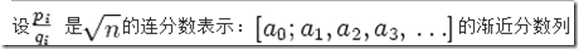
先求出a的序列是什么？

第64题，就是求a的序列的。

a求出来了，要求出分子分母的表达式。

第65题，就是已经知道了a的序列，求分子，当然也可以求分母的

分子，分母求出来了，在验证：X*X-D*Y*Y=1时候就是最小解

问题真是一环套一环的。

Python程序：

import time as time 

start = time.time()

def getD(N):
    x_max ,y_max= 0,0
    D = 0
    x,y = 0,0
    for S in range(2,N+1):
        x,y = resolve(S)
        if x>x_max:
            x_max ,y_max= x,y
            D = S
    return D,x_max,y_max

def resolve(S):
    m = 0
    d = 1
    a0 = int(S**0.5)
    if a0*a0 == S :return -1,-1;
    a= a0
    li = [a]
    x,y = 1,1
    while x*x-S*y*y!=1:
        m = d*a - m
        d = (S - m*m)/d
        a = int((a0 + m)/d)
        li.append(a)
        x = getX(li)
        y = getY(li)
#     print li
    return x,y;

def getX(li):
    x0 = 1
    x1 = li[0]
    li = li[1:]
    for l in li:
        x = l * x1 + x0
        x0 = x1
        x1 = x
    return x 

def getY(li):
    y0 = 0
    y1 = 1
    li = li[1:]
    for l in li:
        y = l * y1 + y0
        y0 = y1
        y1 = y
    return y 

if __name__ == '__main__':

    start = time.time()
    N = 1000
    D ,x_max,y_max= getD(N)
    print "running time={0}seconds,D={1},x_max={2},y_max={3}".format(time.time()-start,D,x_max,y_max)

求的是最小解X的最大值时候的D，答案是661

然而：

x_max=16421658242965910275055840472270471049

y_max=638728478116949861246791167518480580

这个值好大的

附一：python程序：

from math import sqrt
from time import time

def prefect_sqrt(n):
    return int(sqrt(n))**2 == n 

def floor_root(n):
    return int(sqrt(n))

def chakravals(n):
    x_max = 0
    for d in range(2,n+1):
        if not prefect_sqrt(d):
            p1 = floor_root(d)
            q1 = 1
            m1 = p1**2 - d
#             print -p1,(-p1) % abs(m1),(-p1) % abs(m1)
            if (-p1) % abs(m1) ==0:
                x1 = abs(m1)
            else:
                x1 = (-p1) % abs(m1)

            while m1!=1:
                p0 = p1
                q0 = q1
                m0 = m1
                x0 = x1

                p1 = (p0 * x0 +d *q0)/abs(m0)
                q1 = (p0 + x0)/abs(m0)

                m1 = (x0**2 -d)/m0 

                if (-x0)%abs(m1) ==0:
                    x1 = abs(x0)
                else:
                    x1 = (-x0)%abs(m1)
            if p1>x_max:
                x_max = p1
                d_max = d
                print "d= %04d  x = %d"%(d_max,x_max)
    print 

if __name__=='__main__':
    start = time()
    chakravals(1000)
    end = time()
    print "time elapse=%f"%(end - start)

Java程序：

这个跑的好慢的

package project61;
import java.math.*;  

public class P66
{
    public static final int precision = 500;
    public static void main( String args[] )
    {
        BigInteger Max = new BigInteger("0");
        int ans = 0;  

outer:  for (int D_i = 2; D_i <= 1000; D_i++)
        {
            BigDecimal D = new BigDecimal(D_i);
            BigDecimal SD = calculation.Sqrt(D);  

            BigDecimal SD_i = SD.setScale(0, BigDecimal.ROUND_FLOOR);
            if (SD_i.multiply(SD_i).equals(D))
                continue;  

            int a[] = calculation.toContinuedFraction(SD, 100);  

            for (int i = 1; i < 100; i++)
            {
                Fraction temp = new Fraction(a[i],1);  

                for (int j = i - 1; j >= 0; j--)
                    temp = Fraction.Compute(a[j], temp);  

                BigInteger y_2 = temp.denominator.multiply(temp.denominator);
                BigInteger x_2 = temp.numerator.multiply(temp.numerator);
                BigInteger result = x_2.subtract(y_2.multiply(D.toBigIntegerExact())).subtract(BigInteger.ONE);  

                if (result.equals(BigInteger.ZERO))
                {
                    if (temp.numerator.compareTo(Max) > 0)
                    {
                        Max = temp.numerator;
                        ans = D_i;
                    }  

                    continue outer;
                }  

            }
            System.out.print("Warning!\n");  

        }
        System.out.print(ans+"\n");
    }
}  

class Fraction
{
    public BigInteger numerator;
    public BigInteger denominator;  

    private Fraction()
    {  

    }
    public Fraction (int numerator, int denominator)
    {
        this.numerator = BigInteger.valueOf(numerator);
        this.denominator = BigInteger.valueOf(denominator);
    }
    public static Fraction Compute(int p1, Fraction p2)
    {
        Fraction ans = new Fraction();
        ans.numerator = p2.denominator.add(p2.numerator.multiply(BigInteger.valueOf(p1)));
        ans.denominator = p2.numerator.add(BigInteger.ZERO);
        return ans;
    }
}  

class calculation
{
    private static final BigDecimal N0 = new BigDecimal(0);
    private static final BigDecimal N1 = new BigDecimal(1);
    private static final BigDecimal N2 = new BigDecimal(2);  

    public static BigDecimal Sqrt(BigDecimal In)
    {
        BigDecimal N = new BigDecimal(1);
        while(true)
        {
            BigDecimal NN = N.multiply(N);
            NN = NN.add(In);
            NN = NN.divide(N2);
            NN = NN.divide(N, P66.precision, BigDecimal.ROUND_FLOOR);  

            if (NN.equals(N))
                break;  

            N = NN;
        }  

        return N;
    }
    public static int[] toContinuedFraction(BigDecimal In, int l)
    {
        int ans[] = new int[l];  

        BigDecimal temp = In.add(N0);
        for (int i = 0; i < l; i++)
        {
            ans[i] = Integer.valueOf(temp.setScale(0, BigDecimal.ROUND_FLOOR).toString()).intValue();
            temp = temp.subtract(temp.setScale(0, BigDecimal.ROUND_FLOOR));
            temp = N1.divide(temp, P66.precision, BigDecimal.ROUND_FLOOR);
        }
        return ans;
    }
}

最后两个程序在网上复制过来的