sklearn学习笔记之岭回归

岭回归

岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

使用sklearn.linear_model.Ridge进行岭回归

一个简单的例子

from sklearn.linear_model import Ridge
clf = Ridge(alpha=.5)
X = [[0,0],[0,0],[1,1]]
y = [0,.1,1]
clf.fit(X,y)
print(clf.coef_)
print(clf.intercept_)

运行结果如下：

使用方法

实例化

Ridge类已经设置了一系列默认的参数，因此clf = Ridge()即可以完成实例化。

但是，了解一下它的参数还是有必要的：

• alpha：正则化项的系数

• copy_X：是否对X数组进行复制，默认为True，如果选False的话会覆盖原有X数组

• fit_intercept：是否需要计算截距

• max_iter：最大的迭代次数，对于sparse_cg和lsqr而言，默认次数取决于scipy.sparse.linalg，对于sag而言，则默认为1000次。

• normalize：标准化X的开关，默认为False

• solver：在计算过程中选择的解决器

  • auto：自动选择
  • svd：奇异值分解法，比cholesky更适合计算奇异矩阵
  • cholesky：使用标准的scipy.linalg.solve方法
  • sparse_cg：共轭梯度法，scipy.sparse.linalg.cg,适合大数据的计算
  • lsqr：最小二乘法，scipy.sparse.linalg.lsqr
  • sag：随机平均梯度下降法，在大数据下表现良好。

  注：后四个方法都支持稀疏和密集数据，而sag仅在fit_intercept为True时支持密集数据。

• tol：精度

• random_state：sag的伪随机种子

以上就是所有的初始化参数，当然，初始化后还可以通过set_params方法重新进行设定。

回归分析

在实例化Ridge类以后，就可以直接使用Ridge中集成的方法来进行回归了，与绝大多数的sklearn类一样，Ridge使用fit方法执行计算

• fit(X,y,sample\_weight=None)：X是一个array类型，这是特征矩阵，包含着数据集每一条记录的特征值（N*M），y是结果矩阵，同样是array类型，可以是N*1的形状，也可以是N*K的形状,sample_weight代表着权重，可以是一个实数，也可以给每一条记录分配一个值（array类型）。

得到回归函数后，我们可以通过predict来使用回归函数。

• predict(X)：X测试数据集，此方法将返回回归后的结果

对于模型的好坏，Ridge当然提供了评价的方法——score

• score(X,y,sample_weight=None)：X为测试数据，y是测试数据的实际值，类型与fit中的相同，sample是权重

在sklearn中并没有提供直接的查看回归方程的函数，因此查看的时候需要自己转化一下。其实，sklearn就是把相关系数和残差分开保存了，因此，查看的时候要调用coef_和intercept_两个属性。

• coef_：相关系数(array类型)
• intercept_：截距，在fit_intercept=False的时候，将会返回0

可能有用的方法

这些方法在sklearn的基类中就已经集成，但在一般情况下，通常不会用到。

• get_params(deep=True)：这是获取Ridge实例属性取值的方法，可以忽略
• set_params(**params)：与get_params方法相对，是设置属性值，在岭回归中还是比较重要的，毕竟岭回归的alpha值在一开始可能并不知道，需要在一个范围内进行尝试，因此，利用这个方法来设置alpha值还是比较有用的。

以上就是Ridge的总体介绍，在现实生活中，一般不会想上面的实例中的直接使用定值来计算，下面是一个更实际一点的例子：

# Author: Fabian Pedregosa -- <fabian.pedregosa@inria.fr>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

###############################################################################
# Compute paths

n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)

coefs = []
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(X, y)
    coefs.append(clf.coef_)

###############################################################################
# Display results

ax = plt.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
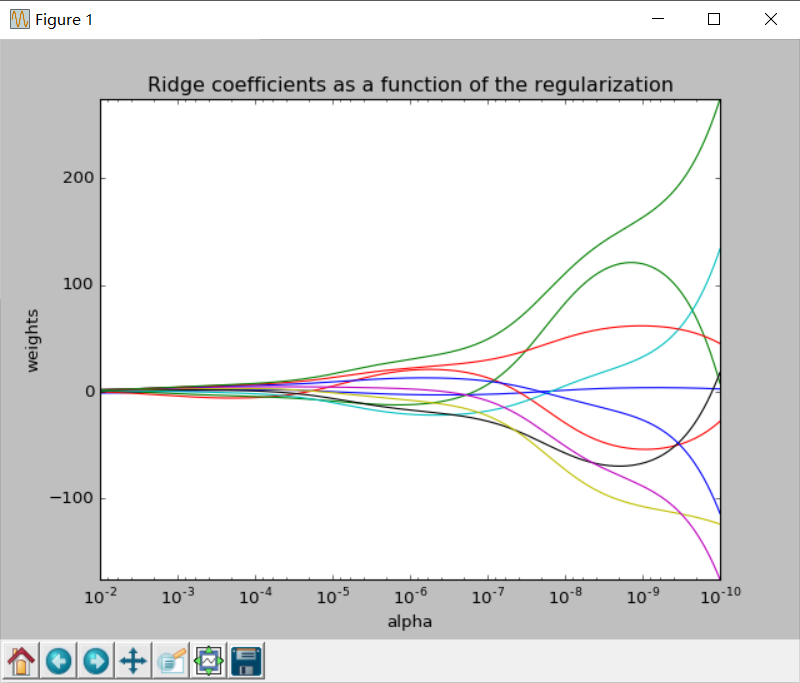
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

这个例子中，alpha为1e-10~1e-2，以对数值等分，对每一个aplha进行一次计算，最后画出岭迹图。岭迹图的样子如下：

到此，岭回归的内容就结束了，我是sklearn的小小搬运工^_^/