HDU 3467 Song of the Siren（圆交）

Problem Description

In the unimaginable popular DotA game, a hero Naga Siren, also known as Slithice, has a very powerful skill: Song of the Siren, Slithice’s charming song draws all of the nearby enemies into deep sleep.

Now iSea meet a group of very powerful opponent, he needs to use this skill to draw all of the enemy's five heroes into hypnosis, and only finishing this leaves the chance to win for him. If we have already got the coordinates of the opponents, in where can Slithice sing the song to hypnotize all the opponents?

 

Input

There are several test cases in the input.

Each test case begin with an integer R (1 ≤ R ≤ 1000), indicating the range of the song, all heroes are hypnotized if the distance between Slithice is no larger than R.
The following line contains ten integers, indicating the coordinates of the five opponents, and -10000 ≤ x, y ≤ 10000.

The input terminates by end of file marker.

Output

For each test case, output one line:
If no such point, output "Poor iSea, maybe 2012 is coming!"
If only one such point, output "Only the point (x, y) is for victory." (x, y) that the only point Slithice can sing.
If there are plenty of such points, output "The total possible area is X." X indicating the total area Slithice can sing.
All the floating numbers should be rounded to two fractional digits.

 

题目大意：给5个点，问是否存在一个点，使得这个点在半径R内包含这5个点，若只存在一个点则输出这个点，存在多个则输出这个点集的面积。

思路：参考http://hi.baidu.com/aekdycoin/item/7618bee9f473ed3e86d9ded6

据说此题可以各种水……

关于集合求交的部分，本人选择了一边求一个新的集合一边和旧的集合合并的方法（都先存起来最后合并的话不知道怎么分辨哪些是同一个集合的，不知道有木有什么高端的姿势？)，不过集合的数量最多应该不会超过2（单从代码上看是这样）。

复杂度O(n^2)

 

代码（15MS）：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 using namespace std;

 const double PI = acos(-1.0);
 const double EPS = 1e-;

 double Deg2Rad(double deg){return (deg * PI / 180.0);}
 double Rad2Deg(double rad){return (rad * 180.0 / PI);}
 double Sin(double deg){return sin(Deg2Rad(deg));}
 double Cos(double deg){return cos(Deg2Rad(deg));}
 double ArcSin(double val){return Rad2Deg(asin(val));}
 double ArcCos(double val){return Rad2Deg(acos(val));}
 double Sqrt(double val){return sqrt(val);}

 inline int sgn(double x) {
     return (x > EPS) - (x < -EPS);
 }

 inline double sqr(double x) {
     return x * x;
 }

 struct Point {
     double x, y;
     Point() {}
     Point(double x, double y): x(x), y(y) {}
     void read() {
         scanf("%lf%lf", &x, &y);
     }
     double length() const {
         return sqrt(x * x + y * y);
     }
     Point operator + (const Point &rhs) const {
         return Point(x + rhs.x, y + rhs.y);
     }
     Point operator - (const Point &rhs) const {
         return Point(x - rhs.x, y - rhs.y);
     }
     Point operator * (double t) const {
         return Point(x * t, y * t);
     }
     Point operator / (double t) const {
         return Point(x / t, y / t);
     }
     Point unit() const {
         double l = length();
         return *this / l;
     }
     double angle() const {
         return atan2(y, x);
     }
 };

 double dist(const Point &a, const Point &b) {
     return (a - b).length();
 }

 Point rotate(const Point &p, double angle, const Point &o = Point(, )) {
     Point t = p - o;
     double x = t.x * cos(angle) - t.y * sin(angle);
     double y = t.y * cos(angle) + t.x * sin(angle);
     return Point(x, y) + o;
 }

 double cross(const Point &a, const Point &b) {
     return a.x * b.y - a.y * b.x;
 }

 double cross(const Point &sp, const Point &ep, const Point &op) {
     return cross(sp - op, ep - op);
 }

 struct Region {
     double st, ed;
     Region() {}
     Region(double st, double ed): st(st), ed(ed) {}
 };

 struct Circle {
     Point c;
     double r;
     Circle() {}
     Circle(Point c, double r): c(c), r(r) {}
     void read() {
         c.read();
         scanf("%lf", &r);
     }
     double area() const {
         return PI * r * r;
     }
     bool contain(const Circle &rhs) const {
         return sgn(dist(c, rhs.c) + rhs.r - r) <= ;
     }
     bool contain(const Point &p) const {
         return sgn(dist(c, p) - r) <= ;
     }
     bool intersect(const Circle &rhs) const {
         return sgn(dist(c, rhs.c) - r - rhs.r) < ;
     }
     bool tangency(const Circle &rhs) const {
         return sgn(dist(c, rhs.c) - r - rhs.r) == ;
     }
     Point pos(double angle) const {
         Point p = Point(c.x + r, c.y);
         return rotate(p, angle, c);
     }
 };

 void intersection(const Circle &cir1, const Circle &cir2, Point &p1, Point &p2) {
     double l = dist(cir1.c, cir2.c);
     double d = (sqr(l) - sqr(cir2.r) + sqr(cir1.r)) / ( * l);
     double d2 = sqrt(sqr(cir1.r) - sqr(d));
     Point mid = cir1.c + (cir2.c - cir1.c).unit() * d;
     Point v = rotate(cir2.c - cir1.c, PI / ).unit() * d2;
     p1 = mid + v, p2 = mid - v;
 }

 const int MAXN = ;

 struct Region_vector {
     int n;
     Region v[];
     void clear() {
         n = ;
     }
     void add(const Region &r) {
         v[n++] = r;
     }
 } *last, *cur;

 Circle cir[MAXN];
 bool del[MAXN];
 double r;
 int n = ;

 double CommonArea(const Circle &A, const Circle &B) {
     double area = 0.0;
     const Circle & M = (A.r > B.r) ? A : B;
     const Circle & N = (A.r > B.r) ? B : A;
     double D = dist(M.c, N.c);
     if((D < M.r + N.r) && (D > M.r - N.r)) {
         double cosM = (M.r * M.r + D * D - N.r * N.r) / (2.0 * M.r * D);
         double cosN = (N.r * N.r + D * D - M.r * M.r) / (2.0 * N.r * D);
         double alpha = 2.0 * ArcCos(cosM);
         double beta = 2.0 * ArcCos(cosN);
         double TM = 0.5 * M.r * M.r * Sin(alpha);
         double TN = 0.5 * N.r * N.r * Sin(beta);
         double FM = (alpha / 360.0) * M.area();
         double FN = (beta / 360.0) * N.area();
         area = FM + FN - TM - TN;
     }
     else if(D <= M.r - N.r) {
         area = N.area();
     }
     return area;
 }

 bool isOnlyOnePoint() {
     bool flag = false;
     Point t;
     for(int i = ; i < n; ++i)
         for(int j = i + ; j < n; ++j) {
             if(cir[i].tangency(cir[j])) {
                 flag = true;
                 t = (cir[i].c + cir[j].c) / ;
                 break;
             }
         }
     if(!flag) return false;
     for(int i = ; i < n; ++i)
         if(!cir[i].contain(t)) return false;
     printf("Only the point (%.2f, %.2f) is for victory.\n", t.x + EPS, t.y + EPS);
     return true;
 }

 bool solve() {
     if(isOnlyOnePoint()) return true;
     memset(del, , sizeof(del));
     for(int i = ; i < n; ++i)
         for(int j = ; j < n; ++j) {
             if(del[j] || i == j) continue;
             if(cir[i].contain(cir[j])) {
                 del[i] = true;
                 break;
             }
         }
     double ans = ;
     for(int i = ; i < n; ++i) {
         if(del[i]) continue;
         last->clear();
         Point p1, p2;
         for(int j = ; j < n; ++j) {
             if(del[j] || i == j) continue;
             if(!cir[i].intersect(cir[j])) return false;
             cur->clear();
             intersection(cir[i], cir[j], p1, p2);
             double rs = (p2 - cir[i].c).angle(), rt = (p1 - cir[i].c).angle();
             if(sgn(rs) < ) rs +=  * PI;
             if(sgn(rt) < ) rt +=  * PI;
             if(last->n == ) {
                 if(sgn(rt - rs) < ) cur->add(Region(rs,  * PI)), cur->add(Region(, rt));
                 else cur->add(Region(rs, rt));
             } else {
                 for(int k = ; k < last->n; ++k) {
                     if(sgn(rt - rs) < ) {
                         if(sgn(last->v[k].st - rt) >=  && sgn(rs - last->v[k].ed) >= ) continue;
                         if(sgn(last->v[k].st - rt) < ) cur->add(Region(last->v[k].st, min(last->v[k].ed, rt)));
                         if(sgn(rs - last->v[k].ed) < ) cur->add(Region(max(last->v[k].st, rs), last->v[k].ed));
                     } else {
                         if(sgn(rt - last->v[k].st) <=  || sgn(last->v[k].ed - rs) <= ) continue;
                         cur->add(Region(max(rs, last->v[k].st), min(rt, last->v[k].ed)));
                     }
                 }
             }
             swap(last, cur);
             if(last->n == ) break;
         }
         for(int j = ; j < last->n; ++j) {
             p1 = cir[i].pos(last->v[j].st);
             p2 = cir[i].pos(last->v[j].ed);
             ans += cross(p1, p2) / ;
             double angle = last->v[j].ed - last->v[j].st;
             ans += 0.5 * sqr(cir[i].r) * (angle - sin(angle));
         }
     }
     if(sgn(ans) == ) return false;
     printf("The total possible area is %.2f.\n", ans + EPS);
     //printf("%.2f\n", CommonArea(cir[0], cir[4]));
     return true;
 }

 int main() {
     last = new Region_vector, cur = new Region_vector;
     while(scanf("%lf", &r) != EOF) {
         Point t;
         for(int i = ; i < n; ++i) {
             t.read();
             cir[i] = Circle(t, r);
         }
         if(!solve()) puts("Poor iSea, maybe 2012 is coming!");
     }
 }

---

以下转自：http://hi.baidu.com/aekdycoin/item/7618bee9f473ed3e86d9ded6

【问题求解】
给定N 个圆形，求出其交集.

【算法分析】

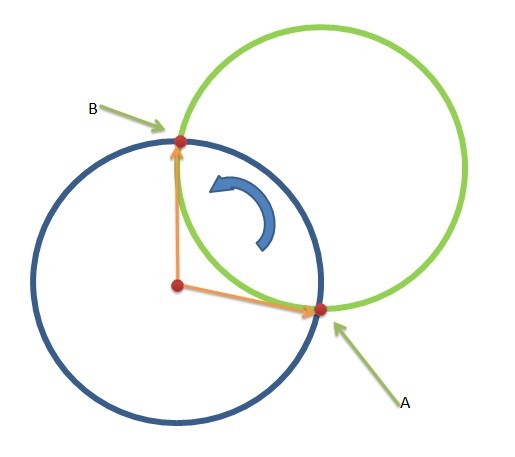
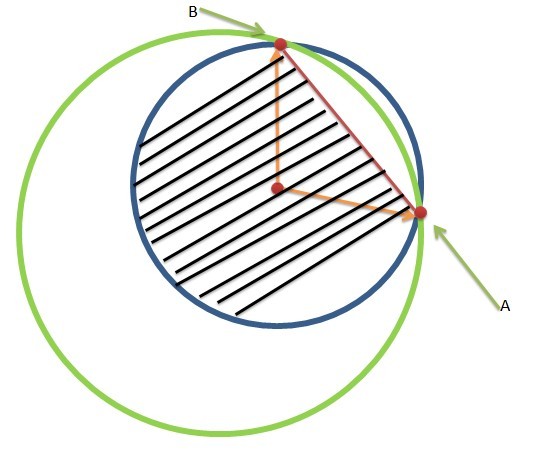
考虑上图中的蓝色圆,绿色的圆和蓝色的圆交于 A,B 2个交点 ,我们在逆时针系下考虑，那么 可以知道 对于蓝色的圆，它对应的某个 角度区间被覆盖了

假设 区间为 [A, B], 并且角度是按照 圆心到交点的 向量的 极角来定义 (为了方便，我一般都把角度转化到 [0,2pi]区间内) 那么可以知道在这种 标识情况下，可能存在以下情况

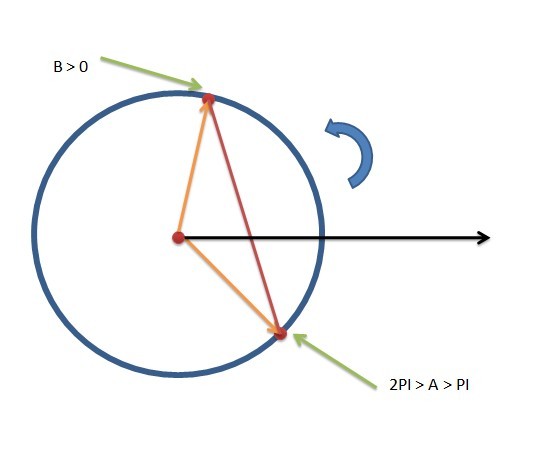
这种区间的跨度如何解决呢?实际上十分简单，只需要把[A,B] 拆成 [A, 2PI], [0,B]即可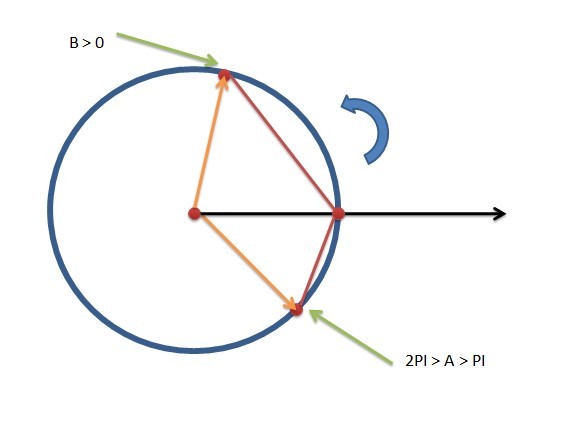

下面介绍一下 对于我们当前所求任务的实际运用( 利用上述做法)

首先 对于所给的N个圆，我们可以进行去冗杂，表现为:
(1) 去掉包含(内含 or 内切)了某些圆的大圆
(2) 去掉相同的圆
(3) 如果存在2个圆不交，则直接返回 0 (交集必然为空)

经过以上几步，可以发现得到的圆都是两两相交的。于是枚举一个圆，并对于剩下的圆和它求交点，对于所求的的交点，可以得到一个角度区间 [A,B], 当然区间如果跨越了(例如 [1.5PI, 0.5PI],注意这里是有方向的) 2PI那么需要拆 区间

可以知道，最后区间的交集必然是最后 所有圆交集的一个边界！

于是我们在得到区间的情况下累积弓形的面积

提示： 在获得区间的过程中可能存在下面的情况，请注意！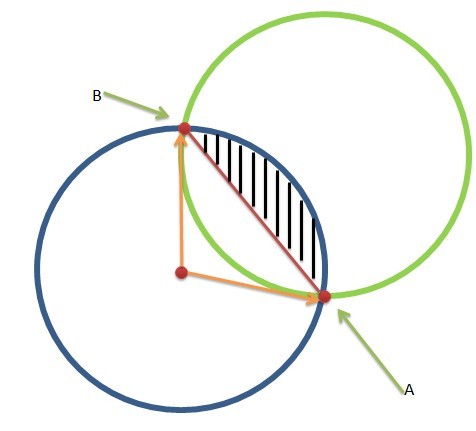

显然包括上面的2个情况，注意使用“归一化”的判断思想来获得区间！ (左图是 [A,B],右图是 [B,A],注意顺序！)

之后把当前的"点" 假如S集合中

最后的答案累加上S的凸包的面积即可(XXXXX)

完全不需要再求一次凸包,获得区间以后就获得了唯一的S凸包中的一条边，那么我们只需要累加他们叉乘的和！ (可以理解为一边保存边一边算面积！,代码长度缩短 10%以上)

枚举圆 O(n)
每一次求交O(n) 
获得的交点区间排序，离散化，求交 O(nlogn)  (至多 O(2* n)个区间)
最后的求凸包 O(nlogn) (交点不会太多，至多2*n)
所以总的复杂度为 O(n^2 log n)

【题目推荐】

http://acm.hdu.edu.cn/showproblem.php?pid=3467
赤裸裸的圆交题目， 显然标程 被CHA ，此题数据比较水 (我至少用4个版本的错误代码AC)
http://acm.hdu.edu.cn/showproblem.php?pid=3239

虽然没有上面那题那么赤裸裸，可是推出模型以后直接用容斥 + 求圆交……

PS.这种做法如果实现的好，那么精度是比较高的！