POJ 1696 Space Ant（凸包变形）

Description

The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations: 

1. It can not turn right due to its special body structure.
2. It leaves a red path while walking.
3. It hates to pass over a previously red colored path, and never does that.

The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y. 
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance. 
The problem is to find a path for an M11 to let it live longest. 
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.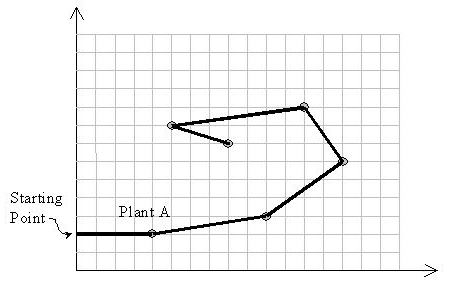 

Input

The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.

Output

Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.

 

题目大意：从与最低点有相同纵坐标的y轴上的点出发，只能左转，问最多走过多少个点，把这些点列出来。

思路：细细斟酌，发现其实全部都能走嘛o(╯□╰)o。

像凸包构造那样走，就能走完了，其实就是一个凸包的变种o(╯□╰)o

数据范围比较小就直接O(n²)暴力算了o(╯□╰)o

 

代码（0MS）：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <cmath>
 using namespace std;

 const double EPS = 1e-;

 inline int sgn(double x) {
     return (x > EPS) - (x < -EPS);
 }

 struct Point {
     double x, y;
     Point() {}
     Point(double x, double y): x(x), y(y) {}
     void read() {
         scanf("%lf%lf", &x, &y);
     }
     bool operator < (const Point &rhs) const {
         if(y != rhs.y) return y < rhs.y;
         return x < rhs.x;
     }
     Point operator + (const Point &rhs) const {
         return Point(x + rhs.x, y + rhs.y);
     }
     Point operator - (const Point &rhs) const {
         return Point(x - rhs.x, y - rhs.y);
     }
     Point operator * (const int &b) const {
         return Point(x * b, y * b);
     }
     Point operator / (const int &b) const {
         return Point(x / b, y / b);
     }
     double length() const {
         return sqrt(x * x + y * y);
     }
     Point unit() const {
         return *this / length();
     }
 };
 typedef Point Vector;

 double dist(const Point &a, const Point &b) {
     return (a - b).length();
 }

 double across(const Point &a, const Point &b) {
     return a.x * b.y - a.y * b.x;
 }
 //turn left
 bool cross(const Point &sp, const Point &ed, const Point &op) {
     return sgn(across(sp - op, ed - op)) > ;
 }

 /*******************************************************************************************/

 const int MAXN = ;

 Point p[MAXN];
 bool del[MAXN];
 int n, T;

 void solve() {
     memset(del, , sizeof(del));
     int last = ;
     for(int i = ; i < n; ++i)
         if(p[i] < p[last]) last = i;
     for(int i = ; i < n; ++i) {
         printf(" %d", last + );
         del[last] = true;
         int t = ;
         for(t = ; t < n; ++t) if(!del[t]) break;
         for(int j = ; j < n; ++j) {
             if(del[j] || j == t) continue;
             if(cross(p[j], p[t], p[last])) t = j;
         }
         last = t;
     }
 }

 int main() {
     scanf("%d", &T);
     while(T--) {
         scanf("%d", &n);
         int t;
         for(int i = ; i < n; ++i)
             scanf("%d", &t), p[i].read();
         printf("%d", n);
         solve();
         puts("");
     }
 }