[递推+矩阵快速幂]Codeforces 1117D - Magic Gems

传送门：Educational Codeforces Round 60 – D

 

题意：

给定N，M（n <1e18,m <= 100）

一个magic gem可以分裂成M个普通的gem，现在需要N个gem，可以选择一定的magic gem，指定每一个分裂或不分裂，问一共有多少种方案

两种分裂方案不同当且仅当magic gem的数量不同，或者分裂的magic gem的索引不同。

思路：

1.首先从dp的角度出发

设F(i)为最终需要i个gem的方案数，容易得到递推式：

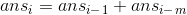
(总方案数 = 最右边的magic gem分裂得到的方案数 + 最右边的magic gem不分裂得到的方案数）

2.观察数据范围可以看到，如果直接这样计算，时间复杂度是要上天的

我们可以把递推式求解转化成矩阵乘法求解

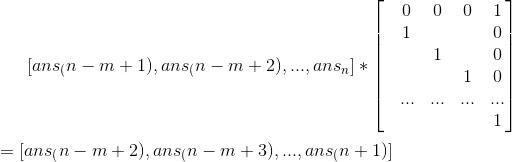
3.套用矩阵快速幂的板子，加速计算

参考代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define _____ ios::sync_with_stdio(false);cin.tie(0);
const int M = 1e9 + ;
//head

ll n,m;
struct Mat{
    ll a[][];
};
Mat mul(const Mat & a,const Mat & b){
    Mat ans;
    for(int i = ; i <= m; i++){
        for(int j = ; j <= m; j++){
            ans.a[i][j] = ;
            for(int k = ; k <= m; k++){
                ans.a[i][j] += a.a[i][k]*b.a[k][j];
                if(ans.a[i][j] > M)ans.a[i][j] %= M;
            }
        }
    }
    return ans;
}
Mat quick_pow(Mat a,ll b){
    Mat t;
    for(int i = ; i <= m; i++)t.a[i][i] = ;
    while(b){
        if(b & )t = mul(t,a);
        b >>= ;
        a = mul(a,a);
    }
    return t;
}
int main(){
    //freopen("data.in","r",stdin);
    _____
    cin >> n >> m;
    if(n < m){cout <<  << '\n';}
    else{
        Mat ans,t;
        for(int i = ; i < m; i++){
            ans.a[i+][i] = ;
        }
        ans.a[][m] = ans.a[m][m] = ;
        ans = quick_pow(ans,n-m);
        Mat a;
        for(int i = ; i < m; i++)a.a[][i] = ;
        a.a[][m] = ;
        a = mul(a,ans);
        cout << a.a[][m] << '\n';
    }
    return ;
}