组合数学_第4章_Polya定理

第4章 Polya定理

4.1 群的概念

4.1.1 群的定义

给定一个集合\(G=\{a,b,c,\cdots\}\)和集合\(G\)上的二元运算“\(\cdot\)”，并满足下列4个条件：

1. 封闭性：若\(a,b \in G\)，则存在\(c \in G\)，使得，

   \[a \cdot b=c
   \]

2. 结合律：对于任意的\(a,b,c \in G\)，恒有

   \[(a \cdot b) \cdot c = a \cdot (b \cdot c)
   \]

3. 存在单位元素：\(G\)中存在一个元素\(e\)，使得对于\(G\)的任意元素\(a\)，恒有

   \[a \cdot e = e \cdot a = a
   \]

4. 存在逆元素：对于\(G\)的任意元素\(a\)，恒有一个\(b \in G\)，使得

   \[a \cdot b = b \cdot a = e
   \]

   元素\(b\)称为元素\(a\)的逆元素，记作\(a^{-1}\)，即

   \[b= a^{-1}
   \]

则称集合\(G\)在运算\(\cdot\)之下是一个群，有时也称\(G\)是一个群，\(G\)中元素\(a\)对\(b\)的运算\(a \cdot b\)，可以简记为\(ab\)。

---

例题：\(G=\{1,-1\}\)在乘法运算下是一个群。

解：（1）封闭性：(1)(-1)=-1,(1)(1)=1,(-1)(1)=-1,(-1)(-1)=1

（2）结合性：显然

（3）单位元素：\(e=1\)

（4）逆元素：由于(1)(1)=1,(-1)(-1)=1，故\((-1)^{-1}=-1,(1)^{-1}=1\)

---

群的元素个数是有限的，称为有限群。有限群\(G\)的元素个数叫做群的阶，记为\(|G|\)。当群的元素为无限时，称为无限群。

若群\(G\)的任意二元素\(a,b\)恒满足\(ab=ba\)时，称\(G\)为交换群或Abel群。

4.1.2 群的性质

1. 群的单位元是唯一的。
2. \(ab=ac \Rightarrow b=c,ba=ca \Rightarrow b=c\)
3. \(G\)中每一个元素的逆元素是唯一的。
4. \((abc \cdots lmn)^{-1}=n^{-1}m^{-1}l^{-1} \cdots c^{-1}b^{-1}a^{-1}\)
5. …

设\(G\)是群，\(H\)是\(G\)的子集，若\(H\)在\(G\)的原来定义的运算下也成群，则称\(H\)是\(G\)的子群。

4.2 置换群

置换群是十分重要的群，特别是所有的有限群都可以用它来表示。

不失一般性，假定\(n\)个元素为\(1,2,...,n\)。若元素\(1\)被\(1\)到\(n\)中某一整数\(a_1\)所取代，\(2\)被其中的\(a_2\)元素所取代，…，\(n\)被\(a_n\)所取代，且

\[a_i \neq a_j，若i \neq j，i,j \neq 1,2,\cdots,n
\]

用

\[p =\begin{pmatrix} 1 & 2 & 3 & \cdots & n \\ a_1 & a_2 & a_3 & \cdots & a_n \end{pmatrix}\\
\]

来表示。

置换群的定义为：设

\[p_1 =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}, p_2 =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix}
\]

\[p_1p_2
=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix} \\
=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}\begin{pmatrix} 3 & 1 & 2 & 4 \\ 2 & 4 & 3 & 1 \end{pmatrix} \\
=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 3 & 1 \end{pmatrix}
\]

先做\(p_1\)的置换，再作\(p_2\)的置换：

\[1 \stackrel{p_1} {\longrightarrow} 3 \stackrel{p_2} {\longrightarrow} 2 \\
2 \stackrel{p_1} {\longrightarrow} 1 \stackrel{p_2} {\longrightarrow} 4 \\
3 \stackrel{p_1} {\longrightarrow} 2 \stackrel{p_2} {\longrightarrow} 3 \\
4 \stackrel{p_1} {\longrightarrow} 4 \stackrel{p_2} {\longrightarrow} 1 \\
\]

简单来说就是先经过了\(p_1\)的映射再经过了\(p_2\)的映射。

循环节数：

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 5 & 1 & 4 & 2 \end{pmatrix}=(13)(25)(4)
\]

1置换为3，同时3又能置换为1，这就是一个循环。4置换为4本身，这也算一个循环。左右两个表示是等价的，从后面的表示可以清楚的看到每个循环，以及循环节的个数。

4.3 Polya定理

设\(\overline{G}\)是\(n\)个对象的一个置换群，用\(m\)种颜色涂染这\(n\)个对象，则不同染色的方案数为

\[l=\frac{1}{|\overline{G}|}[m^{c(\overline{a_1})}+m^{c(\overline{a_2})}+\cdots+m^{c(\overline{a_g})}]
\]

其中，\(\overline{G}=\{\overline{a_1},\overline{a_2},\cdots,\overline{a_g}\}\)，\(c(\overline{a_k})\)为置换\(\overline{a_k}\)的循环节数。

\(n\)个对象可用\(1,2,...,n\)编号，故\(\overline{G}\)可当作\((1,2,\cdots,n)\)的一个置换群。

---

例题：用2种颜色去染排成一个环的6个棋子，如果通过旋转得到则只算一种，一共有多少种染色方案？

解：典型的满足polya公式的条件，\(m=2\)，\(n=6\)。因为是旋转得到的置换，所以存在6个置换（自己置换到自己也算）。

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 4 & 5 & 6 & 1 \end{pmatrix}=(123456)
\]

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 3 & 4 & 5 & 6 & 1 & 2 \end{pmatrix}=(135)(246)
\]

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 4 & 5 & 6 & 1 & 2 & 3\end{pmatrix}=(14)(25)(36)
\]

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 5 & 6 & 1 & 2 & 3 & 4 \end{pmatrix}=(153)(246)
\]

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 6 & 1 & 2 & 3 & 4 & 5\end{pmatrix}=(165432)
\]

\[\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 1 & 2 & 3 & 4 & 5 & 6\end{pmatrix}=(1)(2)(3)(4)(5)(6)
\]

每个置换的循环节已经标出了。所以根据polya定理公式可以算出，染色方案数为\(\frac{1}{6}(2^1+2^2+2^3+2^2+2^1+2^6)=14\)。

---

例题：一个3×3的方格，用10种颜色给每个格子染色，旋转0度、90度、180度、270度后相同的算成相同，问总共有多少种方案？

解：

1. 旋转0度：(1)(2)(3)(4)(5)(6)(7)(8)(9)
2. 旋转90度：(3179)(6248)(5)
3. 旋转180度：(19)(28)(37)(46)(5)
4. 旋转270度：(7931)(4862)(5)

所以根据Polya定理，总方案数就是\(\frac{1}{4}(10^9+10^3+10^5+10^3)\)。

例题：正六面体的6个面分别用红蓝两种颜色着色，问有多少种方案？

解：使正六面体重合的刚体运动群，有如下几种情况：

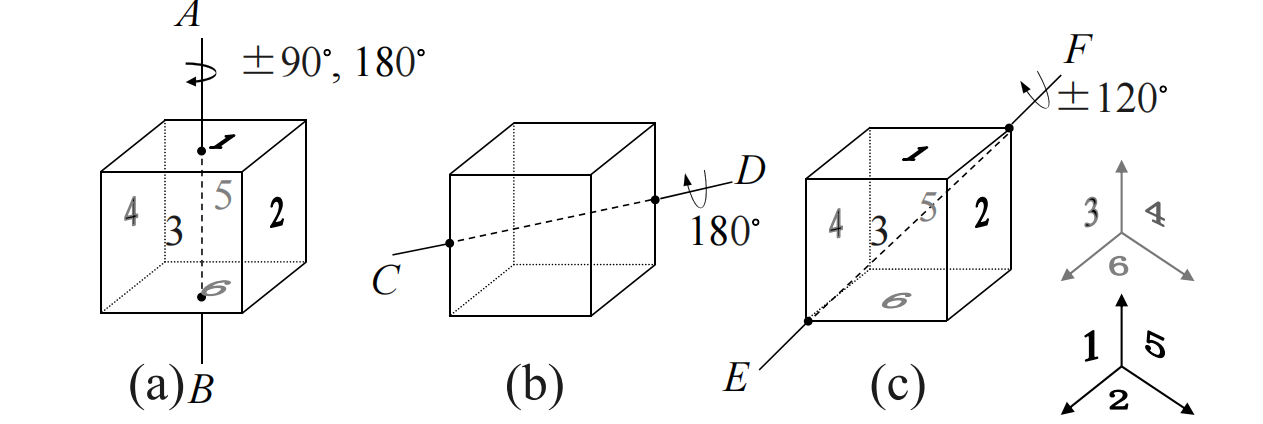
1. 不动置换(1)(2)(3)(4)(5)(6)，格式为\((1)^6\)，只有1种。
2. 绕过面1-面6中心的AB轴旋转90度，对应有(1)(2345)(6)，旋转-90度，对应有(1)(5432)(6)，格式为\((1)^2(4)^1\)，正六面体有3个对面，故同类的置换有6个。
3. 绕AB轴旋转180度，对应有(1)(24)(35)(6)，格式为\((1)^2(2)^2\)，同类置换有3个。
4. 绕CD轴（棱中-棱中）旋转180度的置换为(16)(25)(34)，格式为\((2)^3\)，正六面体中对角线位置的平行的棱有6对，故同类的置换有6个。
5. 绕正六面体的对角线EF（顶点-顶点）旋转120度，对应有(346)(152)，旋转-120度，对应有(643)(251)，格式为\((3)^2\)，正六面体的对角线有4条，故同类的置换有8个。

根据polya定理，不同的颜色方案为

\[M=\frac{1}{24}(2^6+6\cdot2^3+3\cdot2^4+6\cdot2^3+8\cdot2^2) \\
=\frac{1}{24}(64+48+48+48+32) = 10
\]

一种简单的推广：用\(m\)种颜色对正六面体的6个面着色可得不同的方案数\(M\)，根据polya定理，

\[M=\frac{1}{24}(m^6 + 6 \cdot m^3 + 3 \cdot m^4 + 6 \cdot m^3 + 8 \cdot m^2)
\]

---

例题：用2种颜色给正6面体的8个顶点着色，有多少种方案？

解：

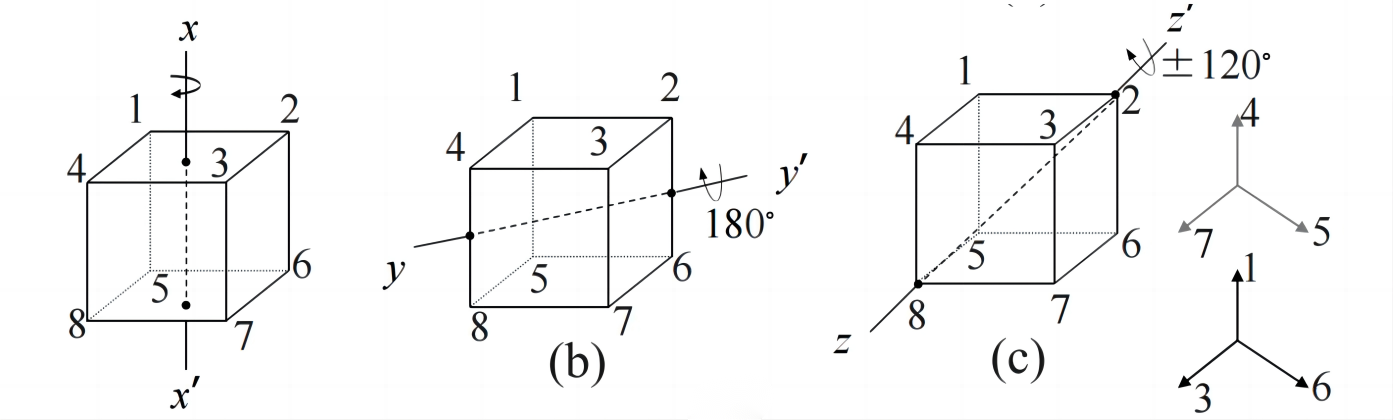
1. 不动置换(1)(2)(3)(4)(5)(6)(7)(8)，格式为\((1)^8\)，只有1种。
2. 绕x轴，旋转90度的置换为(1234)(5678)，旋转-90度的置换为(4321)(8765)，格式为\((4)^2\)，正六面体对面有3对，故同类置换有6个。
3. 绕x轴，旋转180度的置换为(13)(24)(57)(68)，格式为\((2)^4\)，正六面体对面有3对，故同类置换有3个。
4. 绕y轴，旋转180度的置换为(17)(35)(28)(46)，格式为\((2)^4\)，正六面体有12条棱，6对棱，故同类置换有6个。
5. 绕z轴，旋转120度的置换为(136)(2)(457)(8)，旋转-120度的置换为(631)(754)，格式为\((3)^2\)，正六面体有4条对角线，故同类置换为8个。

根据polya定理，不同的着色方案为，

\[M=\frac{1}{24}(2^8 + 6 \cdot 2^2 + 3 \cdot 2^4 + 6 \cdot 2^4 + 8 \cdot 2^4) \\
=\frac{1}{24}(256+24+48+96+128)=\frac{552}{24}=23
\]

例题：一个正6面体的6个面用g，r, b, y四种颜色涂染，求其中两个面用色g，两个面用色y, 其余一面用b, 一面用r的方案数。

解：再次看这个图

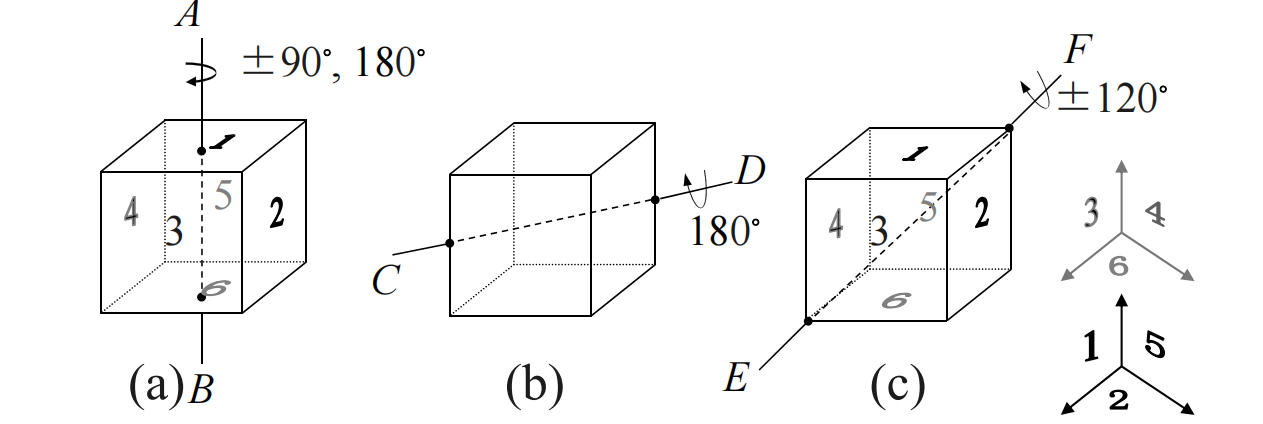
分类讨论	旋转方式	置换群	格式	同类置换个数
1	不动置换	(1)(2)(3)(4)(5)(6)	\((1)^6\)	1
2	绕AB旋转90度和-90度	(1)(2345)(6)和(1)(5432)(6)	\((1)^2(4)\)	2×3=6
3	绕AB旋转180度	(1)(24)(35)(6)	\((1)^2(2)^2\)	3
4	绕CD旋转180度	(16)(34)(25)	\((2)^3\)	6
5	绕EF旋转120度和-120度	(125)(346)和(521)(643)	\((3)^2\)	2×4=8

由母函数形式的polya定理可得

\[L=\frac{1}{24}[(g+r+b+y)^6+6(g+r+b+y)^2(g^4+r^4+b^4+y^4)+3(g+r+b+y)^2(g^2+r^2+b^2+y^2)^2+6(g^2+r^2+b^2+y^2)^3+8(g^3+r^3+b^3+y^3)^2]
\]

所求方案数即\(g^2rby^2\)的系数，故方案数为

\[\frac{1}{24}(C_6^2C_4^2C_2^1C_1^1+3C_2^1C_1^1C_2^1C_1^1)=\frac{192}{24}=8
\]

---

例题：一个正八面体，用红蓝两色对6个顶点进行着色；用黄绿两种颜色对八个面进行染色，试求其中4个顶点为红色，两个顶点为蓝色，黄和绿的面各四面的方案数。

解：

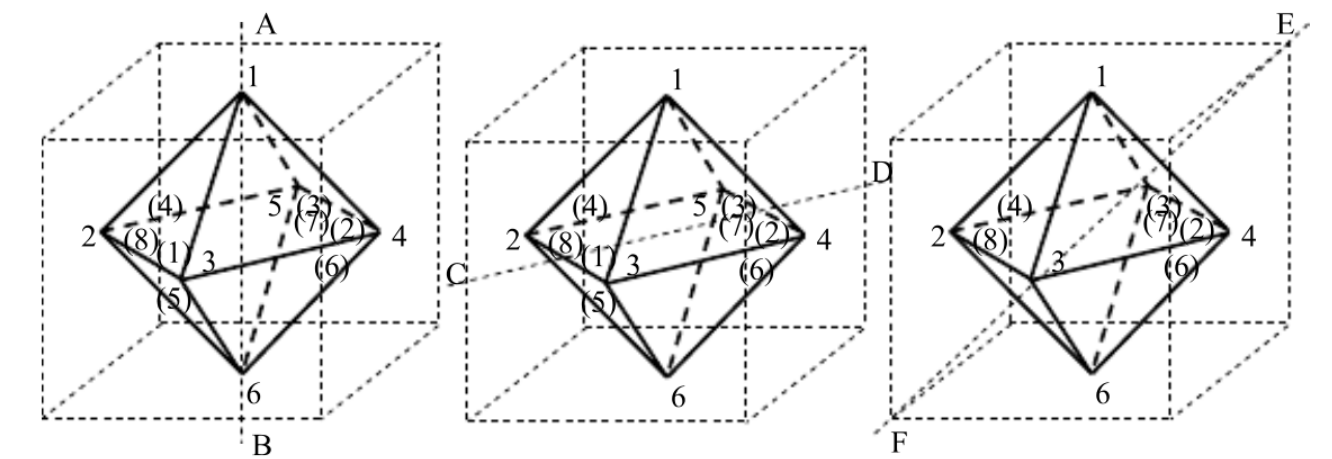
分类讨论	旋转方式	格式	同类置换个数
1	不动置换	\((1)^6\)-\((1)^8\)	1
2	绕AB旋转90度和-90度	\((1)^2(4)\)-\((4)^2\)	2×3=6
3	绕AB旋转180度	\((1)^2(2)^2\)-\((2)^4\)	3
4	绕CD旋转180度	\((2)^3\)-\((2)^4\)	6
5	绕EF旋转120度和-120度	\((3)^2\)-\((1)^2(3)^2\)	2×4=8

根据母函数形式的polya定理，染色方案枚举：

\[P(r,b,y,g)=\frac{1}{24}[(r+b)^6(y+g)^8+6(r+b)^2(r^4+b^4)(y^4+g^4)^2+3(r+b)^2(r^2+b^2)^2(y^2+g^2)^4+6(r^2+b^2)^3(y^2+g^2)^4+8(r^3+b^3)^2(y+g)^2(y^3+g^3)^2]
\]

其中\(r^4b^2y^4g^4\)的系数即为所求方案数：

\[\frac{1}{24}[C_6^4C_2^2C_8^4C_4^4+6\cdot C_2^2C_1^1C_2^1C_1^1+3\cdot(C_2^2C_2^1+C_2^2C_2^2)C_4^2C_2^2+6\cdot C_3^2C_1^1C_4^2C_2^2+8\cdot0]
=\frac{1}{24}[15\times70+6\times2+3\times(2+1)\times6+6\times3\times6+0]
=\frac{1}{24}(1024+12+54+108)
=\frac{1224}{24}
=51
\]

参考资料

• 普通涂色问题 组合数学-Polya定理_ojshilu的博客-CSDN博客_polya定理染色
• Burnside引理和Polya定理 - _努力努力再努力x - 博客园 (cnblogs.com)