胃食管反流之 SAP分析( in the Ohmega software)
原文:https://note.youdao.com/s/GED6wise
SAP analysis in the Ohmega software

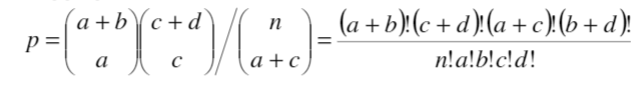

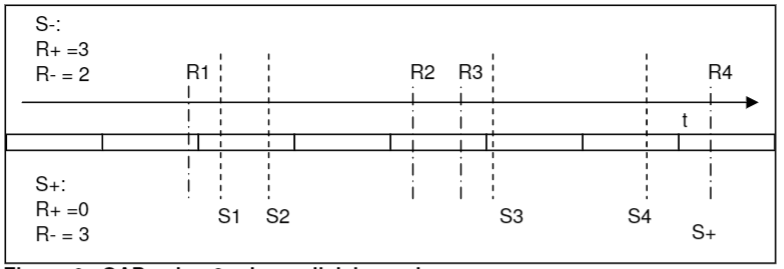
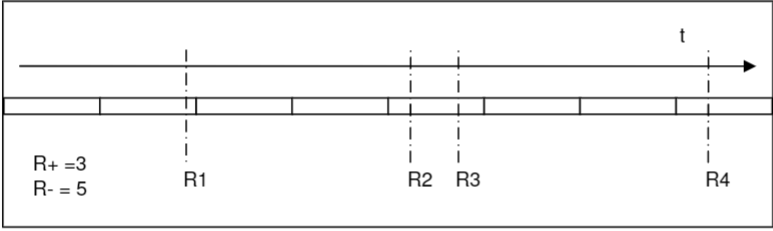
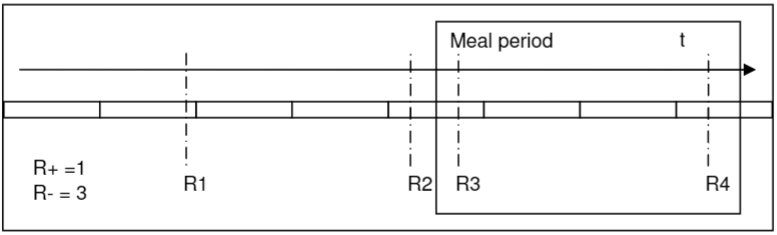
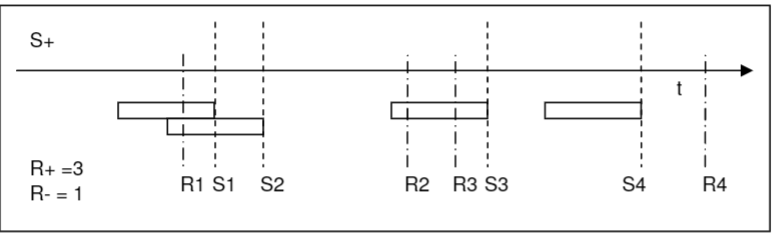
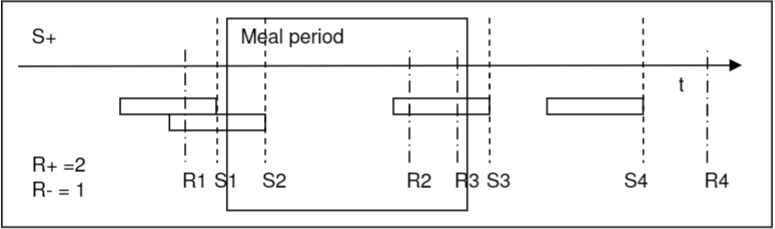
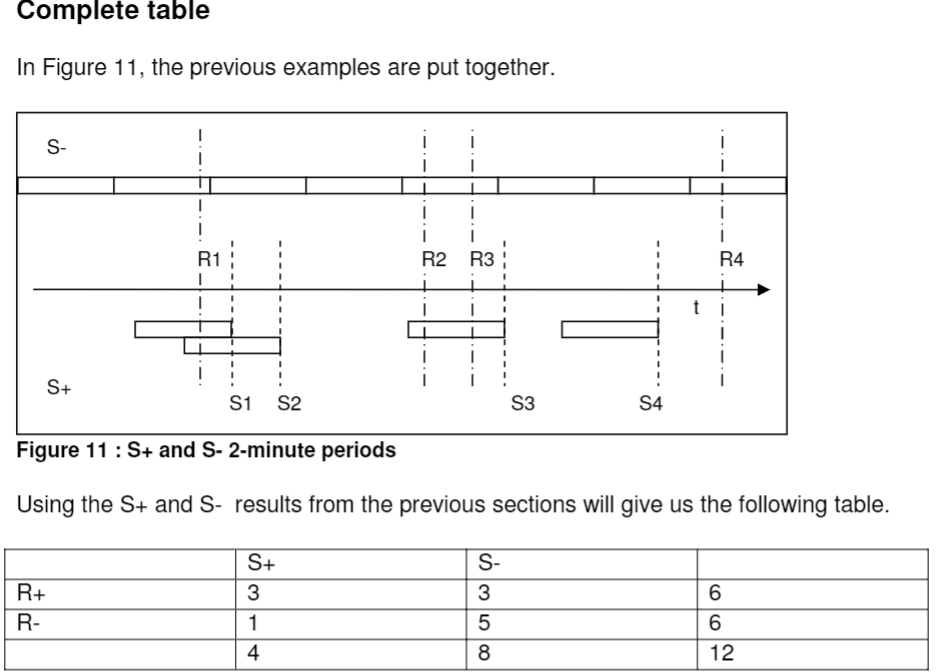

胃食管反流之 SAP分析( in the Ohmega software)的更多相关文章
- SAP分析云及协同计划
大家好, 我是SAP成都研究院S/4HANA Sales 团队的软件工程师Derek.四年前我从SAP Consulting团队转到SAP Labs从事Sales Analytics相关应用的开发,在 ...
- 美国top200药品2
python机器学习-乳腺癌细胞挖掘(博主亲自录制视频)https://study.163.com/course/introduction.htm?courseId=1005269003&u ...
- Configuring SSL for SAP Host Agent on UNIX
https://help.sap.com/viewer/141cbf7f183242b0ad0964a5195b24e7/114/en-US/8d12f7b9244b44219bd14d619d3a2 ...
- Business Process and SAP ERP
1. Definition of Organisation - Organizations are created entities within and through which people i ...
- SAP标准培训课程C4C10学习笔记(一)第一单元
C4C10:SAP Hybris Cloud for Customer Administration 课程目录: 第一单元是C4C的简介. 作为SAP推出的一个SaaS(Software as a s ...
- Redhat下安装SAP的相关
Red Hat Enterprise Linux 6.x: Installation and Upgrade - SAP Note 1496410 Red Hat Enterprise Linux 7 ...
- SAP成都研究院李三郎:SCP Application Router简介
今天的文章来自李贝宁(Ben),SAP成都研究院的资深程序猿和架构师. 作为成都研究院里同时精通Java, JavaScript和ABAP这三门编程语言的数位同事之一,Ben曾经先后担任了成都CRM ...
- ERP_Oracle Erp发展趋势基于SOA电子商务方案
2014-01-12 Created By BaoXinjian
- PA教材提纲 TAW10-1
Unit1 SAP systems(SAP系统) 1.1 Explain the Key Capabilities of SAP NetWeaver(解释SAP NetWeaver的关键能力) Rep ...
- 第二次作业——个人项目实战(Sudoku)
Github:Sudoku 项目相关要求 利用程序随机构造出N个已解答的数独棋盘 . 输入 数独棋盘题目个数N 输出 随机生成N个 不重复 的 已解答完毕的 数独棋盘,并输出到sudoku.txt中, ...
随机推荐
- Unity 音乐或者视频播放完毕之后执行方法
视频播放完毕后,执行某个方法 方法1 官方给的解释 private VideoPlayer video2; private void Awake() { video2.loopPointReached ...
- 20个Python 正则表达式应用与技巧
本文分享自华为云社区<Python 正则表达式大揭秘应用与技巧全解析>,作者:柠檬味拥抱. Python 中的 re 模块是用于处理正则表达式的强大工具.正则表达式是一种用来匹配字符串的模 ...
- 【直播预告】HarmonyOS极客松赋能直播第四期:HarmonyOS开发经验分享
- mysql 必知必会整理—触发器[十五]
前言 现在很多都是程序用于触发的,而不是触发器了. 正文 需要MySQL 5 对触发器的支持是在MySQL 5中增加的.因此,本章内容适用于MySQL 5或之后的版本. MySQL语句在需要时被执行, ...
- React中类组件和函数组件
一.类组件 类组件,顾名思义,也就是通过使用ES6类的编写形式去编写组件,该类必须继承React.Component 如果想要访问父组件传递过来的参数,可通过this.props的方式去访问 在组件中 ...
- 试题B:小球反弹(第十五届蓝桥杯省赛B组c/c++组)
试题B:小球反弹 我在刷博客的时候看见有人分享了蓝桥杯的题目,我想起了我之前大学打蓝桥杯刷题的时光,还是很怀念当时打比赛的氛围,关于这个小球反弹的题目,我感觉很有意思,我一开始也是走了好多弯路,然后去 ...
- 【NOIP2013模拟联考8】匹配(match) 题解
B 组都说看不懂--我也解释不清啊--只能写这么详细了 其实就是道板题 省流:f[i][s][j]表示字符串长度i,匹配情况s,ac自动机节点j Problem Description 给定k个字符串 ...
- vue 弹出框挂载富文本,富文本()无法实例化问题
因为elementUI的dialog组件,他是v-if渲染,再页面刚加载时,这个弹出框还未进行挂载,我们就让他v-show显示. ,富文本实例再mounted里面挂载即可
- Arthas 使用的各类方式
简介: Arthas 是阿里巴巴开源的 Java 诊断工具.让我们能够在线排查项目发生的问题.除了知道它的存在之外,我们也需要知道我们如何去安装使用它,以便于提高我们日常开发解决 BUG 的效率. A ...
- 从技术到科学,中国AI向何处去?
简介: 如果从达特茅斯会议起算,AI已经走过65年历程,尤其是近些年深度学习兴起后,AI迎来了空前未有的繁荣.不过,最近两年中国AI热潮似乎有所回落,在理论突破和落地应用上都遇到了挑战,外界不乏批评 ...
