Atcoder Regular Contest 167

卡 B 下大分了。

A. Toasts for Breakfast Party

发现题意是让方差尽可能小，就是让 \(A\) 里的值尽可能接近。

所以从小到大排个序，把 \(A_{N,\dots,N-M+1}\) 依次放进 \(1,2,\dots,M\)，再把 \(A_{N-M,\dots,1}\) 依次放进 \(M,M-1,\dots,2M-N+1\) 就赢了。

---

B. Product of Divisors

大家快看，这里有一个试图在质因数分解后的指数上推点式子，于是卡 B 1h 的樱雪喵 /cf

Description

给定 \(A,B\)，问 \(A^B\) 所有因数的积不断除以 \(A\)，最多能除几次。

\(A\le 10^{12},B\le 10^{18}\)。

Solution

发现因数是成对的，对每个因数都有 \(x\times \frac{A^B}{x}=A^B\)，设 \(A^B\) 的因数个数为 \(n\)。

如果 \(n\) 是偶数，把因数两两分成 \(\frac{n}{2}\) 对，每对的积都是 \(A^B\)，\(A^B\) 的因数之积就是 \(A^{(Bn/2)}\)，答案是 \(\frac{Bn}{2}\)。

如果是奇数，说明 \(A^B\) 是完全平方数，我们把这个数单独拆出来考虑，\(A^B\) 的因数之积是 \(A^{B(n-1)/2}\times \sqrt{A^B}\)，答案也是这个。

注意完全平方数分为 \(A\) 本身是完全平方数和 \(B\) 是偶数两种情况。

于是就做完了，时间复杂度瓶颈在质因数分解，\(O(\sqrt{A})\)。

Code

bool flag=0;
signed main()
{
    A=read(),B=read();
    if((int)sqrt((long long)A)*(int)sqrt((long long)A)==A) flag=1;
    for(int i=2;i*i<=A;i++)
    {
        if(A%i==0)
        {
            a[++cnt]=i;
            while(A%i==0) b[cnt]++,A/=i;
        }
    }
    if(A>1) b[++cnt]=1;
    int res=1;
    for(int i=1;i<=cnt;i++) res=res*(b[i]*B%mod+1)%mod;
    if(B%2==0||flag) res=(res+mod-1)%mod;
    res=res*qpow(2,mod-2)%mod*B%mod;
    if(B%2==0||flag) res=(res+B/2)%mod;
    cout<<(long long)res<<endl;
    return 0;
}

---

C. MST on Line++

完全不会做，人菜，没救了。

Description

给定正整数 \(n,K\) 和一个长度为 \(n\) 的序列 \(A\)。对于一个 \(1\sim n\) 的排列 \(P\)，我们定义 \(f(P)\) 为以下问题的答案：

给一个 \(n\) 个点的无向带权图，对于两点 \(i<j\)，当且仅当 \(j-i\le K\) 时，它们之间有边，边权为 \(\max(A_{P_i},A_{P_j})\)。

求这个图的最小生成树边权和。

对于所有可能的排列 \(P\)，求出它们的 \(f(P)\) 之和，答案对 \(998\,244\,353\) 取模。

\(1\le K< N\le 5000\)，\(1\le A_i \le 10^9\)。

Solution

发现我们只要求出每条边被选了几次，就可以统计出它们的权值和。

考虑 Kruskal 求最小生成树的过程，发现按边权排序后，我们会选择哪些边只与边之间的大小关系有关，与具体的边权无关。那么我们把 \(A_i\) 升序排序后，令第 \(i\) 类边表示边权为 \(A_i\) 的边，就可以只关心每类边分别选了几次。

考虑如下的子问题：

给定一个边权的限制 \(a\) 和一个排列 \(P\)，对于 \(i<j\)，\(i,j\) 之间有无权边当且仅当 \(j-i\le K\) 且 \(\max(P_i,P_j)\le a\)。求在边之间不形成环的条件下最多选择几条边。

对于一个排列 \(P\)，边权为 \(A_i\) 的边被选择的条数就是 \(a=i\) 时的答案减掉 \(a=i-1\) 时的答案。

设 \(f_{i}\) 表示所有排列 \(P\) 在 \(a=i\) 时该子问题的答案之和。那么有：

\[ans=\sum_{i=2}^{n} A_i(f_i-f_{i-1})
\]

考虑 \(f_i\) 怎么求。

对于一个排列 \(P\)，我们令所有 \(P_j\le i\) 的下标 \(j\) 构成集合 \(Q\)，\(Q\) 中的元素升序排序。因为边权是取 \(\max\)，不在 \(Q\) 内的点一定没有任何连边。

故所有 \(Q_j-Q_{j-1}\le K\) 的下标之间都有连边，且把它们都选上一定是不劣的。对于一个排列 \(P\) 的答案就是 \(\sum\limits_{j=2}^i [Q_j-Q_{j-1}\le K]\)。

枚举一个 \(j\)，对于所有排列计算满足 \(Q_j-Q_{j-1}\le K\) 的数量。\(Q_j-Q_{j-1}=k\) 的排列有 \(\binom{n-k}{i-1}\) 个，\(\le K\) 的就有 \(\sum\limits_{j=1}^K \binom{n-j}{i-l}\) 个。那么一共有 \(i-1\) 对相邻的下标，一个 \(Q\) 序列对答案的贡献是 \((i-1)\sum\limits_{j=1}^K\binom{n-j}{i-l}\)。

一个 \(Q\) 序列对应的排列 \(P\) 的个数是 \(i!(n-i)!\)，最终的式子是

\[f_i=i!(n-i)!(i-1)\sum_{j=1}^K \binom{n-j}{i-1}
\]

求 \(f_i\) 的时间复杂度为 \(O(nK)\)，求答案的时间复杂度为 \(O(n)\)。

Code

#define int long long
const int N=5005,mod=998244353;
int n,K,a[N];
int f[N],jc[N],c[N][N];
il void init(int mx)
{
    for(int i=0;i<=mx;i++)
        for(int j=0;j<=i;j++) c[i][j]=j?(c[i-1][j-1]+c[i-1][j])%mod:1;
}
signed main()
{
    n=read(),K=read(); init(n);
    for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+n+1);
    jc[0]=1;
    for(int i=1;i<=n;i++) jc[i]=jc[i-1]*i%mod;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=K;j++) f[i]=(f[i]+jc[i]*jc[n-i]%mod*(i-1)%mod*c[n-j][i-1]%mod)%mod;
    // for(int i=1;i<=n;i++) cout<<"f "<<i<<" "<<f[i]<<endl;
    int ans=0;
    for(int i=1;i<=n;i++) ans=(ans+a[i]*(f[i]+mod-f[i-1])%mod)%mod;
    printf("%lld\n",ans);
    return 0;
}

---

D. Good Permutation

Description

对于一个 \((1,2,\dots,N)\) 的排列 \(Q\)，称其是好的，当且仅当

• 对于每个整数 \(i \in [1,N]\)，在若干次 \(i \gets Q_i\) 后能够得到 \(i=1\)。

给定一个排列 \(P\)，每次操作可以交换两个数。使用最小的操作次数，使得 \(P\) 成为一个好的排列，若有多种解，输出字典序最小的。

Solution

怎么连着两场 D<C 呢？

对于每个 \(i\)，我们连边 \(i\to P_i\)，那么这张图形成了若干个不相交的环。\(P\) 是一个好的排列当且仅当图上只有一个环。

从小到大依次贪心确定每一位的值，设当前位为 \(i\)：

• 如果存在至少一个 \(P_j=u,j>i\)，满足 \(i,j\) 不在一个环且 \(u<P_i\)，我们找到最小的 \(u\)，并 \(\text{swap}(P_i,P_j)\)。
• 否则我们不希望字典序变大，尽量不换。但如果 \(i\) 是它所在连通块的最后一个位置，必须要换，找到后面最小的 \(u\)，设 \(P_j=u\)，并 \(\text{swap}(P_i,P_j)\)。

判断是否在一个环使用并查集，用一个 set 维护每个连通块之间的大小关系。

Code

const int N=2e5+5;
#define pii pair<int,int>
#define fi first
#define se second
int n,a[N];
int fa[N],mn[N],siz[N],pos[N];
set<pii> s;
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
void merge(int x,int y)
{
    x=find(x),y=find(y); if(x==y) return;
    s.erase(pii(mn[x],x)),s.erase(pii(mn[y],y));
    fa[x]=y,siz[y]+=siz[x],mn[y]=min(mn[y],mn[x]);
    s.insert(pii(mn[y],y));
}
int main()
{
    int T=read();
    while(T--)
    {
        s.clear();
        n=read();
        for(int i=1;i<=n;i++) a[i]=read(),pos[a[i]]=i;
        for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1,mn[i]=i,s.insert(pii(i,i));
        for(int i=1;i<=n;i++) merge(i,a[i]);
        for(int i=1;i<=n;i++)
        {
            if(s.size()==1) break;
            auto it=s.begin();
            while(find(it->se)==find(i)) it++;
            int u=it->fi;
            if(u<a[i]||siz[find(i)]==1)
            {
                int j=pos[u]; swap(a[i],a[j]),swap(pos[a[i]],pos[a[j]]);
                merge(i,j);
            }
            siz[find(i)]--;
        }
        for(int i=1;i<=n;i++) printf("%d ",a[i]);
        printf("\n");
    }
    return 0;
}

E. One Square in a Triangle

Description

多组询问，每次给定一个数 \(S\)，要求构造一个符合如下条件的三角形：

• 三角形的顶点都在格点上；
• 面积为 \(\frac{S}{2}\)；
• 恰好包含了一个顶点在格点上的 \(1\times 1\) 的正方形（换句话说，恰好包含一个完整的格子）

\(T\le 10^5,S\le 10^8\)。

Solution

做法参考部分题解，画了几个图。

设三角形的三个顶点分别为 \(a,b,c\)。整体平移这个三角形不影响答案，所以钦定 \(a=(0,0)\) 以简化计算。

首先 \(S\) 为偶数的情况，我们可以钦定三角形的底为 \(2\)，令 \(a=(0,0),b=(2,0),c=(\frac{S}{2},\frac{S}{2})\)。

这在 \(S\ge 4\) 的情况下可以看出是对的，而手玩可以发现 \(S=2\) 无解。

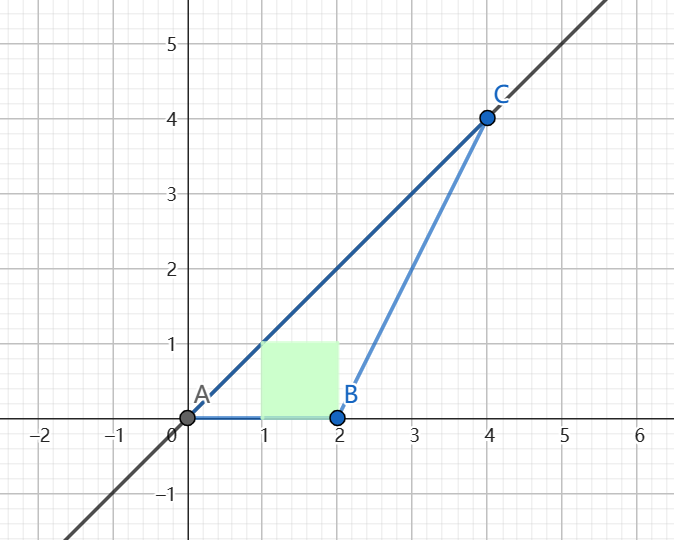
考虑 \(S\) 为奇数的情况。类比偶数时答案的形态：我们确定一条底边，并让剩下的一个点在某条直线上移动。

设 \(b=(x_b,y_b),c=(x_c,y_c)\)，根据三角形的面积公式（可以根据叉积的几何意义证），有

\[S=|x_b y_c - x_c y_b|
\]

\(S\) 是奇数，则 \(x_b y_c\) 与 \(x_c y_b\) 有一个是奇数，即要么 \(x_b,y_c\) 都是奇数，要么 \(x_c,y_b\) 都是奇数。令 \(b=(3,1)\)。

那么式子变成了 \(S=|3y_c - x_c|\)。

要令 \(3y_c\) 和 \(x_c\) 的奇偶性始终不同，考虑钦定 \(y_c=x_c+1\)。答案即为 \(a=(0,0),b=(3,1),c=(\frac{S-3}{2},\frac{S-1}{2})\)。



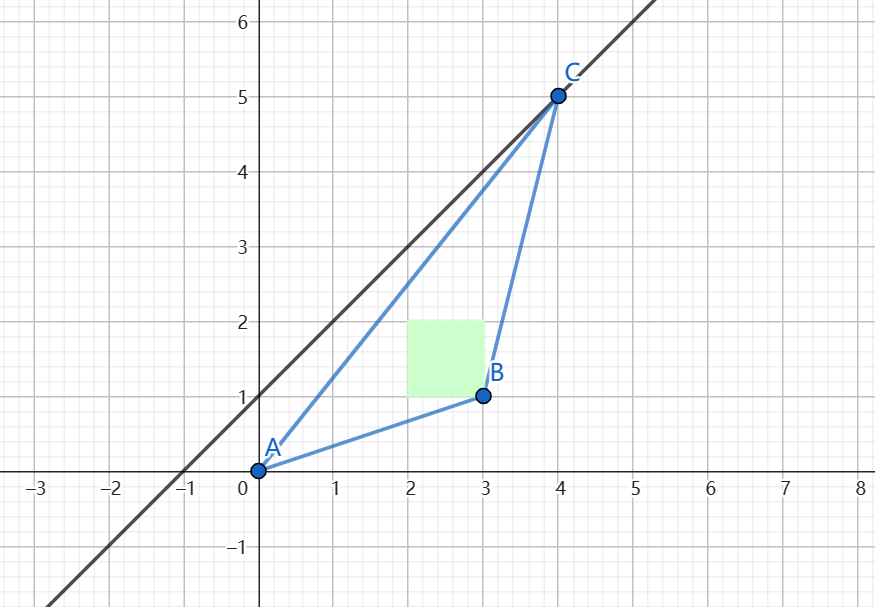
如图，在 $S\ge 9 $ 时满足条件。

手玩小于 \(9\) 的情况，发现 \(S=1,3,5,7\) 均无解。

int T,S;
int main()
{
    T=read();
    while(T--)
    {
        S=read();
        if(S<9&&(S&1)||S==2) {printf("No\n");continue;}
        printf("Yes\n");
        if(S&1) printf("0 0 3 1 %d %d\n",(S-3)/2,(S-1)/2);
        else printf("0 0 2 0 %d %d\n",S/2,S/2);
    }
    return 0;
}

---

F. Tree Tree Tree

不会。