2021-03-21：给定一棵二叉树的头节点head，求以head为头的树中，最小深度是多少？

2021-03-21：给定一棵二叉树的头节点head，求以head为头的树中，最小深度是多少？

福大大 答案2021-03-21：

1.递归。

2.莫里斯遍历。

代码用golang编写，代码如下：

package main

import "fmt"

func main() {
    head := &TreeNode{}
    head.Left = &TreeNode{}
    head.Right = &TreeNode{}
    head.Right.Right = &TreeNode{}

    ret := minHeight1(head)
    fmt.Println("1.递归:", ret)

    ret = minHeight2(head)
    fmt.Println("2.莫里斯遍历：", ret)
}

//Definition for a binary tree node.
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

const INT_MAX = int(^uint(0) >> 1)

func minHeight1(head *TreeNode) int {
    if head == nil {
        return 0
    }
    leftVal := minHeight1(head.Left)
    rightVal := minHeight1(head.Right)
    return 1 + getMin(leftVal, rightVal)
}

// 根据morris遍历改写
func minHeight2(head *TreeNode) int {
    if head == nil {
        return 0
    }
    cur := head
    var mostRight *TreeNode
    curLevel := 0
    minHeight := INT_MAX
    for cur != nil {
        mostRight = cur.Left
        if mostRight != nil {
            rightBoardSize := 1
            for mostRight.Right != nil && mostRight.Right != cur {
                rightBoardSize++
                mostRight = mostRight.Right
            }
            if mostRight.Right == nil { // 第一次到达
                curLevel++
                mostRight.Right = cur
                cur = cur.Left
                continue
            } else { // 第二次到达
                if mostRight.Left == nil {
                    minHeight = getMin(minHeight, curLevel)
                }
                curLevel -= rightBoardSize
                mostRight.Right = nil
            }
        } else { // 只有一次到达
            curLevel++
        }
        cur = cur.Right
    }
    finalRight := 1
    cur = head
    for cur.Right != nil {
        finalRight++
        cur = cur.Right
    }
    if cur.Left == nil && cur.Right == nil {
        minHeight = getMin(minHeight, finalRight)
    }
    return minHeight
}
func getMin(a int, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

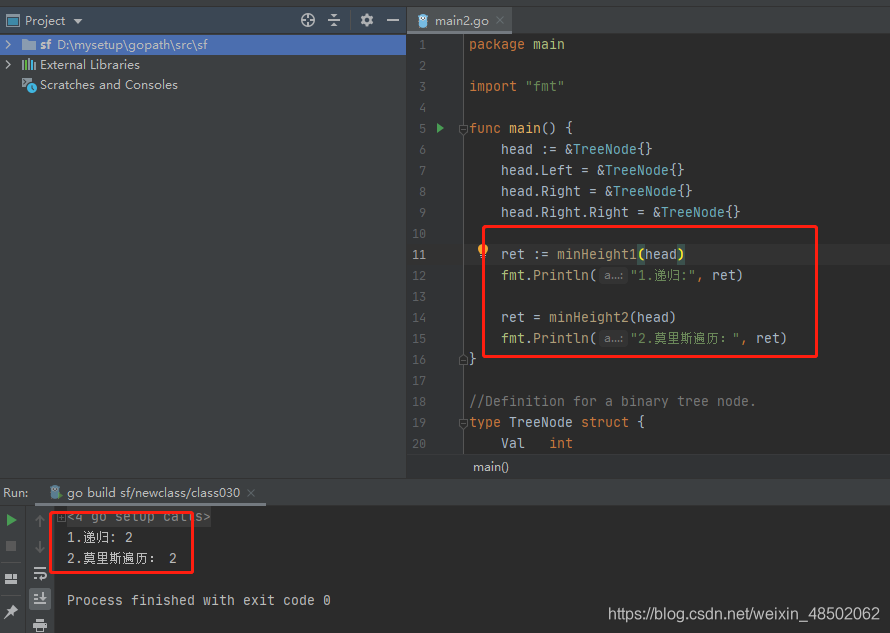
执行结果如下：

---

左神java代码

评论