2021-11-15：四数相加 II。给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：0 ＜= i,

2021-11-15：四数相加 II。给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：0 <= i, j, k, l < n；nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0。力扣454。

答案2021-11-15：

nums1+nums2存map。然后求nums3 +nums4 ，在map里找到相反数，就添加到结果里。
时间复杂度：O(N2)。
额外空间复杂度：O(N2)。

代码用golang编写。代码如下：

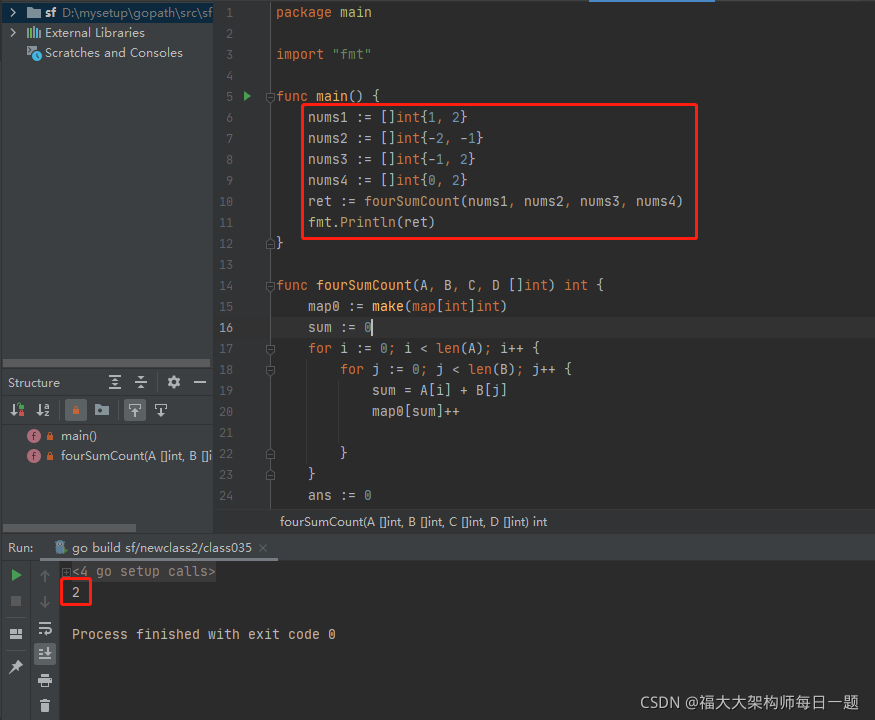
package main

import "fmt"

func main() {
    nums1 := []int{1, 2}
    nums2 := []int{-2, -1}
    nums3 := []int{-1, 2}
    nums4 := []int{0, 2}
    ret := fourSumCount(nums1, nums2, nums3, nums4)
    fmt.Println(ret)

}

func fourSumCount(A, B, C, D []int) int {
    map0 := make(map[int]int)
    sum := 0
    for i := 0; i < len(A); i++ {
        for j := 0; j < len(B); j++ {
            sum = A[i] + B[j]
            map0[sum]++

        }
    }
    ans := 0
    for i := 0; i < len(C); i++ {
        for j := 0; j < len(D); j++ {
            sum = C[i] + D[j]
            if _, ok := map0[-sum]; ok {
                ans += map0[-sum]
            }
        }
    }
    return ans
}

执行结果如下：

---

左神java代码