实例：（[Flappy Bird Q-learning]

目录

• 实例：（Flappy Bird Q-learning）
  • 问题分析
  • 关于Q
  • 训练
  • 成果

实例：（Flappy Bird Q-learning）

问题分析

让小鸟学习怎么飞是一个强化学习（reinforcement learning）的过程，强化学习中有状态(state)、动作(action)、奖赏(reward)这三个要素。智能体（Agent，在这里就是指我们聪明的小鸟）需要根据当前状态来采取动作，获得相应的奖赏之后，再去改进这些动作，使得下次再到相同状态时，智能体能做出更优的动作。

状态的选择 在这个问题中，状态的提取方式可以有很多种：比如说取整个游戏画面做图像处理啊，或是根据小鸟的高度和管子的距离啊。在这里选用的是跟SarvagyaVaish项目相同的状态提取方式，即取小鸟到下一根下侧管子的水平距离和垂直距离差作为小鸟的状态：

（图片来自Flappy Bird RL by SarvagyaVaish）

记这个状态为，为水平距离，为垂直距离。

动作的选择 小鸟只有两种动作可选：1.向上飞一下，2.什么都不做。

奖赏的选择 这里采用的方式是：小鸟活着时，每一帧给予1的奖赏；若死亡，则给予-1000的奖赏；若成功经过一个水管，则给予50的奖赏。

关于Q

提到Q-learning，我们需要先了解Q的含义。

Q为动作效用函数（action-utility function），用于评价在特定状态下采取某个动作的优劣，可以将之理解为智能体（Agent，我们聪明的小鸟）的大脑。我们可以把Q当做是一张表。表中的每一行是一个状态，每一列（这个问题中共有两列）表示一个动作（飞与不飞）。

例如：

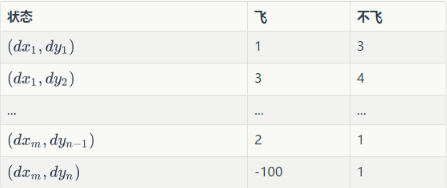
这张表一共 行，表示 个状态，每个状态所对应的动作都有一个效用值。训练之后的小鸟在某个位置处飞与不飞的决策就是通过这张表确定的。小鸟会先去根据当前所在位置查找到对应的行，然后再比较两列的值（飞与不飞）的大小，选择值较大的动作作为当前帧的动作。

训练

那么这个Q是怎么训练得来的呢，贴一段伪代码。

Initialize Q arbitrarily //随机初始化Q值
Repeat (for each episode): //每一次游戏，从小鸟出生到死亡是一个episode
    Initialize S //小鸟刚开始飞，S为初始位置的状态
    Repeat (for each step of episode):
        根据当前Q和位置S，使用一种策略，得到动作A //这个策略可以是ε-greedy等
        做了动作A，小鸟到达新的位置S'，并获得奖励R //奖励可以是1，50或者-1000
        Q(S,A) ← (1-α)*Q(S,A) + α*[R + γ*maxQ(S',a)] //在Q中更新S
        S ← S'
    until S is terminal //即到小鸟死亡为止

其中有两个值得注意的地方

1.“根据当前Q和位置S，使用一种策略，得到动作A，这个策略可以是ε-greedy等。”

这里便是题主所疑惑的问题，如何在探索与经验之间平衡？假如我们的小鸟在训练过程中，每次都采取当前状态效用值最大的动作，那会不会有更好的选择一直没有被探索到？小鸟一直会被桎梏在以往的经验之中。而假若小鸟在这里每次随机选取一个动作，会不会因为探索了太多无用的状态而导致收敛缓慢？

于是就有人提出了ε-greedy方法，即每个状态有ε的概率进行探索（即随机选取飞或不飞），而剩下的1-ε的概率则进行开发（选取当前状态下效用值较大的那个动作）。ε一般取值较小，0.01即可。当然除了ε-greedy方法还有一些效果更好的方法，不过可能复杂很多。

以此也可以看出，Q-learning并非每次迭代都沿当前Q值最高的路径前进。

\2.

这个就是Q-learning的训练公式了。其中α为学习速率（learning rate），γ为折扣因子（discount factor）。根据公式可以看出，学习速率α越大，保留之前训练的效果就越少。折扣因子γ越大，所起到的作用就越大。但指什么呢？

小鸟在对状态进行更新时，会考虑到眼前利益（R），和记忆中的利益（）。

指的便是记忆中的利益。它是指小鸟记忆里下一个状态的动作中效用值的最大值。如果小鸟之前在下一个状态的某个动作上吃过甜头（选择了某个动作之后获得了50的奖赏），那么它就更希望提早地得知这个消息，以便下回在状态可以通过选择正确的动作继续进入这个吃甜头的状态。

可以看出，γ越大，小鸟就会越重视以往经验，越小，小鸟只重视眼前利益（R）。

根据上面的伪代码，就可以写出Q-learning的代码了。

成果

训练后的小鸟一直挂在那里可以飞到几千分~