力扣303(java)-区域和检索-数组不可变(简单)
题目:
给定一个整数数组 nums,处理以下类型的多个查询:
计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + ... + nums[right] )
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
提示:
1 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/range-sum-query-immutable
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路:
利用前缀和,将前缀和数组sum的长度设置为n+1,并将sum的第0个元素设置为0。将数组的数和前缀和列出,找出通式。

代码:
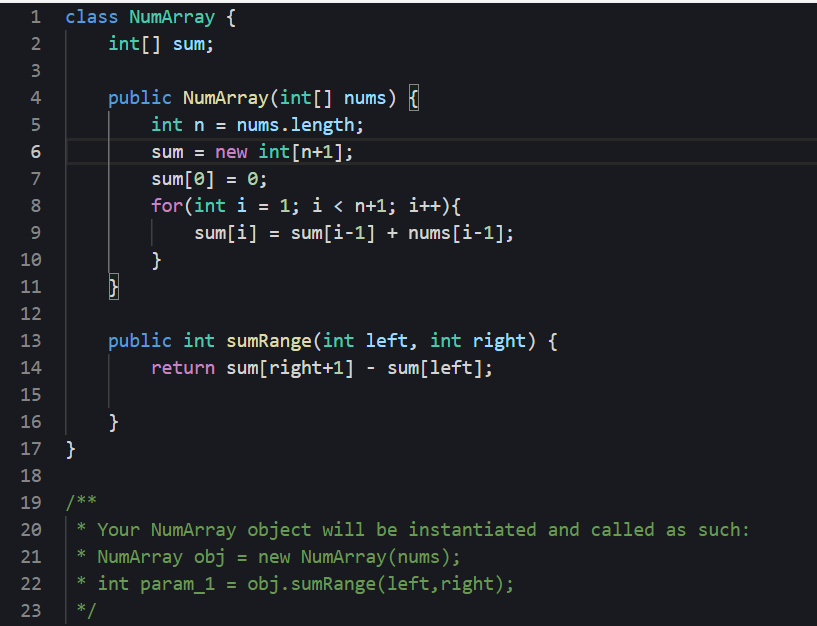
力扣303(java)-区域和检索-数组不可变(简单)的更多相关文章
- Java实现 LeetCode 303 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变 给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点. 示例: 给定 nums = [-2, 0, 3, ...
- [Swift]LeetCode303. 区域和检索 - 数组不可变 | Range Sum Query - Immutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive ...
- 【leetcode 简单】 第七十九题 区域和检索 - 数组不可变
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点. 示例: 给定 nums = [-2, 0, 3, -5, 2, -1],求和函数 ...
- Java实现 LeetCode 307 区域和检索 - 数组可修改
307. 区域和检索 - 数组可修改 给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点. update(i, val) 函数可以通过将下标 ...
- Java实现 LeetCode 304 二维区域和检索 - 矩阵不可变
304. 二维区域和检索 - 矩阵不可变 给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2). Range Sum Qu ...
- Leetcode 304.二维区域和检索-矩阵不可变
二维区域和检索 - 矩阵不可变 给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2). 上图子矩阵左上角 (row1, c ...
- 力扣Leetcode 面试题56 - I. 数组中数字出现的次数
面试题56 - I. 数组中数字出现的次数 一个整型数组 nums 里除两个数字之外,其他数字都出现了两次.请写程序找出这两个只出现一次的数字.要求时间复杂度是O(n),空间复杂度是O(1). 示例 ...
- 【力扣】922. 按奇偶排序数组 II
给定一个非负整数数组 A, A 中一半整数是奇数,一半整数是偶数. 对数组进行排序,以便当 A[i] 为奇数时,i 也是奇数:当 A[i] 为偶数时, i 也是偶数. 你可以返回任何满足上述条件的数组 ...
- LeetCode--303--区域和检索 - 数组不可变
问题描述: 给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点. 示例: 给定 nums = [-2, 0, 3, -5, 2, -1 ...
- LeetCode 304. Range Sum Query 2D - Immutable 二维区域和检索 - 矩阵不可变(C++/Java)
题目: Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper ...
随机推荐
- Educational Codeforces Round 141:B. Matrix of Differences
一.来源:Problem - B - Codeforces 二.题面 三.思路 我们先从一维思考如何构造尽可能多的数值差.以n=2为例,此时有1,2,3,4数,其中构成差值为3的方案有一个1,4,构成 ...
- 一次对requirements环境的配置
事情是这样的,我需要跑通一个代码,因此要配置环境,但是并不能利用requirements中给的指令直接配置,于是开始找一些其他的解决方法.作为一名小白,总是绕很多弯路. 记下一些蜿蜒. 首先,摘录re ...
- Android Studio导出APP的数据库db文件
原文地址:Android Studio导出APP的数据库db文件 | Stars-One的杂货小窝 最近项目开发需要使用到Android内置的Sqlite存数据,但是公司里没有对应的调试环境,只能让现 ...
- js实现回调功能实例
所谓js回调,本人认为无非就是一个函数的参数是另外一个函数,而作为参数的函数就称之为回调函数 <script type="text/javascript"> //要请 ...
- 数据结构-Hash常见操作实践
数据结构-Hash常见操作实践 目录介绍 01.什么是哈希算法 02.哈希算法的应用 03.安全加密的场景 04.唯一标识的场景 05.数据校验的场景 06.散列函数的场景 07.Git版本的控制 0 ...
- 记录--整会promise这8个高级用法
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 发现很多人还只会promise常规用法 在js项目中,promise的使用应该是必不可少的,但我发现在同事和面试者中,很多中级或以上的前端 ...
- 神经网络——基于sklearn的参数介绍及应用
一.MLPClassifier&MLPRegressor参数和方法 参数说明(分类和回归参数一致): hidden_layer_sizes :例如hidden_layer_sizes=(50, ...
- C# 二维码生成、识别
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- 初学 FSMC - 外扩SRAM(三)
1. FSMC相关函数 //FSMC初始化 void FSMC_NORSRAMInit(FSMC_NORSRAMInitTypeDef* FSMC_NORSRAMInitStruct); //FSMC ...
- python整理1992、2009国家标准学科分类及代码数据并存入MySQL数据库
文件内容 处理结果 代码 1 import pandas as pd 2 import pymysql 3 4 5 def get_subject_1992(): 6 res={} 7 the_for ...
