『数据结构』RMQ问题

RMQ（Range Minimum/Maximum Query），即区间最值问题。

对于长度为 n 的数列 A ，回答若干查询 RMQ(A,i,j)(i,j<=n) ，返回数列 A 中下标在 i,j 里的最大（小）值。

相关算法

1. 朴素（搜索），时间复杂度：\(O(n)-O(q \times n)\) ，在线；
2. 线段树，时间复杂度：$O(n)-O(q\times logn) $，在线；
3. ST（动态规划），时间复杂度：\(O(n\times logn)-O(q)\)，在线；
4. RMQ标准算法，先规约为LCA，再规约成约束RMQ ，时间复杂度：\(O(n)-O(q)\)，在线。

ST 算法

假设当前题目要求区间最小值，我们令 dp[i][j] 代表从 i 开始，长度为\(2^{j}\)这段区间的最小值。

于是便有：\(dp[i][j]=min(dp[i][j-1],dp[i+^{j-1}][j-1])\)

分析可知，\(dp[i][j-1]\)代表从 i 开始，长度为\(2^{j}\)区间一半中的最小值，而 \(dp[i+2^{j-1}][j-1]\)即为区间的另一半。

即为区间的另一半。

最终（从下往上看）：

	\(dp[0][*]\)	\(dp[1][*]\)	\(dp[2][*]\)	\(dp[3][*]\)	\(dp[4][*]\)	\(dp[5][*]\)	\(dp[6][*]\)	\(dp[7][*]\)
\(dp[*\)][3]	\(1\)
\(dp[*\)][2]	\(1\)	\(1\)	\(1\)	\(5\)	\(2\)
\(dp[*][1]\)	\(3\)	\(1\)	\(1\)	\(5\)	\(7\)	\(6\)	\(2\)
\(dp[*][0]\)	\(4\)	\(3\)	\(1\)	\(5\)	\(7\)	\(8\)	\(6\)	\(2\)

预处理

根据状态转移方程，首先指定当区间长度为\(2^{0}\)时的各初始值，随后推出后面的结果。

void ST_Init(const vector<int> &A) {
    int n=A.size();
    for (int i=0; i<n; i++)
        dp[i][0]=A[i];
    for (int j=1; (1<<j)<=n; j++)
        for (int i=0; i+(1<<j)<=n; i++)
            dp[i][j]=min(dp[i][j-1], dp[i+(1<<(j-1))][j-1]);
}

查询

预处理出整个 dp 数组以后，查询操作很简单，令 k 为满足\(2^{k} \leq R-L+1\)的最大整数，则以 L 开头、以 R 结尾的两个长度为\(2^{k}\)的区间合起来即覆盖了查询区间 [L,R] 。

int RMQ(int L, int R) {
    int k=0;
    while ((1<<(k+1))<=R-L+1) k++;
    return min(dp[L][k], dp[R-(1<<k)+1][k]);
}

嗯！怎么说呢？感觉线段树在这种类型的题目中好像是最万能的方法了。

无论是 [点修改+查询] 还是 [区间修改+查询] ，它都可以做到 \(O(logn)\)的复杂度，而且在线段树中我们也可以维护好多东西（区间和、最值等等）。

对于一维中的线段树，我们想要查询某个区间的最值，首先就应该建树咯~（具体方法省略）

而在查询时，我们可以从根节点向下递归搜索，如下图，假设查询区间为 [2,6] 。

将 [2,6] 这一个大区间分解为不相交的三个小区间 [2,3]、[4,5]、[6] ，而最终的结果便由这三个节点中所维护的信息决定的！

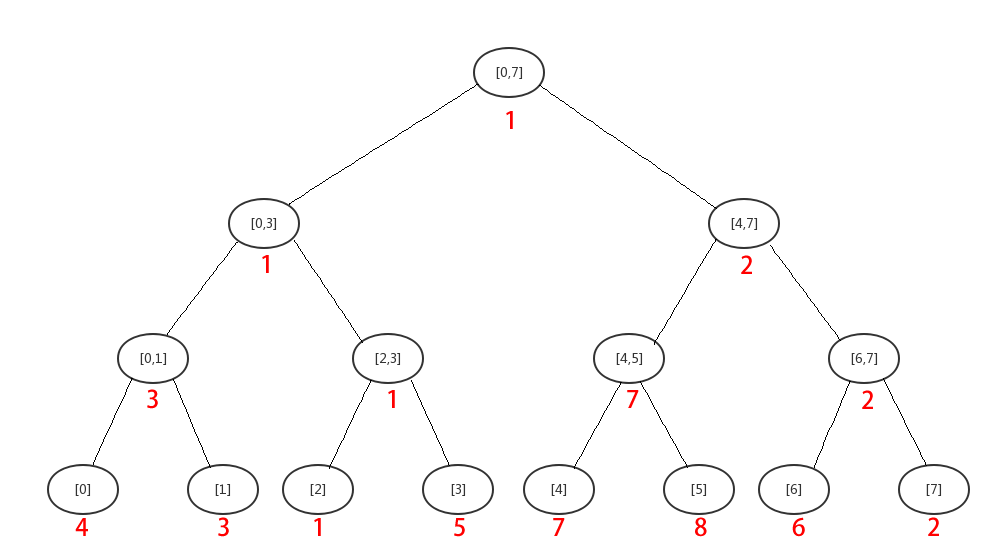
我们假设查询还是区间最小值，于是最终的结果为\(\min(1,7,6)=1\)

线段树可以解决普通的 [点/区间] 修改+查询 ，当然它也可以解决 树中的路径权值 修改+查询（树链剖分）。