[考试反思]1101csp-s模拟测试97：人品

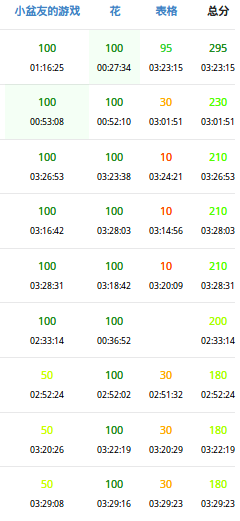
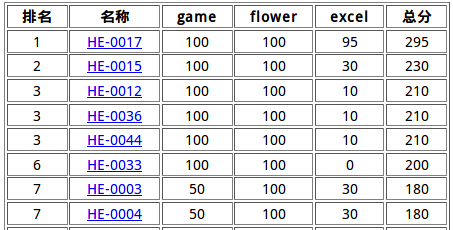
上来粘6个图皮一下。（以后粘排行榜是不是都应该粘两份啊。。。文件出入的确挺难受的）

话说最近RP为什么会这么高啊？？？我干什么好事了？？？不知道。

这次考试的题挺有水准的，但是我的分数挺没水准的。

T1打表找规律。严格来说不是打表找规律，是看样例找规律然后手模一个表“验证”了规律。

先做的T2简单dp这个没的说，数据范围出到$10^{100}$复杂度也能接受（但是要写高精了），出题人可能把T2弄成送分题了。

可是都不用矩阵快速幂，所以就这么水过了。

T3的话出题人想复杂了。（？）

拿二维线段树能做复杂度也没毛病，那么为什么要分那么多类讨论呢？

所以说我还是没什么水准。骗分能力倒是不错。（虽说这个骗分好像挺有脸的。。）

而且T3好像过不去对拍，在n超过1000的时候大概每2400组数据错一个（在值域很小的时候），可能是暴力挂了？

当然对拍让我发现了一处错误从WA5里拯救了我。

也不知道这样的RP能维持到什么时候吧。。。

记得数组开大！！！不爆内存上限还不会算的时候为什么不开大一点呢？

丢了个AK。但不是很难过。这要是平时可能又要跳起来了吧2333

T1：小盆友的游戏

要听一下找规律的过程吗？证明的话还是找$LNC$或者是看题解吧。

题解里都说了这是打表找规律题那么为什么不打表呢？

首先看样例，6个？出题人这么好？

其实就提醒了我这需要找规律。

然后根据部分分和前4个样例直接拿下50分。

然后看第5个，相较于第二个，它多了一个跟班，答案少了1。

然后看第6个，相较于第三个，它多了两个跟班，答案少了3。

根据1->1和2->3，那么猜测一下数列，要么是1/3/5/7要么是1/3/7/15。

直觉让我们选择后者，因为后者就是前50分部分分的式子！（有小变化，指数少了1）

但是这样很不严谨。所以首先我们把前4个样例代入后来发现的式子，发现满足规律。

然后把n=4的4种情况全部都画出来手解方程，发现4种状态都满足。

（如果你还不放心，可以像cbx一样把n=5的6中情况也来一遍，但是花费的时间可能比较长）

其实我也不是这么不正经，我尝试dp来着，但是没做出来，发现没有搜索的部分分，于是就认为这是一个结论题。

期望得分：50分。

 #include<cstdio>
 #define mod 1000000007
 int cnt[],n,ans,pw[];
 int main(){
     freopen("game.in","r",stdin);
     freopen("game.out","w",stdout);
     scanf("%d",&n);
     for(int i=,x;i<=n;++i)scanf("%d",&x),cnt[x>?x:]++;
     for(int i=;i<=n;++i)pw[i]=((pw[i-]<<)+)%mod;
     ans=pw[n-];
     for(int i=;i<=n;++i)ans=(ans-pw[cnt[i]]+mod)%mod;
     printf("%d\n",ans);
 }

T2：花

没有矩阵快速幂的矩阵快速幂优化dp题。

状态只有：1连击，2连击，3连击，之前3连击过而现在只有1连击，之前3连击过而现在有2连击。以及已经非法的状态。

 #include<cstdio>
 #define mod 1000000007
 long long dp[][],S,N;
 int main(){
     freopen("flower.in","r",stdin);
     freopen("flower.out","w",stdout);
     int t;scanf("%d",&t);
     while(t--){
         scanf("%lld%lld",&N,&S);S--;
         dp[][]=S+;
         for(int i=;i<=N;++i)
             dp[][i]=(dp[][i-]+dp[][i-])*S%mod,
             dp[][i]=dp[][i-],
             dp[][i]=dp[][i-],
             dp[][i]=(dp[][i-]+dp[][i-]+dp[][i-])*S%mod,
             dp[][i]=dp[][i-];
         printf("%lld\n",(dp[][N]+dp[][N]+dp[][N])%mod);
     }
 }

T3：表格

强烈呼吁这道题提交之前检查文件！一卡3分钟！！！

update太多了于是直接说在前面：我的时空复杂度都是常数较小的$O(n^2)$。（暴力碾标算2333怪不得开了8s）

所以我是考场上水过的。正在看正解。

时空复杂度都是$O(nlog^2n)$的与正解一致。但是空间复杂度常数很大，时间复杂度的常数较小。

update：空间复杂度是错误的！空间复杂度为$O(16n^2)$，所以下文的剪枝很有必要（因为是动态开点所以剪枝可以节约内存）

再update：空间复杂度没那么烂。因为每次查询至多经历$O(log^23n)$个节点所以n次操作的话总的空间最大也就$O(nlog^2n)$

但是其实$O(nlog^23n)$也不满足要求，所以还是需要剪枝。

其实可以在update函数执行时进行空间回收，但是没必要。。。

再再update：QAQ时间复杂度又被hack了。$O(n)$的。。。会被长条卡掉。。。所以总的时空复杂度都是$O(n^2)$

当然如果你打的是动态开点树套树就可以解决这个问题。（好像也被hack了）

所以我最慢的点也才跑0.7s但是我数组没开够

首先说明二维线段树与KD-tree的不同：KD-tree基于读入的序列，而线段树基于值域。

KD-tree在很多情况下都要想两个儿子都要递归，而线段树向两个儿子都要递归的情况最多只会出现$log$次。

考虑一维的线段树，你查询的过程当中经过的节点数一共有$log$个。

而二维的线段树两维互不干扰，这样的话它所经过的节点的控制区间就是两个一维线段树的区间自由组合，最差是$log^2$个。

所以复杂度是正确的。

做法，就是时光倒流（题目中的“Crtl+Z”有一定提示意义）。然后发现你的操作就是：

1。查找当前区间内是否还有空位置，如果有，那么ans+1。

2。把区间内所有位置设置为非空。

区间查询区间修改，不难想到线段树。

为了保证时空复杂度，需要离散化。

update操作就是如果两个儿子中都没有空位，那么你的控制区间就也没有空位了。

这样的话会出现一个问题：离散化之后两个儿子并非紧密相邻的。

所以在离散化的时候需要加入原右端点+1来表示它是紧密相邻的。

然后就没了。代码真的好写线段树才和离散化一般长。

因为空间复杂度很高，所以需要动态开点。（不开行不行我也不知道）

它和KD-tree相似的一点就是要横着切一刀竖着切一刀这么交替的分下去。

为什么不能一直竖着分，分到所需要的节点再一直横着切呢？

因为这样的话不好合并子树信息。其实不需要合并，但是合并之后相当与剪枝。

和四分树还是不太一样的。好像网上有混淆两者概念的。

不管了，就当是我自己yy的吧。我这好像的确不叫二维线段树。

而网上说的二维线段树/四分树的单次操作复杂度最差是$O(n)$的。。。

那么你可以管我打的这个树叫Dee树。嗯。(所以Dee树就是TLE+MLE树啦)

你们可以叫我B哥。

——By Rockstar in 2018.9

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 int xa[],xb[],ya[],yb[],x[],y[],X,Y,n;
 int qxl,qxr,qyl,qyr,lc[],rc[],ans=,res,cnt,rt;char nt[],u[];
 void modify(int &p,int cxl,int cxr,int cyl,int cyr,int opt){
     if(!p)p=++cnt;
     if(nt[p])return;
     if(qxl<=cxl&&cxr<=qxr&&qyl<=cyl&&cyr<=qyr)return nt[p]=,ans+=res,res=,(void);
     if(opt){int mid=cxl+cxr>>;
         if(qxl<=mid)modify(lc[p],cxl,mid,cyl,cyr,);
         if(qxr>mid)modify(rc[p],mid+,cxr,cyl,cyr,);
     }else{int mid=cyl+cyr>>;
         if(qyl<=mid)modify(lc[p],cxl,cxr,cyl,mid,);
         if(qyr>mid)modify(rc[p],cxl,cxr,mid+,cyr,);
     }nt[p]=nt[lc[p]]&nt[rc[p]];
 }
 int main(){
     freopen("excel.in","r",stdin);
     freopen("excel.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i)scanf("%d%d%d%d",&xa[i],&ya[i],&xb[i],&yb[i]),xb[i]--,yb[i]--;
     for(int i=;i<=n;++i)x[i]=xa[i],x[i+n]=xb[i],x[i+n+n]=xb[i]+,y[i]=ya[i],y[i+n]=yb[i],y[i+n+n]=yb[i]+;
     sort(x+,x++n+n+n);sort(y+,y++n+n+n);
     X=unique(x+,x++n+n+n)-x;Y=unique(y+,y++n+n+n)-y;
     for(int i=;i<=n;++i)xa[i]=lower_bound(x+,x+X,xa[i])-x,xb[i]=lower_bound(x+,x+X,xb[i])-x;
     for(int i=;i<=n;++i)ya[i]=lower_bound(y+,y+Y,ya[i])-y,yb[i]=lower_bound(y+,y+Y,yb[i])-y;
     for(int i=n;i;--i)qxl=xa[i],qxr=xb[i],qyl=ya[i],qyr=yb[i],res=,modify(rt,,X,,Y,);
     printf("%d\n",ans);
 }