GNSS学习笔记--坐标转换

GNSS 坐标转换

GNSS计算主要涉及三个坐标系，地心地固坐标系，地理坐标系和站心坐标系。这里主要介绍一下三个坐标的含义和转换公式。

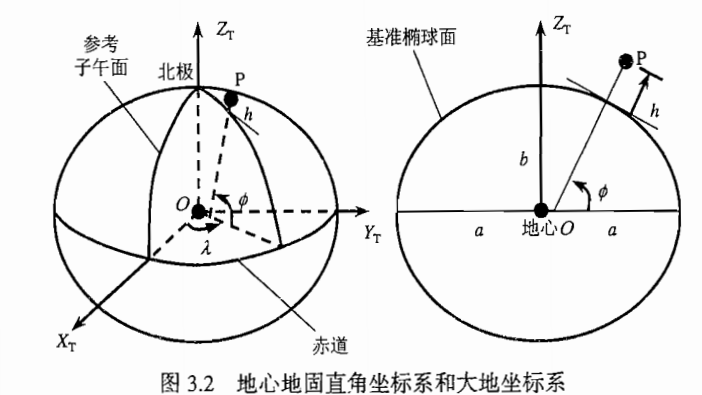
• 地心地固坐标系如图X,Y,Z表示 (ECEF坐标系)，以地心O为坐标原点，Z轴指向协议地球北极，X轴指向参考子午面与地球赤道的交点，也叫地球坐标系。一般GNSS坐标计算都在地心地固坐标系下进行的。由于地球是椭圆形，有WGS-84和CGC2000等多种标准

• 地理坐标系则通过经度(longitude)，纬度(latitude)和高度(altitude)来表示地球的位置，也叫经纬高坐标系(LLA坐标系)。

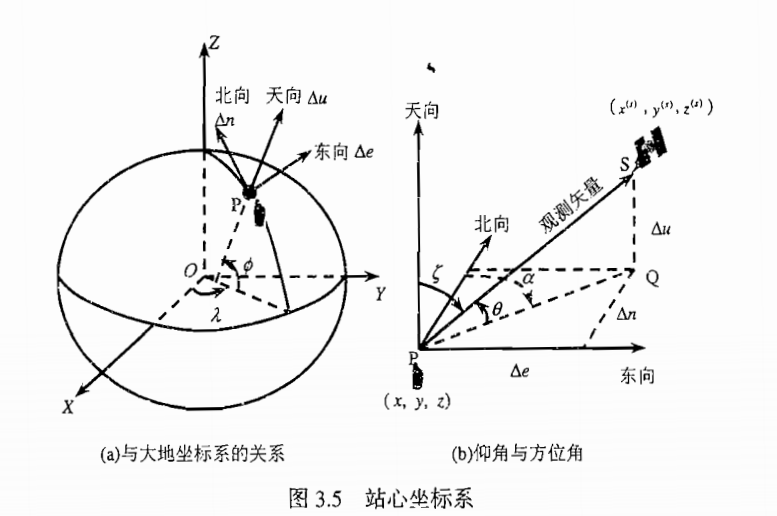
• 站心坐标系以用户所在位置P为坐标原点，三个轴分别指向东向，北向和天向，也叫东北天坐标系(enu坐标系)。站心坐标系的天向方向和地理坐标系的高度方向是一致的。站心坐标系用在惯性导航和卫星俯仰角计算中较多。

参数	WGS-84	CGC200
基准椭球体的长半径a	6378137.0 m	6378137.0 m
基准椭球体的极扁率f	1/298.257223565	1/298.257223563
地球自转角速度We	7.2921151467*1e-5	7.2921151467*1e-5
地球引力和地球质量的乘积GM	3986004.418*1e8	3986004.418*1e8
光速	2.99792458*1e8 m/s	2.99792458*1e8 m/s

LLA坐标系转ECEF坐标系

LLA坐标系下的(lon,lat,alt)转换为ECEF坐标系下点(X,Y,Z)

\[\begin{cases}
X=(N+alt)cos(lat)cos(lon)\\
Y=(N+alt)cos(lat)sin(lon)\\
Z=(N(1-e^2)+alt)sin(lat)
\end{cases}\]

其中e为椭球偏心率，N为基准椭球体的曲率半径
\[\begin{cases}
e^2=\frac{a^2-b^2}{a^2}\\
N=\frac{a}{\sqrt{1-e^2sin^2lat}}
\end{cases}\]

由于WGS-84下极扁率\(f=\frac{a-b}{a}\),偏心率e和极扁率f之间的关系：
\[e^2=f(2-f)\]

坐标转换公式也可以为
\[\begin{cases}
X=(N+alt)cos(lat)cos(lon)\\
Y=(N+alt)cos(lat)sin(lon)\\
Z=(N(1-f)^2+alt)sin(lat)
\end{cases}\]

\[N=\frac{a}{\sqrt{1-f(2-f)sin^2lat}}\]

ECEF坐标系转LLA坐标系

ECEF坐标系下点(X,Y,Z)转换为LLA坐标系下的(lon,lat,alt)

\[lon=arctan(\frac{y}{x})\]
\[alt=\frac{p}{cos(lat)-N}\]
\[lat=arctan\bigg[\frac{z}{p}\bigg(1-e^2\frac{N}{N+alt}\bigg)^{-1}\bigg]\]
\[p=\sqrt{x^2+y^2}\]
一开始lon是未知的，可以假设为0，经过几次迭代之后就能收敛

ECEF坐标系转enu坐标系

用户所在坐标点\(P_0=(x_0,y_0,z_0)\),，计算点\(P=(x,y,z)\)在以点\(P_{0}\)为坐标原点的enu坐标系位置\((e,n,u)\)这里需要用到LLA坐标系的数据，\(P_0\)的LLA坐标点为\(LLA_0=(lon_0,lat_0,alt_0)\)

\[
\begin{gathered}
\left[ \begin{array}{ccc}
\Delta{x}\\\Delta{y}\\\Delta{z}
\end{array}
\right]=
\left[ \begin{array}{ccc}
x\\y\\z\end{array}\right]-
\left[ \begin{array}{ccc}
x_0\\y_0\\z_0\end{array}\right]
\end{gathered}
\]

\[
\begin{gathered}
\left[ \begin{array}{ccc}
e\\n\\u
\end{array}
\right]=S\cdot
\left[ \begin{array}{ccc}
\Delta{x}\\\Delta{y}\\\Delta{z}
\end{array}
\right]
\end{gathered}=
\left[ \begin{array}{ccc}
-sin(lon_0) & cos(lon_0) & 0 \\
-sin(lat_0)cos(lon_0) & -sin(lat_0)sin(lon_0) & cos(lat_0) \\
cos(lat_0)cos(lon_0) & cos(lat_0)sin(lon_0) & sin(lat_0)
\end{array} \right]\cdot
\left[ \begin{array}{ccc}
\Delta{x}\\\Delta{y}\\\Delta{z}
\end{array}
\right]
\]

即坐标变换矩阵\(S=\left[ \begin{array}{ccc} -sin(lon_0) & cos(lon_0) & 0 \\ -sin(lat_0)cos(lon_0) & -sin(lat_0)sin(lon_0) & cos(lat_0) \\ cos(lat_0)cos(lon_0) & cos(lat_0)sin(lon_0) & sin(lat_0) \end{array} \right]\)

enu坐标系转ECEF坐标系

\(S\)为单位正交矩阵
\[\mathbf{S}^{-1}=\mathbf{S}^\mathrm{T}\]
反之
\[
\begin{gathered}
\left[ \begin{array}{ccc}
\Delta{x}\\\Delta{y}\\\Delta{z}\end{array}
\right]=S^{-1}\cdot\left[ \begin{array}{ccc}
e\\n\\u\end{array} \right]=
\mathbf{S}^\mathrm{T}\cdot\left[ \begin{array}{ccc}
e\\n\\u\end{array} \right]
\end{gathered}
\]

LLA坐标系转enu坐标系

上述可以看到，从LLA坐标系转换到enu坐标系有较多计算量，在考虑地球偏心率\(e\)很小的前提下，可以做一定的近似公式计算

\[
\left[ \begin{array}{ccc}
\Delta e\\ \Delta n \\ \Delta u
\end{array}
\right]=
\left[\begin{array}{ccc}
a\cdot cos(lat)\cdot \Delta lon & 0 & 0 \\
0 & a \cdot \Delta lat & 0 \\
0 & 0 & \Delta alt
\end{array}
\right]
\]