用MATLB仿真一个单闭环控制量，同时还存在两个开环控制变量的阶跃响应曲线。（自动控制方法是PID中的P控制。通过查表法直接给开环参数稳态最佳的大小）

实际项目背景：甘肃省，航天510所的LIPS100电推力器。一共有三个控制变量，开环控制变量是：Ia(阳极电流)、mmrf(阳极主流率) 这个阳极主流率是阀门变量，不能够突变，模拟用（大学一年级课，电路分析基础中）类似电感放电的e指数公式。

要求：比例控制参数P可调，阶跃响应在通电前设定幅值3.5~12.8 假设仿真实验时长120S，在第60S时给定阶跃控制信号。

1. 把查表用的TXT文件放到MATLAB当前文件夹路径。fDemandToIa.txt和subBestSchedule_2.txt
2. MATLAB仿真脚本名称为 stepEmulation.m 可以用记事本打开（推荐使用Notepad++）
3. 仿真脚本中用详尽的注释标注了 比例控制参数pParameter以及阶跃控制信号幅值:
4. f_stepaFd = 7  ;    %——————————————————修改阶跃初始值
5. f_stepbFd = 4 ;    %——————————————————修改阶跃终末值

脚本代码如下可供参考，自动化专业毕业的我转行IT做码农：

% M脚本实现的功能是，根据输入的各项参数仿真推力跟随阶跃控制信号的性能
% 作者kangyupeng94@live.cn
% 时间2019年07月18日  甘肃兰州
   clear;close all;
   pParameter = 0.003 ;%——————————————————修改比例控制参数
   f_step0Fd = 0  ;  %启动开机前需求幅值应为0
 % 载入需求推力和阳极电流与主流率之间的查表文件
   fDemandToIa = load('fDemandToIa.txt');
   subBestSchedule_2 = load('subBestSchedule_2.txt');
 % 两次阶跃信号的幅值，单位 %'Unit:mN
 % 强制要求精度最高到0.001否则报错
   f_stepaFd = 7  ;    %——————————————————修改阶跃初始值
   f_stepbFd = 4 ;    %——————————————————修改阶跃终末值

 % 仿真总时间，单位S
 totalTime = 120; 

 % 人为给定阶跃信号的时刻，单位S
 stepActionTime = 60;

 % 仿真的控制步长时间长度，单位S
 % 100ms = 0.1S
 delta_t = 0.1;

 % 整个仿真过程的步进数为totalSteps
   totalSteps = totalTime/delta_t;
   tao = 10;  %单位秒S是阀门的时间常数
   flag = stepActionTime/delta_t;
 % 通过查表对比返回一个索引值对应的主流率大小
   mmfrNoa = find(subBestSchedule_2(:,1) == f_stepaFd);
   mmfr_stepaFd = subBestSchedule_2(mmfrNoa,2);
 % 循环产生第一阶段的实际模型主流率
 for j = 1:flag
mmfrN1(j)=(f_step0Fd)+(mmfr_stepaFd-(f_step0Fd))*(1-exp(-j*delta_t/tao));
 end
  % 通过查表对比返回一个索引值对应的主流率大小
   mmfrNob = find(subBestSchedule_2(:,1) == f_stepbFd);
   mmfr_stepbFd = subBestSchedule_2(mmfrNob,2);
 % 循环产生第二阶段的实际模型主流率
 for k =1:((totalTime-stepActionTime)/delta_t)
mmfrN2(k)= mmfr_stepaFd+(mmfr_stepbFd-mmfr_stepaFd)*(1-exp(-k*delta_t/tao));
 end
 %%把上面的两个主流率实际模型过程补在一起
   mmfrNN = [mmfrN1 mmfrN2];
 % 通过查表对比返回一个索引值对应的阳极电流大小
   IaNoa = find(fDemandToIa(:,1) == f_stepaFd);
   Ia_stepaFd = fDemandToIa(IaNoa,2);
   IaNob = find(fDemandToIa(:,1) == f_stepbFd);
   Ia_stepbFd = fDemandToIa(IaNob,2); 

 %%这里给模拟的传递函数中的固定参数赋值常量
         k1  = -42.6390869166903;
         k2  = -1.32483293227065;
         k3  = 0.200510429472484;
         k4  = -5.70516914317562;
         k5  = 37.163468956944;
         k6  = 2.95838142236669;
         k7  = 1.15327067269415;
         k8  = 0.6243246881009;

 % 产生两个数组
   stepActionTime_JieShu =((totalTime-stepActionTime)/delta_t);
 % zeros(m,n:);  %生成m*n的全0矩阵
   ia_a=ones(flag,1);
   ia_b=ones(stepActionTime_JieShu,1);
   ia_a=ia_a*Ia_stepaFd;
   ia_b=ia_b*Ia_stepbFd;
 % 把上面两个阶段的阳极电流矩阵拼接在一起
   ia =[ia_a ia_b];
 % ones(m,n) ;生成m*n的全1矩阵
   f_demand_a=ones(flag,1);
   f_demand_b=ones(stepActionTime_JieShu,1);
   f_demand_a=f_demand_a*f_stepaFd;
   f_demand_b=f_demand_b*f_stepbFd;
   f_demand = [f_demand_a f_demand_b];

 % 循环模拟每个控制周期
 % 初始情况下的实际推力和励磁电流应该为0
   im =zeros(totalSteps,1);
   ff =zeros(totalSteps,1);

for  i = 1: totalSteps

        ff(i) = k1 * (1 - exp(k2 * mmfrNN(i))) * im(i) * im(i) ...
                + (k3 * (mmfrNN(i) * ia(i)) * (mmfrNN(i) * ia(i)) + k4 * (mmfrNN(i) * ia(i)) + k5 * sqrt(mmfrNN(i) * ia(i)) + k6) * im(i)...
                + k7 * (1 - exp(k8 * mmfrNN(i)));

        im(i+1) = im(i) + pParameter*( f_demand(i) - ff(i) );
        if i == (totalSteps-1)
        break;
        end
 end

% 画图输出
% 用循环构造时间序列
for  j = 1:totalSteps
t(j) = j;
end

%%把推力的0.2倍幅值、主流率、励磁电流绘制在同一幅图里
%%
figure(2)
plot(t,ff*0.2,'b')   %推力函数值用蓝色
hold on  %MATLAB同一个figure里绘图保持命令
plot (t,mmfrNN,'r')  %主流率处理后用红色
plot(t,im*4,'g')       %闭环参数励磁电流用绿色
xlabel('时间 s');
ylabel('');
legend('推力','主流率','励磁电流');
title('主流率实际模型;推力×0.2显示;励磁电流×4')
grid on;   %打开网格

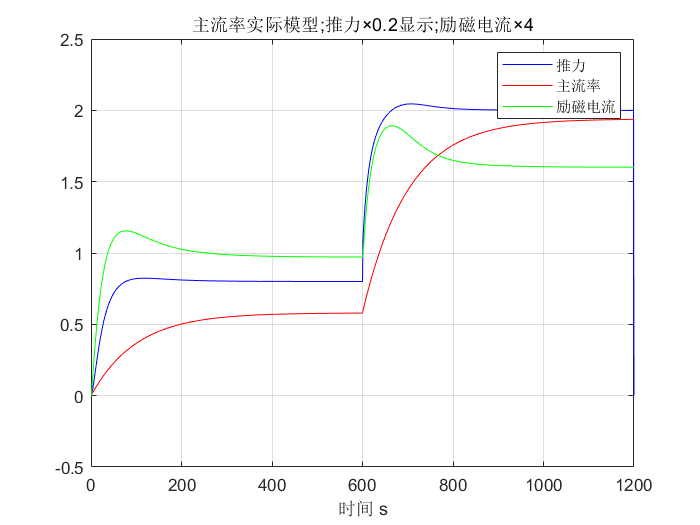
可以发现：实际仿真得到的推力蓝色线条的变化趋势和绿色的闭环反馈控制参数的变化趋势是一致的。