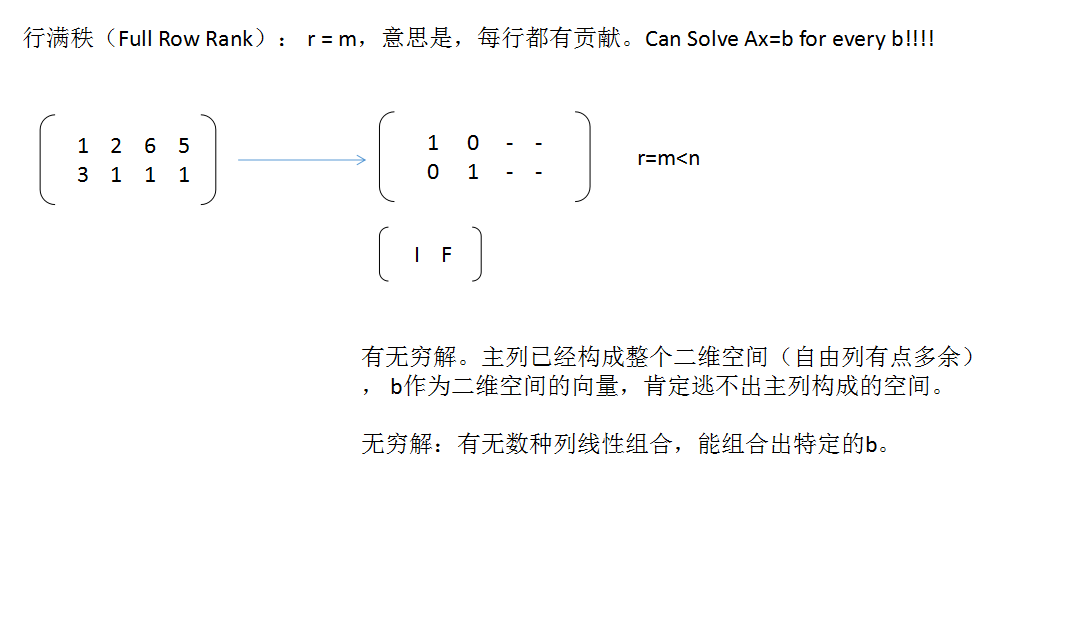
MIT线性代数：8.求解Ax=b，可解性和结构的更多相关文章

  1. 介绍求解AX=b:可解性与解的结构

    前面用高斯消元法或矩阵LU分解求解线性方程组的解,主要是针对有唯一解(矩阵A可逆)的情况,下面进一步介绍线性方程组有多个解的情况下,解的求解.

  2. 求解Ax=b

    一 线性方程组 Ax=b 的解释 线性方程组 Ax=b,其中矩阵 A 尺寸为 m*n, 当 A 为方正时,可使用消元法判断解是否存在并求解.当 A 为长方形矩阵时,同样可使用消元法判断解存在情况并求解 ...

  3. MIT线性代数：7.主变量，特解，求解AX=0

  4. MIT线性代数课程 总结与理解-第一部分

    概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...

  5. 线性代数笔记13——Ax=b的通解

    关于最简行阶梯矩阵和矩阵秩,可参考<线性代数笔记7——再看行列式与矩阵> 召唤一个方程Ax = b: 3个方程4个变量,方程组有无数解,现在要关注的是b1b2b3之间满足什么条件时方程组有 ...

  6. matlab 求解 Ax=B 时所用算法

    x = A\B; x = mldivide(A, B); matlab 在这里的求解与严格的数学意义是不同的, 如果 A 接近奇异,matlab 仍会给出合理的结果,但也会提示警告信息: 如果 A 为 ...

  7. python求解ax² + bx + c = 0

    系数需满足条件: a,b不能同时为0 b2-4ac≠0 代码如下def quadratic(a, b, c): """ 返回ax² + bx + c = 0的 " ...

  8. 【读书笔记】：MIT线性代数(5):Four fundamental subspaces

    At the beginning, the difference between rank and dimension: rank is a property for matrix, while di ...

  9. 【读书笔记】：MIT线性代数(3):Special Solution, Rank and RREF

    Special Solutions: Notice what is special about s 1 and S2. They have ones and zeros in the last two ...

随机推荐

  1. Win10 安装配置 MongoDB 4.0 踩坑记

    redis 官方没有 Windows 版的,微软维护的已经好久没更新了,所以就在想着换成 MongoDB. 于是一趟被我复杂化的踩坑之旅就开始了,同时也记录一下,避免有人遇见跟我一样的问题. 首先在  ...

  2. spring源码分析系列5:ApplicationContext的初始化与Bean生命周期

    回顾Bean与BeanDefinition的关系. BeanFactory容器. ApplicationContext上下文. 首先总结下: 开发人员定义Bean信息:分为XML形式定义:注解式定义 ...

  3. 搭建YUM本地仓库

    本文介绍如何利用CentOS 7 ISO光盘镜像搭建YUM本地仓库. 环境准备: (1)VMware15.5版本虚拟机 (2)CentOS-7-x86_64-DVD-1908光盘镜像文件 1. 搭建Y ...

  4. Android 列表(ListView、RecyclerView)不断刷新最佳实践

    本文微信公众号「AndroidTraveler」首发. 背景 在 Android 列表开发过程中,有时候我们的 Item 会有一些组件,比如倒计时.这类组件要求不断刷新,这个时候由于列表复用的机制,因 ...

  5. Ubuntu安装scrcpy手机投屏和控制(Ubuntu用QQ微信的另一种方法)

    Scrcpy 安装 snap install scrcpy adb服务安装 sudo apt-get install android-tools-adb adb配置 查看手机的USB识别号 手机通过U ...

  6. strcpy()、strncpy()和memcpy()对比

    strcpy()函数声明:char *strcpy(char *dest, const char *src)返回参数:指向最终的目标字符串 dest 的指针.注意事项:只能复制char类型的字符数组, ...

  7. 代码审计-EasyCMS

    cms来源AWD线下攻防平台题目.  链接:https://pan.baidu.com/s/1eUkyRspQmsv-0fIBby8ZlQ  提取码:tywa 失效可以联系我   0x01 文件上传漏 ...

  8. 爬虫3：html页面+webdriver模块+demo

    保密性好的网站,不能使用request请求页面信息,这样可以使用webdriver模块先开启一个浏览器,然后爬去信息,甚至还可以click等操作对页面操作,再爬取. demo 一般流程: 1)包含se ...

  9. opencv::模糊图像2

    中值滤波 统计排序滤波器 中值对椒盐噪声有很好的抑制作用 medianBlur(Mat src, Mat dest, ksize) 双边滤波 均值模糊无法克服边缘像素信息丢失缺陷.原因是均值滤波是基于 ...

  10. QuartzCode快速开发动画代码工具

    QuartzCode快速开发动画代码工具 QuartzCode一款快速,轻量,强大的动画工具,可快速得到原生的ObjC/Siwft代码 我可以用QuartzCode做什么? 应用程序演练动画 动画菜单 ...